基于贝叶斯网络理论的智能AGC设计

王鹤飞

(东北电力大学，吉林吉林132012)

0 引言

随着电力系统规模的不断扩大、其结构的改变和新兴的可再生能源的出现，以往那些有关AGC的设计对于现代电力系统来说不太适用。因此，应该在现代电力系统AGC的设计中应用一些智能控制技术。贝叶斯网络作为一种智能控制技术应用到现代电力系统中，能使AGC的设计有更强的自适应能力。贝叶斯网络的主要特征是通过给定一个能够影响结果的因素，将其对条件的依赖性加到模型中，进行智能判断。贝叶斯网络［1－2］是具有超强的记忆性，不受各种环境干扰因素的影响，能够很好地适应非线性的电力系统。贝叶斯网络模型之所以比其他的预测和记忆模型好，是因为它的神经结构网络能够清楚地表明其结构数据间的内在联系。因此，本文主要阐述基于贝叶斯网络理论的AGC的设计，及其应用于计及风机并网的现代互联电力系统。同时，提出了一种贝叶斯网络系统的构架。

1 贝叶斯网络的基本原理

1.1 网络图模型

该模型的基本思想是建立模块化概念，即复杂的系统都是由许多简单的个体部分联合而成的。网络图模型的理论思想是图论和概率论的密切结合的产物。概率论是提供了组合这些模块的黏合剂，并同时为有关数据和模型提供了连接的界面。图模型中的图论部分，不仅提供了相互影响变量集的直观界面，而且提供了有效算法的数据结构［3］。

概率图模型中的图的节点代表随机变量，边代表变量之间的概率联系。如果两个节点之间没有边相连，它们是独立的变量，否则它们是因变量。该模型还提供了变量间的联合概率分布。例如，有n个二进制的随机变量，它们的联合概率为P(x1，…，xn)，需要O(2n)个参数表示，而通过图模型，根据相关性的假设，则可以指数倍地减少参数的个数，有利于模型后续的推导和记忆性的学习。

现有两种主要的图模型:有向图模型和无向图模型。无向图模型也被称为马尔科夫网络或者马尔科夫随机场，这种网络广泛地应用于物理界;有向图模型被称为贝叶斯网络、可信度网络或生成模型，广泛地应用于人工智能等领域。这种模型中A、B连个节点由有向弧连接，且A指向B，A形象地被称为父亲节点，B为孩子节点。

1.2 贝叶斯网络

贝叶斯网络(BN)具有强大的记忆功能，能够处理网络中大量节点间的联系问题，这种模型能够对大量的服从联合概率分布的变量进行编码［4］。

BN还被广泛地应用在人工智能领域，并成为了系统构建的标准方法。

BN由n个随机变量组成，每个变量代表一个网络节点，它们之间的联系用有向弧表示，通常表示起因的节点指向结果的节点，这样就可以在各个节点之间画出它们的关系，并且用概率表示节点间的影响程度。条件概率表(CPT)为各变量均指定了条件概率。

网络中的节点和随机变量间是一对一联系的。BN结构中，将每个节点及其所代表的变量用xi表示，pai代表节点xi的父亲节点(即对xi施加影响作用的那些节点，是用有向弧表示其施加影响和方向的)。这样对所有变量集的联合概率分布可表示为

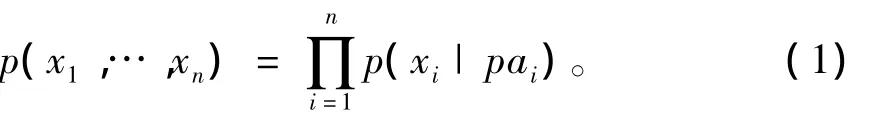
有关贝叶斯网络结构的基本任务是:构建学习阶段:找到图形模型构架;参数学习阶段:找到节点概率分布;贝叶斯网络的推理阶段是在已知观察变量集合e条件下，估计查询变量q的后验概率分布p(q|e)。应用不同类别的算法来估计边际后验概率p(x|e)。

推理也是一种具有概率性的行为，贝叶斯网络的优点是可以通过推理出先验概率的分布，进而获得查询概率的分布。

2 电力系统三控制区域的算例

用IEEE的10机39节点的升级算例为例，并将其分为3个控制区域，和MARL系统［5］计算的结果相比较。

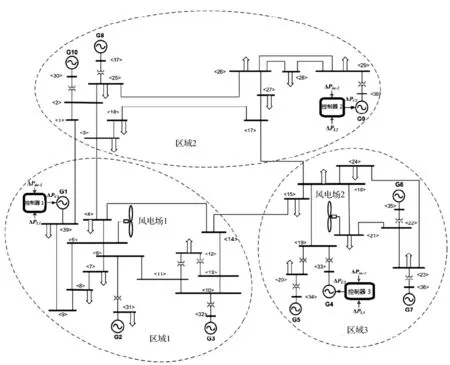
图1 IEEE的10机39节点系统

图1给出了系统算例接线图。该系统中有10台发电机、19个负荷、34条电力传输线和2台变压器。系统中的区域1和区域3都加了风电场，3个区域总的装机容量为841.2 MW，其中风电装机容量为45.34 MW。区域1中的总的装机容量为198.96 MW，其中风电装机容量为22.67 MW，负荷为265.25 MW;区域2的总装机容量为232.83 MW，负荷也为232.83 MW;区域3的总装机容量为160.05 MW，风电装机容量为22.67 MW，负荷为124.78 MW。

该测试系统所需的仿真参数如发电机、负荷、电力传输线和变压器等已在文献［5］中给出。系统中所有的电厂均配备有调速器和电力系统稳压器(PSS)，而且每个区域中只有一台承担AGC调频任务的发电机，即G1、G9和G4。

系统中还有3台智能控制器，用于在适当的时候为系统供给电力。

在控制区域内伴随有负荷的扰动，相应的控制区域的频率也会经历一个暂态的变化，这时区域的反馈机制将会给参与调频的机组一个增发或减发的信号，进而各个机组根据它们的优先顺序进行发电，确保发电侧和负荷侧平衡。在电力系统稳定状态下，发电侧和负荷侧是相对稳定的，使得联络线功率偏差和频率偏差均为零。而控制信号却是按在某控制区域中的发电机的数量进行分配的［6］。

由于风电的大规模使用和其独有的动态特性，例如有较大的动能。风电机组的地位要比其他的可再生能源更加重要［7］。

3 控制策略

针对系统中的AGC问题，本文所提出的贝叶斯网络模型主要有以下几点优点:模型的建立是以电网络拓扑结构为基础的;可以很容易的兼顾频率响应模型的不确定性和其独立性;能够对整个系统中的变量进行很好地监测;在传输概率信息时，允许大量的假设分析;电力系统中的参数值具有相对独立性。

在学习阶段，系统中所有重要的参数是:Δptie、ΔpL、Δf、ACE 和 Δpc。

为了找到相对合适的训练数据集，用调谐PI控制器对模型进行了100 s仿真。每进行100 s的仿真，都会得出训练数据矩阵的其中一行。和每个区域变量有关联的训练数据，并被传到控制器中，当与贝叶斯网络列表中的数据不符时，控制器将会把输入的数据数字化，然后传到贝叶斯列表中。在贝叶斯列表中能够找到和每个区域的图形模型变量相关的条件概率分布值。

在完成学习阶段后，进入推理阶段，每一个仿真步长时间内，区域控制器将获得输入的模型参数，利用贝叶斯网络工具箱(BNT)估计后验概率分布，最后控制器输出Δpc。

3.1 控制器构架

传统的AGC使用的是比例积分控制器(PI控制器)。本段将介绍一种智能控制方法，该方法将贝叶斯网络的技术应用于集成了风机的控制器上。此设计的控制目标是控制带有风力发电机的电力系统的频率在允许的波动范围内，以求达到期望的控制性能。所得的结果将与文献［5］［8］提出的MARL控制设计方法相比较。

图2表示的是一台智能的控制器，该控制器是用来对电力系统进行适当的补偿的。

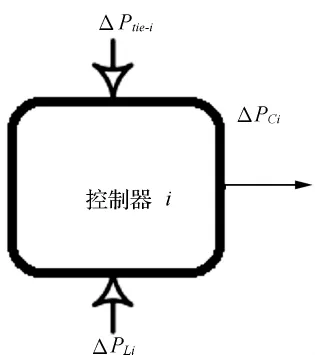
图2 第i区域的模型

3.2 构建贝叶斯网络

为了说明贝叶斯网络的构建过程，首先要确定模型中的几个重要的变量。初始的任务并不是那么直观明了，以下四点是总任务的一部分:

a.确定模型的目标。

b.确定和待解决的问题相关的观察变量值。

c.确定和模型直接相关的观测值。

d.将观察到的值赋予那些处于互斥状态的变量中。

在该方法中利用补偿控制手段将ACE值尽快地归零。后验概率分布中的查询变量为Δpc，其和待解决问题相关的观测值的后验概率分布如下:

根据式(2)可以得出，有许多和待解决的问题相关的观测变量值，其中和模型参数联系最大的是频率偏移因素。负荷扰动和联络线功率偏移是造成频率偏移和ACE值变化的主要原因。其合理的后验概率分布表达式是 p(Δpc|Δptie，ΔpL)。Δptie值是可以通过实际的测量得到的，ΔpL的值是输入参数中不能直接测量的，但是可以用数值分析的方法估计到。在文献［7］中讲述了一种能够很好地预测估计负荷扰动量的方法。然而，这种方法依赖于频率的梯度和某种特定的系统参数。此外，就AGC在电力系统中的职责而言，估计过程所经历的时间是无关紧要的。

3.3 贝叶斯网络学习的过程

在确定最合理的观测值Δptie和ΔpL后，建设贝叶斯网络的下一个阶段是构造一个有向开环图，该图涉及到待求问题的随机变量、节点条件概率分布以及节点间的联系，如图3所示。根据式(3)可知，ACE值和频率偏移(Δf)、联络线功率偏差(Δptie)密切相关，所以Δptie和Δf是贝叶斯网络图模型中ACE的父亲节点;而频率偏移又和负荷扰动(ΔpL)、联络线功率偏差相关，因此，它们又是Δf的父节点。

Δpc与ACE值有关，因此，ACE节点是控制信号的父节点。

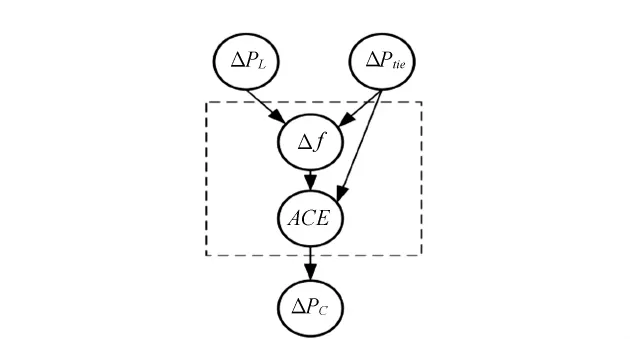
图3 区域的图模型

根据联合概率分布，得出:

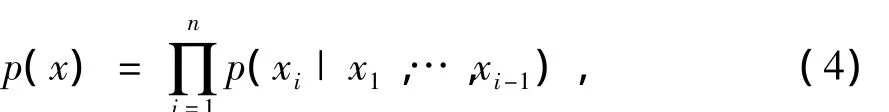
x1，…，xi－1是 πi的子集，即 πi⊆(x1，…，xi－1);且变量之间相互条件独立，进而能够得出:

联立式(4)和式(5)可得:

将式(4)和式(6)比较，π1，…，πn和 BNS的父亲节点pa1，…，pan相对应，进而能够确定网络结构S中的有向弧，最后确定一个贝叶斯网络构架。

由式(5)可知，有条件的依赖关系如下:

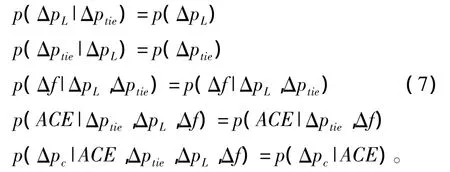
贝叶斯网络学习阶段结束后，根据训练数据得出条件概率分布p(xi|pai)。然而，问题的关键是要求出式(7)中等式右边的概率分布和条件概率分布值。

利用贝叶斯网络工具箱(BNT)对模型进行概率推理，BNT利用训练数据矩阵，并找出和图形模型变量相关的条件概率分布。

3.4 贝叶斯网络推理

从先验概率分布的数据可以确定贝叶斯网络，进而得到模型中变量的概率分布，给出观察变量值估计查询变量的后验概率分布，即 p(Δpc|Δptie，ΔpL)。但这个概率分布并不是模型所固有的，而是经过估计得到的。

4 仿真结果

为了论证本文所提出的控制设计的有效性，将模型进行了相应的仿真。做一个测试，将负荷扰动加入这3个控制区域中。区域1中的母线8、区域2中的母线3和区域3中的母线16的负荷都有所增加，其值分别为总区域负荷的 3.8%、4.3%和6.4%，3个区域频率偏差(Δf)、区域控制偏差(ACE)的波形曲线如图4、图5和图6所示。

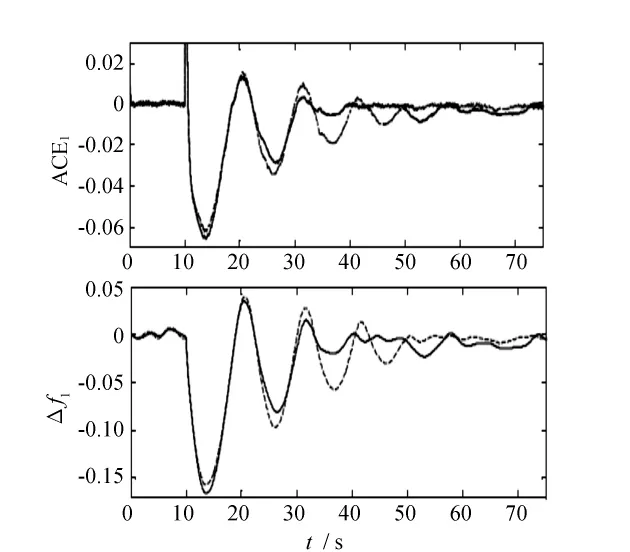
图4 区域1响应;所提出的多机贝叶斯网络的方法(实线表示)和MARL方法比较(虚线表示)

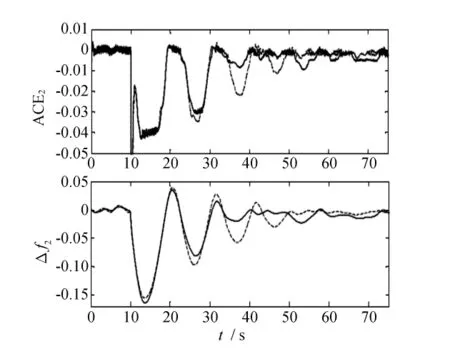
图5 区域2响应;所提出的多机贝叶斯网络的方法(实线表示)和MARL方法比较(虚线表示)

图6 区域3响应;所提出的多机贝叶斯网络的方法(实线表示)和MARL方法比较(虚线表示)

将风场模型(不含低通滤波器)加入10机39节点系统中，对模型进行仿真，看看风机对整个电力系统频率的影响。结果表明电力系统的频率在很大的程度上受风电波动的影响。在图4、图5和图6中，只是记录了一个暂态的信号(ACE和Δf)过程。其实，风电场作为电力系统的一部分，对电力系统的频率产生较大的影响，那是因为风力发电的预测值和实际值的偏差较大造成的。

仿真结果表明，在较大的负荷波动和风力发电的随机性下，本文所提的方法能够使ACE和Δf值迅速归零，而且所用的智能控制器起信号平滑作用，使得Δf值减小(较MARL方法设计的控制器)。

5 结论

将基于大规模电力系统的多机贝叶斯网络AGC的设计方法应用于3区域的电力系统进行测试，并与MARL方法所得的结果相比较，得出此方法能够使得ACE和值迅速归零，而且，对于联合电力系统的稳定起到了至关重要的作用。

［1］张连文，郭海鹏.贝叶斯网引论［M］.北京:科学出版社，2006:100－148.

［2］华鹏.贝叶斯决策及分析若干问题的研究［D］.青岛:山东科技大学，2004:1－51.

［3］JORDAN M.An introduction to graphical models［Z］，2001.

［4］高汝召.贝叶斯决策理论方法的研究［D］.青岛:山东科技大学，2006.

［5］BEVRANI H，DANESHFAR F，DANESHMAND P R.Intelligent power system frequency regulation concerning the integration of wind power units［M］.［S.l.］:springer press，2010:120 －165.

［6］BEVRANI H，HIYAMA T.On load– frequency regulation with time delays:design and Real－ Time implementation［J］.Energy Conversion，IEEE Transactions on，2009，24(1):292－300.

［7］HASSAN B.Robust power system frequency control［M］.New York:Springer，2009:100 －135.

［8］DANESHFAR F，BEVRANI H.Load－frequency control:a GA－ based multi－ agent reinforcement learning［J］.Generation，Transmission＆ Distribution，IET，2010，4(1):13－26.