带转换层高层建筑分段隔震体被动控制参数优化

高剑平，罗 丹，潘月月

（华东交通大学土木建筑学院，江西南昌330013）

近年来，国内外高层建筑得到了迅速发展，逐渐向着体型复杂、功能多样的方向前进。为了满足建筑功能布局的需要，常需设置一个或多个转换层，这类建筑已成为现代高层建筑发展的一大趋势。然而，带转换层的复杂高层建筑，由于竖向构件不连续，导致转换层附近易产生刚度、内力和传力路径突变，转换层上、下楼层的构件受力十分复杂，难以达到抗震需求[1]。转换结构设计十分困难。由于地震的强随机性，单纯依靠传统的体系和方法设计这类建筑，结构安全难以保证。即使幸免于倒塌，震后结构本身往往损伤严重，不仅造成重大经济损失和人员伤亡，并且修复极为困难或者需付出高昂的代价。因此，寻求新的耐震结构体系和设计概念不失为一条可行的解决途径。

1 分段隔震体系的技术来源和基本原理

许多中外古建筑历经上千年地震灾害的考验，安然无恙，其中蕴涵的防震措施与现代先进的隔震、减震、控振技术暗合，其技术措施具有很高的借鉴价值，可为现代结构“抗震”研究开拓思路。

久负盛名的日本五重塔，在地震不断的日本，经1 400余年，历史上还没有它们倒塌的记录[2-3]。相对于现代建筑在地震中损毁、倒塌严重，日本古塔的抗倒塌能力是一个奇迹。这应该归功于其独特的结构设计。塔的每层与相邻层之间没有任何连结，塔各层只是像帽子一样摞在一起，起连接作用的是各层地板之间配合得相当宽松的木支架，它们保证了木塔各层之间的自由滑动。从旁边看，在外力作用下的木塔仿佛在跳一种“蛇形舞”（snake dance）[3]，如图1所示，使得每层的运动方向与邻层相反，惯性力相互抵消，通过各层之间的相互滑动耗散地震能量。

图1 “蛇形舞”示意图Fig.1 Diagram of the snake dance

武田寿一[4]对日本古代木构建筑抗震机理总结道：“五重塔采用的并不是狭义的基础隔震结构，而是将结构长周期化并可巧妙传递地震力，从这个意义上说，五重塔也是一种隔震结构。”迄今为止，对五重塔的耐震机理之说[2]仍然没有穷尽，是一个值得深入研究的课题。

无独有偶，中国古代的石经幢，如赵州陀罗尼经幢（见图2）和多层阁塔、殿堂[5]，古希腊帕提农神庙的鼓状柱[6]（见图3），都利用“刚体叠置”，使石结构或木结构变成“柔性结构”，并辅以摩擦阻尼或金属阻尼来耗能，在这一点上中西方智慧不谋而合。其实，许多西方学者很早就注意到中国古建筑宽大低矮、结构分层具有抗震意图（见图4）。现代研究[6]表明：辅作层是典型的耗能结构层，发生地震时，该层将会消耗大量地震能量，大大衰减结构的地震响应，使结构减轻甚至免于破坏。

图2 赵州陀罗尼经幢Fig.2 Dharani Stambhas in Zhaozhou city，Heibei Province，China

图3 古希腊帕提农神庙的鼓状柱Fig.3 Drum-shaped columns in ancient Greek Parthenon

总之，上述中外著名古建筑的构建思想可以简单概括为“刚体叠置”。其抗震技术可以概括为：刚体叠置，柱底磨擦滑移隔震；控制高宽比防倾覆；层间大摩擦防错移。当然，它们优异的耐震性能是多种减震耗能机制的综合，其中“刚体叠置”是实现耐震的主要技术措施之一。

针对带转换层复杂高层建筑抗震性能较差的缺点，受中外著名古建筑优异的耐震性能的启发，另辟蹊径，提出一种新型的隔震结构体系。该体系是在上、下体系转换和/或柱网轴线转换部位设置隔震层，同时，结构下部采用基础隔震，隔震层可由铅芯橡胶支座和位移相关型阻尼器组成，形成“刚体叠置”，如图5所示，可称之为“分段隔震体系”。

图4 殿堂结构木构架分层示意图Fig.4 Hierarchic structure of Chinese ancient timber temple

图5 带转换层复杂高层建筑分段隔震体系示意图Fig.5 Diagram of segmented isolation for complex high-rise building with transfer story

该体系通过隔震层将高层建筑分割为若干个高宽比较小的“子结构”，将原来“刚性”的抗震结构体系变成“刚柔相济”的分段隔震体系。并且，各个“子结构”作近似刚体的水平运动，这样避免了原来高柔结构的弯曲变形，倾覆稳定问题也迎刃而解。

该体系象多个基础隔震结构竖向叠置在一起，通过“刚体”之间的相对运动来换取主体结构构件本身的小变形，这样可以有效地减少主体结构的损伤。同时，“刚体”之间的大错移可以带动隔震层的变形，通过隔震层的大阻尼特性来消耗输入的地震能量，削减地震响应。

也可以认为隔震层是有意识设置在竖向刚度突变位置的薄弱层，将地震输入到结构的能量引入到这些特别设置的耗能层中，来实现能量的吸收和集中耗散，以保护主体结构的安全，从而实现主体结构“无损”或“免修”的最高损伤控制目标，而且，震后这些部位也容易修复或更换，具有显著的经济优势和社会效益。

2 基于能量的分段隔震结构被动控制参数分析方法

从形式上看，分段隔震结构是糅合了基础隔震和层间隔震的一种体系，兼具二者的某些特征和优点，但由于隔震层设置位置和数量的不同，其减震机理、振动特性、地震响应规律等诸多方面有别于基础隔震结构和层间隔震结构，可能出现一系列新的特性。因此，研究从随机振动理论和能量平衡原理出发，选用杜修力[7]过滤白噪声模型模拟平稳地震动随机模型，并采用Bouc-Wen滞回恢复力模型对分段隔震结构中隔震层的非线性系数进行了等效线性化，建立了分段隔震结构基于能量的被动控制参数分析方法。通过进行参数分析和能量分析来获得分段隔震结构体系的最优参数组合及能量响应规律。

2.1 目标函数

减轻或控制结构地震反应的基本原则是以适当的方式消耗地震输入的能量，研究对分段隔震结构两自由度体系被动控制参数优化分析以隔震层滞回耗能期望占输入结构总能量期望的比值最大为目标函数，以隔震层上下结构的质量比、频率比以及隔震层的屈服后刚度比和阻尼比为控制参数，隔震层位移为约束条件对结构进行参数分析，其方法可以归纳如下

式中：δmj为基础隔震层和中间隔震层的最大允许层间位移；E[]为取期望；Ed，Ein为隔震层滞回耗能和地震总输入能量；m1，m2为为主体结构Ⅰ和结构Ⅱ的等效质量；k1，k2为基础隔震层和中间隔震层的水平刚度；x1，ẋ1，ẍ1为结构Ⅰ与基础面之间的相对位移，速度和加速度；x2，ẋ2，ẍ2为结构Ⅱ与结构Ⅰ之间的相对位移，速度和加速度；xg，ẋg，ẍg为地面水平地震位移，速度和加速度；γ1，γ2为基础隔震层和中间隔震层屈服后与屈服前的刚度比；z1，z2为基础隔震层和中间隔震层的滞变位移；t为时间；j为子结构编号；s.t.为约束条件。

1.2 Bouc-Wen滞回恢复力模型

由于地震激励的强随机性，分段隔震结构在地震强干扰下会进入弹塑性状态，表现出滞回特性。因此，本文采用Bouc-Wen模型作为隔震层的恢复力模型，对隔震层进行等价线性化。Bouc-Wen恢复力模型中，刚度的突变能够较为真实的反映系统的屈服特性，虽然该模型不完全符合塑性理论，但是其滞回环光滑多变，并且能量计算方便，在工程中应用广泛。其恢复力模型的方程[8]表示如下

其中

并设

式中：f是关于 x，ẋ，z的函数；A，n，α，β，γ都是滞回常数；x和 z分别为位移和滞变位移；A，α，β控制滞回曲线的比例和形状；n控制滞回曲线的光滑程度，一般地，取n=1；Ce，Ke为等效线性化参数；ż，ẋ分别为对z和x的求导。

2.3 地震地面运动的随机模型

实际地震记录地震动的统计特性表明，地震动是非平稳过程，但是在工程应用中为了简化问题和方便分析，通常不考虑频率非平稳性。本文采用杜修力-陈厚群[7]提出的零均值平稳过滤白噪声模型，该模型以一种基岩地震动为有色谱的随机地震动模型，能较好的反映实际地震动的谱函数，其功率谱函数为

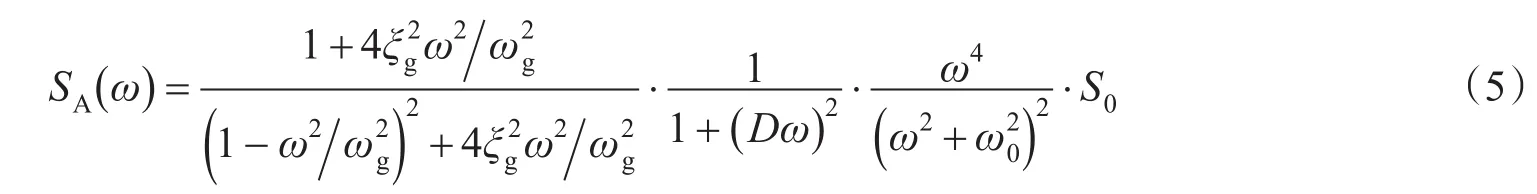
式中：D，ω0为与地震震级有关的谱参数，高频减量D可取为1 28π，低频减量ω0可取为1.83；ξg为地表土层阻尼比；ωg为地表土层的卓越频率；S0为随机机率谱密度；ω为地震震动频率。

2.4 分段隔震结构动力分析模型和运动方程

分段隔震结构中将主体结构看作刚体，并对分段隔震结构作如下假定：上部结构仅考虑水平整体位移，认为结构完全对称不考虑摆动式扭转的影响；结构的水平位移主要集中在基础隔震层和中间隔震层上；用隔震层的刚度和阻尼近似代表结构体系的刚度和阻尼。基于以上假定，分段隔震结构可以简化为一个两质点的隔震结构动力分析模型，如图6所示。图6 分段隔震结构动力分析模型

Fig.6 Dynamic analysis model of segmented isolation

该计算模型的非线性运动方程为

式中：c1，c2分别为基础隔震层和中间隔震层的阻尼系数。

体系平稳状态矢量X()t的二阶中心矩R(t)满足如下方程

3 算例参数分析

研究采用一个40层的高层建筑算例进行分段隔震结构基于能量的参数优化分析，假定该高层建筑的质量和刚度沿高度方向均匀变化，其一次固有周期为5.0 s，各层层高为4.0 m，质量为106kg。该高层建筑结构所在的场地条件为：位于Ⅱ类场地土，地震烈度为9度，设计地震分组为第一组，则ξg=0.72，ωg=17.95 rad⋅s-1，S0=23.585 9 cm2⋅s-3。通过构造结构的第一层与中间层的i层为隔震层的方法对各参数进行分析，以研究隔震层参数对分段隔震结构位移和能量相应的影响规律。

表1 隔震层质量比μ取值Tab.1 Mass ratio of the isolation layers

如表1所示，设定中间第34层、25层、20层和14层分别为中间隔震层，质量比的大小随中间隔震层位置的下移而增大。两隔震层的屈服前后刚度比rj均在0.100～0.600范围内取值，两隔震层的阻尼比hj均在0.100～0.300范围内取值，隔震层位移要求满足：x1，x2≤ 10 cm 。

3.1 质量比的影响

为了便于分析质量比的影响，本小节中假设两隔震层的屈服后刚度比和阻尼比相同。并且，对应于四个质量比，研究两隔震层位移方差、能量比值及频率比η分别与隔震层屈服后刚度比rj和隔震层阻尼比hj及频率比的关系时，假定两隔震层的屈服后刚度比或阻尼比取值为0.100。隔震层位移方差的单位为cm。

图7 基础隔震层位移方差Fig.7 The base isolation layer displacement variance

图8 中间隔震层位移方差Fig.8 Displacement variance the intermediate isolation layer

图9 隔震层滞回耗能占地震总输入能量的比值Fig.9 Ratio of the hysteretic energy in the total seismic energy

3.1.1 质量比为0.176

由图7、图8、图9可知，质量比为0.176时，基础隔震层的位移方差，随着频率比的增大而增大；随着隔震层屈服后刚度比的增大而减小。比较图7（a）和7（b）可得，随着隔震层的阻尼比的增大，基础隔震层位移方差减小的趋势不断减缓。中间隔震层的位移方差，随着频率比的增大而减小，随着隔震层屈服后刚度比的增大先减小后增大，随着隔震层阻尼比的增大而减小。隔震层滞回耗能占地震总输入能量比值随着隔震层屈服后刚度比和阻尼比的增大而减小，而受频率比的影响不明显。

3.1.2 质量比为0.600

与质量比为0.176时相比，质量比为0.600时基础隔震层的位移方差最大值明显减小，且随着隔震层屈服后刚度比的增大逐渐由不断减小变为先减小后增大。而隔震层的滞回耗能与地震总输入能量的最大比值增大了，在隔震层屈服后刚度比和阻尼比一定的情况下，存在最优频率比使得隔震层的滞回耗能占地震总输入能量的比值最大，而且隔震层阻尼比曲线对应的最优频率比值较大。

3.1.3 质量比为1.000

质量比为1.000时，隔震层屈服后刚度比和阻尼比对两隔震层位移方差的影响逐渐减小，而受频率比的影响则逐渐增大。隔震层滞回耗能占地震总输入能量的最大比值较质量比为0.600时的最大比值有所减小，而且最优频率比也小于质量比为0.600时的最优频率比。

3.1.4 质量比为1.857

质量比为1.857时，隔震层屈服后刚度比和阻尼比对两隔震层位移方差的影响继续减小，且基础隔震层的位移方差最大值也不断减小，而中间隔震层的最大位移方差始终保持在10 cm附近，可见中间隔震层的减震效果优于基础隔震层的减震效果。隔震层的滞回耗能占地震总输入能量的比值最大值虽然较质量比为1.000时的最大比值有所增大，但是仍小于质量比为0.600时比值的最大值。

3.2 频率比最优时质量比对能量比值的影响

图10表明，隔震滞回耗能与地震总输入能量的最大比值对应的最优频率比随质量比的增大而减小，在质量比较大时，最优频率比减小的幅度很小，分段隔震结构在质量比较大时主要通过延长其自振周期而减震。由图11（a）可知，质量比在0.176～1.000范围内时，隔震层滞回耗能占地震总输入能量的比值随质量比的增大先增大后减小，在质量比为0.600时比值最大；当质量比大于1.000时，隔震层的滞回耗能占地震总输入能量的最大比值有所增大，但仍小于0.600时最大的比值。这表明，中间隔震层的位置对分段隔震结构的减震效果有一定的影响，当中间隔震层位于分段隔震结构的中部时，隔震滞回耗能占地震总输入能量的比值最大。图11（b）中，随着隔震层阻尼比的增大，隔震层的滞回耗能占地震总输入能量的最大比值对应的质量比有所减小，但是中间隔震层的位置仍然在高层建筑结构的中部。

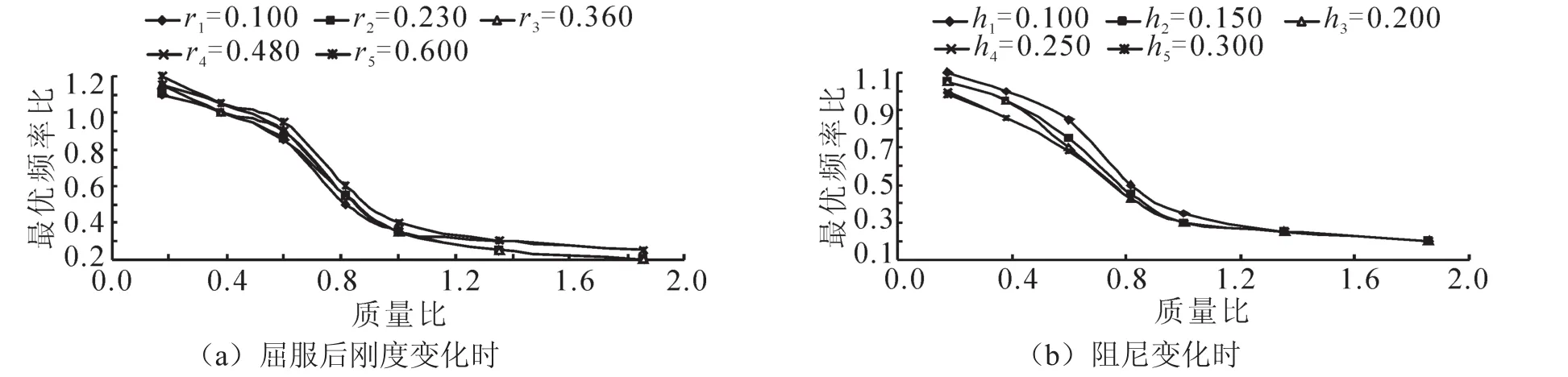
图10 最优频率比Fig.10 Optimal frequency ration

图11 隔震层滞回耗能占地震总输入能量的比值Fig.11 Ratio of the hysteretic energy in the total seismic energy

3.3 质量比最优时隔震层屈服后刚度比和阻尼比对能量比值的影响

由图12可得，两隔震层屈服后刚度比和阻尼比对隔震层滞回耗能占地震总输入能量的比值影响主要表现为：随着两隔震层屈服后刚度比和阻尼比的增大大，能量比值单调减小。

图12 隔震层滞回耗能占地震总输入能量的比值Fig.12 Ratio of the hysteretic energy in total seismic energy

4 结论

1）质量比的大小取决于中间隔震层的位置，当中间隔震层位于结构的中部附近时，隔震层滞回耗能占地震总输入能量的比值最大。

2）屈服后刚度比及阻尼比一定时，对应于不同质量比存在最优频率比使得隔震层的滞回耗能占地震总输入能量的比值最大，并且此最优频率比随质量比的增大而减小，且在质量比较大时减小值较小。而且随着质量比的增大，隔震层的屈服后刚度比和阻尼比对两隔震层位移方差的影响减弱。这表明，质量比较小时，结构主要通过改变隔震层的频率比来减震；随着质量比的增大，结构逐渐成为通过改变隔震层的频率比和延长结构的自振周期来共同减震；当质量比增大到一定值时，结构基本成为依靠延长结构自振周期减震。可见，在分段隔震结构设计中，质量比的确定会直接影响整个隔震结构的减震效果。

3）质量比一定时，随着频率比的增大，两隔震层的位移方差随着频率比的增大而不断减小，随着隔震层屈服后刚度比的增大先减小后增大，随着隔震层阻尼比的增大而减小；隔震层滞回耗能占地震总输入能量比值随两隔震层屈服后刚度比和阻尼比的增大而单调减小。

4）两隔震层屈服后刚度和阻尼比一定时，随着质量比的增大，基础隔震层的位移方差最大值不断减小，而中间隔震层的位移方差最大值则始终保持在规定的隔震层位移限值附近，因此，基础隔震层位移方差的改变对分段隔震结构的减震效果具有较大的影响。

[1]唐兴荣.特殊和复杂高层建筑结构设计[M].北京：机械工业出版社，2006.

[2]周福霖.工程结构减震控制[M].北京：地震出版社，1997.

[3] KOJI NAKAHARA.Earthquake response of ancient five-story pagoda structure of horyu-ji temple in japan[J].12th World Conference On Earthquake Engineering，2000（11）：1-6.

[4]武田寿一.建筑隔震防震与控制[M].纪晓慧译.北京：中国建筑工业出版社，1997.

[5] DIMITRIOS KONSTANTINIDIS，NICOS MAKRIS.Seismic response analysis of multidrum columns[J].Journal of Earthquake Engineering and Structural Dynamics，2005，34（10）：1243-1270.

[6]高大峰，赵鸿铁，薛建阳，等.中国古代木构建筑抗震机理及抗震加固效果的实验研究[J].世界地震工程，2003，19（2）：1-10。

[7]党育，杜永峰，李慧，等.基础隔震结构的耗能分析[J].世界地震工程，2005，21（3）：100-104.

[8]杜修力，胡晓，陈原群.强震地运动随机过程模拟[J].地震学报，1995，17（1）：103-109.