矩阵式变换器空间矢量调制谐波的分析及仿真*
2011-08-16刘元度
李 孟,任 杰,刘元度
(西安飞行自动控制研究所机电中心,西安 710065)
矩阵式变换器是一种直接变换型交流-交流电力变换装置,具有优于传统脉宽调制PWM(pulse width modulation)变频器的特性:能量双向流通、正弦输入与输出电流、可控的输入功率因数、输出电压幅值和频率均可独立调节,没有中间直流环节,体积小、重量轻、可靠性高等。由于这些优点,使它在交流电机调速领域中具有广阔的应用前景。因而在交流调速系统中,使用矩阵式变换器驱动电动机,一方面能够实现较好的传动性能,另一方面也可以满足日益严格的电网电能质量的要求[1]。
矩阵式变换器包含开关多,数学模型复杂,控制烦琐。因此,实际应用中,采用理想的调制策略,在保证输出电压质量的条件下,使系统能够稳定可靠地运行,是一个至关重要的问题。从20世纪80年代出现矩阵式变换器雏形以来,国际上主要流行着三类调制策略:直接传递函数法、空间矢量调制法和双电压控制法,并取得较好的效果。为了进一步简化调制方法,改善输入输出波形,学者们仍致力于研究更加新颖的调制方法。
1 矩阵式变换器基本拓扑结构及原理
矩阵式变换器是一种含有m×n个双向开关的单级电力变换器,可以将输入侧m相电压源直接连接至n相负载。而常用的是三相-三相交流矩阵式变换器,包括3×3共9个双向开关Sij(i=A,B,C;j=a,b,c)。每个双向开关都具有双向导通和关断的能力。三相-三相交流矩阵式变换器拓扑结构如图1所示。
通过9个双向开关的有序开断,把变换器输入端的恒幅、恒频电压,转变为幅值和频率可以任意改变的电压,供负载使用。双向开关的有序开断技术,也称为调制策略。空间矢量调制法是矩阵式变换器的主要调制策略之一。下面着重介绍空间矢量调制方法。
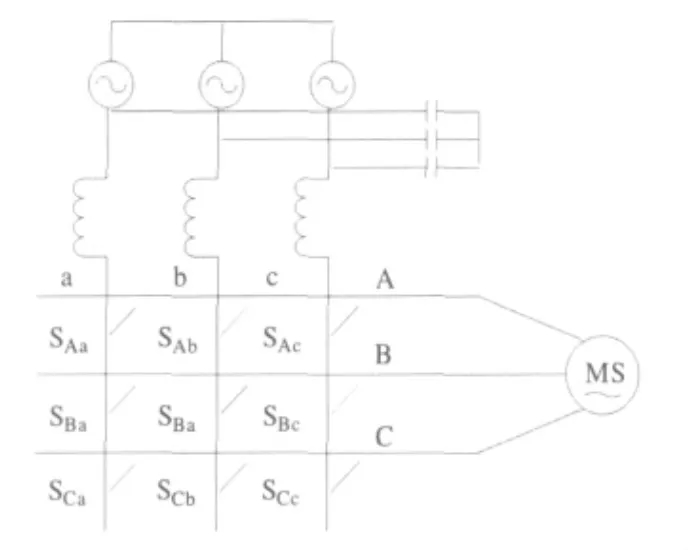
图1 矩阵式变换器拓扑结构Fig.1 Topology of matrix converter
2 矩阵式变换器空间矢量调制基本原理
空间矢量调制法包括间接空间矢量调制法和直接空间矢量调制法。虽然间接空间矢量调制法与直接空间矢量调制法建立的模型不同,但是基本算法都是建立在空间矢量调制的原理上。可以证明,两种调制算法的结果是相同的。也就是说,两种调制过程和输出(输入)端所包含的谐波是一样的。但是,间接空间矢量调制法更直观,更易于理解,因此,本文以间接空间矢量调制法为例,来说明这种调制策略的基本原理和特定谐波的定量分析。
间接空间矢量调制方法是将矩阵式变换器等效为交-直-交结构,如图2所示。
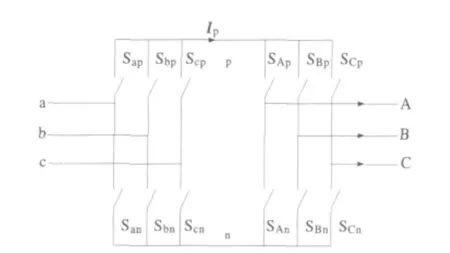
图2 矩阵式变换器等效交-直-交结构Fig.2 AC-DC-AC structure of matrix converter
其中有一个虚拟的直流环节p-n,直流环节的左半部分为交-直部分,即虚拟整流部分,右半部份为直-交部分即虚拟逆变部分。经典的空间矢量脉宽调制技术就可以分别应用到虚拟整流器和虚拟逆变器上,从而实现对矩阵式变换器的调制[4~6]。
2.1 虚拟逆变器输出线电压空间矢量调制
根据空间矢量调制原理,矩阵式变换器输出线电压空间矢量可以定义为
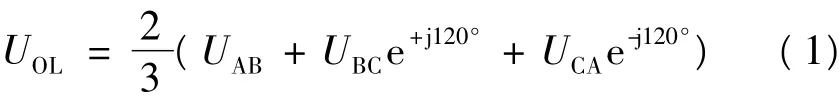
在虚拟逆变器部分,由于矩阵式变换器的输出相不能断路,所以必须满足同一输出相上有且只有一个开关导通。虚拟逆变器的6个开关管共有8种可能组合,分别为6个长度均为V的静止非零空间矢量和2个零矢量,如图3所示,6个静止的非零空间矢量将平面平均分为6个扇区,括号中的符号表示空间矢量对应的开关状态,开关与正极接通表示为p,与负极接通表示为n,uAB、uBC、uCA为旋转的空间矢量的三相坐标轴。
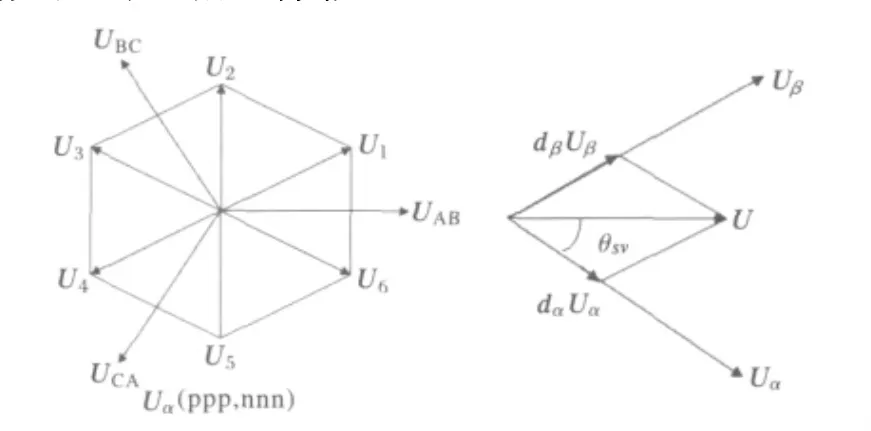
图3 输出线电压空间矢量调制Fig.3 Space vector modulation of the output line voltage
任意时刻输出线电压空间矢量可以由两个相邻的非零开关矢量Uα、Uβ和一个零开关矢量Uo合成得到。开关矢量的作用时间根据空间矢量调制原理和正弦定理计算得到:
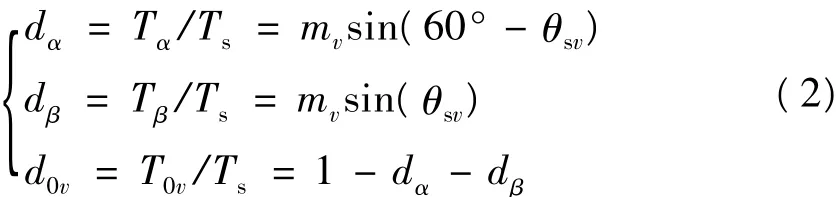
式中:Ts为采样周期;dα、dβ、d0v和Tα、Tβ、T0v分别为Uα、Uβ、U0在一个采样周期中的占空比和作用时间;mv是输出线电压空间矢量的调制系数;θsv是输出线电压空间矢量在当前扇区中的位置。
2.2 虚拟整流器输入相电流空间矢量调制
与输出线电压空间矢量调制类似,根据检测到的输入相电压空间矢量和设定的输入相位差φi,可以确定希望得到的输入相电流空间矢量的位置。任意时刻输入相电流空间矢量Ii可由两相邻的非零开关矢量iμ、iv和一个零开关矢量i0合成得到。同样根据空间矢量调制原理和正弦定理可以得到开关矢量的作用时间:
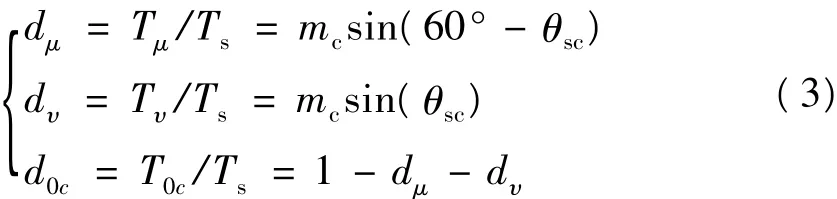
式中:Ts为采样周期;dμ、dv、d0c、和 Tμ、Tυ、T0c分别为iμ、iv、i0在一个采样周期中的占空比和作用时间;mc是输出线电压空间矢量的调制系数;θsc是输入相电流空间矢量在当前扇区中的位置。
2.3 矩阵变换器的空间矢量调制
虚拟逆变和整流器在交-直-交等效结构中是彼此独立进行的,但在实际的矩阵变换器中,中间直流环节是虚拟的,同一开关既要负责输出电压的矢量调制,又要进行输入相电流的矢量调制。因此,将虚拟逆变器输出线电压空间矢量调制过程和虚拟整流器输入相电流空间矢量调制过程结合起来,消去中间直流环节就可以实现对矩阵式变换器的调制,得到控制规律,合成占空比如下:
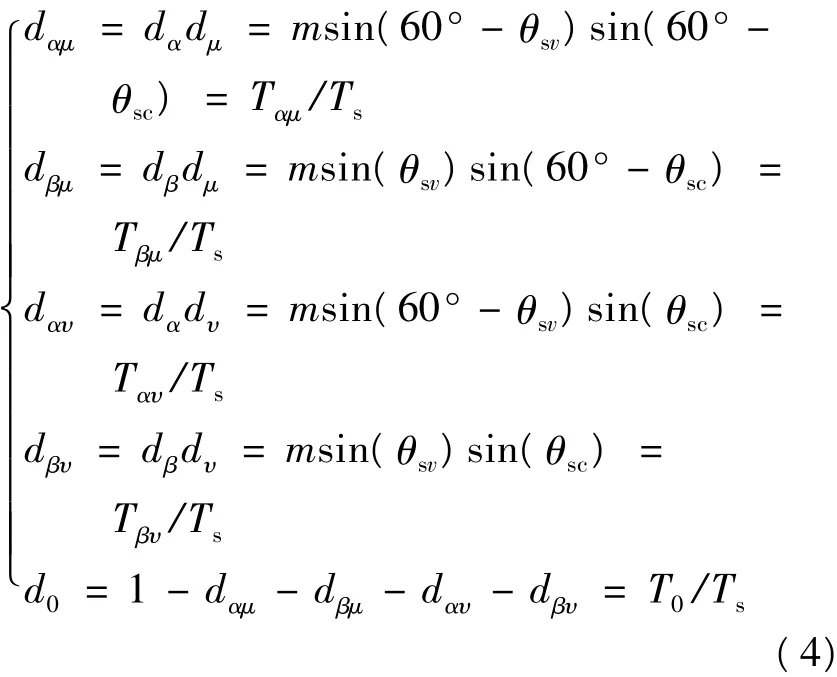
式中:dαμ、dβμ、dαυ、dβν、d0分别是由开关矢量 Uα和iμ、Uβ和iμ、Uα和iυ、Uβ和iυ以及零矢量决定的5 个开关状态。m是矩阵式变换器空间矢量脉宽调制系数,且0≤ m=mvmc≤1。
在矩阵式变换器的每个采样周期内,根据输出线电压所处的扇区和输入相电流所处的扇区,可以确定5个开关状态,利用计算出的占空比控制5个开关状态,从而得到所需的电压。
3 空间矢量调制方法中谐波产生的机理和定量分析
在矩阵式变换器的输入端接以三相正弦电压,通过不同的调制策略,可以在其输出端产生幅值和频率可变的三相电压。但是伴随而来的会出现不同形式的各种谐波。如果把不同调制策略所产生的谐波分为两类:一类是具有共性的谐波,即任何一种调制策略都无法避免的。例如,由于采用PWM而引起的谐波,这些谐波的频率与采样频率的倍数成比例,其中包括在一个采样周期内开关状态的分布所引起的谐波,又如引入零矢量带来的谐波,等等;另一类是和所选调制策略有关的特定谐波,不同的调制策略,会产生不同的谐波。
如果对几种主要的调制策略作一比较,可以得知,用空间旋转矢量来调制矩阵式变换器,物理概念清晰,操作相对简单,避免了烦琐的数学运算,因而得到广泛应用,并取得了突出的效果。但是,采用空间矢量调制后,在矩阵式变换器的输出端,会出现某些特定谐波,它们与这一调制原理密切相关。例如,考虑开关损耗而限制PWM的频率上限,造成空间矢量端点的轨迹由圆蜕变成多边形,引起附加谐波;另外,在任意一个扇区内,被调制方所对应的另一方,电压随时间变化会引起另外一种谐波。在这里,暂且称它为“扇区谐波”,因为这种谐波的次数,与所分的扇面数有关。
为什么会出现“扇区谐波”,以间接空间矢量调制法为例,可以比较直观地说明这一问题。间接空间矢量调制法把矩阵式变换器的功能分为整流和逆变两个部分,整流部分提供“直流电压”,逆变部分输出空间矢量。问题是要保证空间矢量模值不变的条件是,整流部分所提供的"直流电压"必须保持不变。实际上,这个条件是无法满足的。因此,就出现了“扇区谐波”。
本文仅讨论空间矢量调制法带来的扇区谐波。
若定义扇区谐波的含量为

代入空间矢量调制中的实际数值,得到:
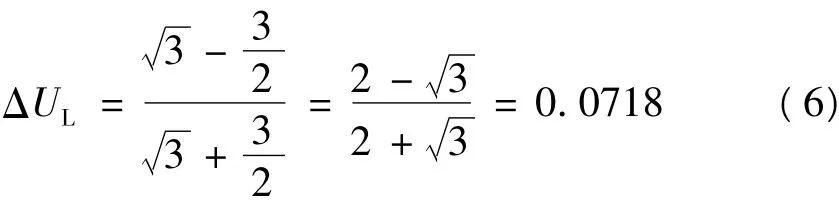
式中:ΔUL为扇区谐波含量;ULmax、ULmin为每个扇区输出线电压的最大值、最小值。
如果输入电压是三相对称正弦系统,并把线电压矢量的端点向外移动ΔUL,即移到平均值的位置,那么在矩阵式变换器的输出端,包括扇区谐波基波分量的线电压空间矢量可以表示为
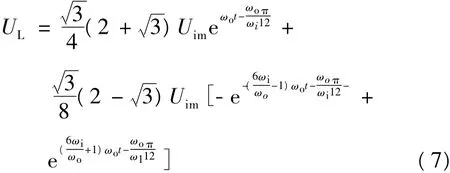
用相同方法,可导出输入相电流表示式:

式中:UL为输出线电压空间矢量;Uim为输入相电压幅值;Iam为输入相电流幅值;IAm为输出相电流幅值;ωi为输入电压频率;ωo为输出电压频率;φi为输入相电压和电流之间的相位差。
从上面两个表示式可以看出,采用空间矢量调制法,在原理上,会在变换器的输出端(或输入端),出现次数与扇区数和输入、输出空间矢量相对旋转速度有关的扇区谐波,其基波分量的幅值是输入(输出)空间矢量幅值的7.18%(按本文规定的扇区谐波含量定义来衡量)。但是,扇区谐波并不影响空间矢量的旋转速度。因此,它仅使负载的附加损耗加大。从谐波表示式还可以看出,扇区谐波的大小与扇区端点矢量的对称性有关,当两端点的矢量相等时,扇区谐波最小。这正是间接空间矢量调制提供的状态。因此,由间接调制转变为直接调制而使扇面的形状改变或为了使输入方的功率因数为1,都会改变这一状态,使扇区谐波加大。
4 矩阵式变换器空间矢量调制仿真
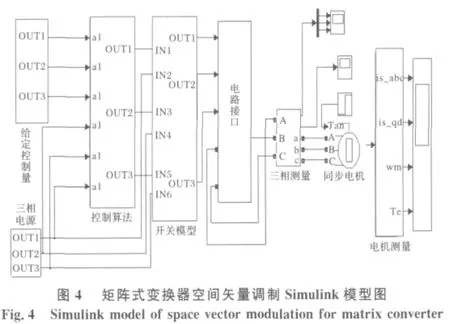
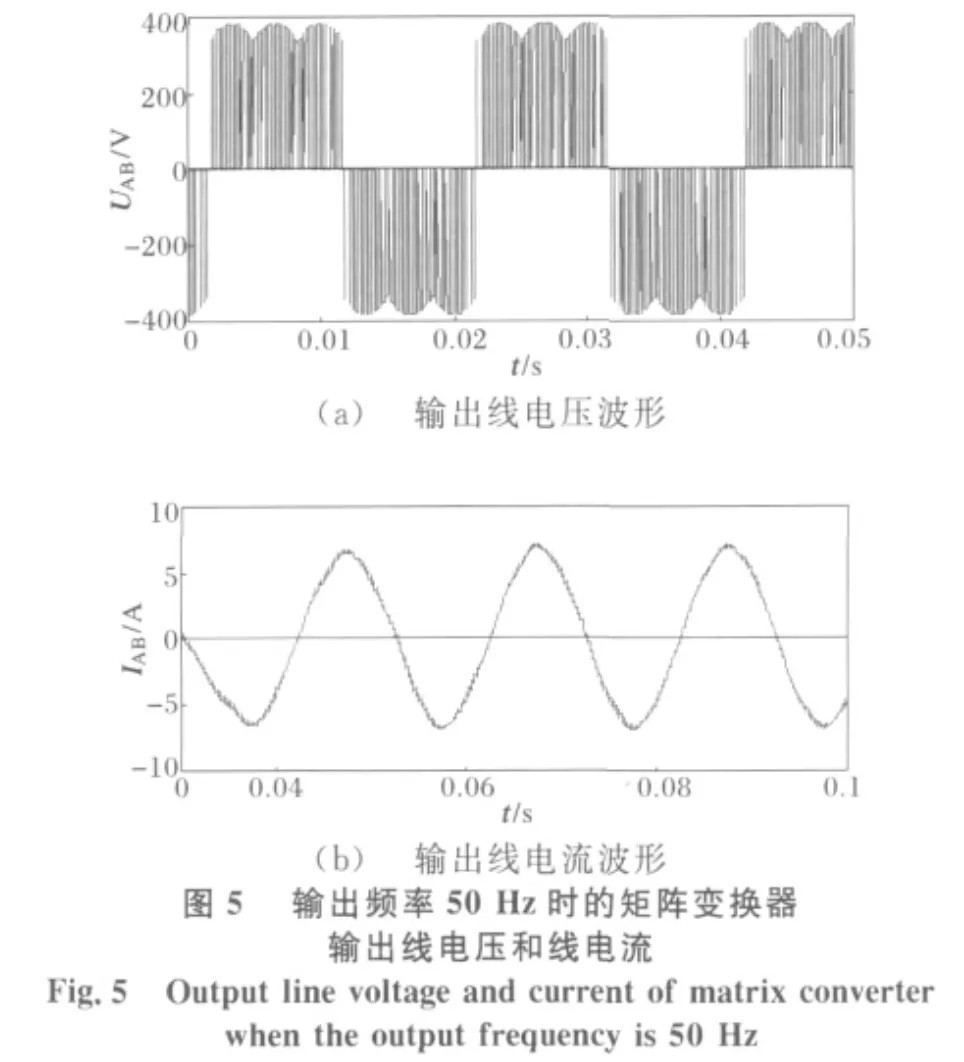
在Matlab中环境中应用Simulink模块,对矩阵变换器空间矢量调制模型进行建模并进行仿真实验[2],建立矩阵变换器的Simulink模型如图4所示。仿真结果如图5和6所示。
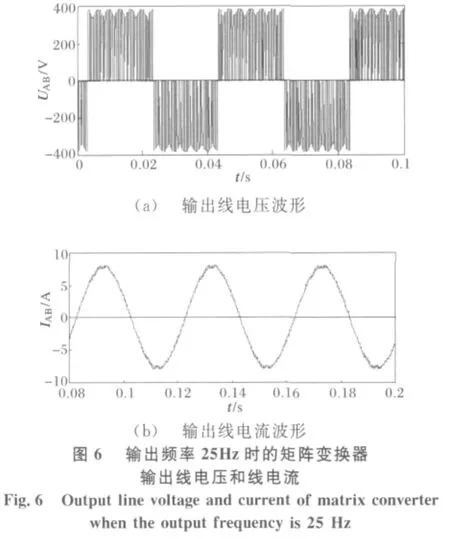
以矩阵式变换器输出频率25 Hz时的输出线电压和输出相电流为例进行谐波分析,得到分析结果如图7、8所示。
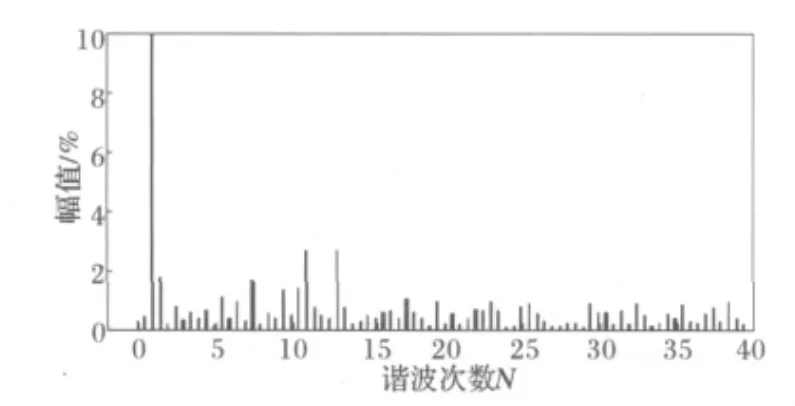
图7 矩阵式变换器空间矢量调制输出线电压波形傅里叶分析Fig.7 Fourier analysis of output line voltage of space vector modulation of matrix converter

图8 矩阵式变换器空间矢量调制输出相电流波形傅里叶分析Fig.8 Fourier analysis of output line current of space vector modulation of matrix converter
当矩阵式变换器输出频率为25Hz时,由仿真波形以及傅里叶谐波分析,可以看出输出端的11、13和23、25次谐波比较明显。这与前面所分析的扇区谐波所得的结论是相符合的。
5 结论
本文以间接空间矢量调制法为例,论述了空间矢量调制策略的基本原理,并提出“扇区谐波”的概念。经过定性、定量分析及仿真后,总结扇区谐波的基本性质如下:
(1)当矩阵式变换器采用了空间矢量调制策略以后,会在其空间矢量上叠加一个与扇区数和输入、输出空间矢量相对速度有关的扇区谐波。按本文所给的定义,扇区谐波基波分量的幅值是输入(输出)空间矢量幅值的7.18%。
(2)扇区谐波仅改变空间矢量的幅值,不影响它的旋转速度,它会使负载的附加损耗加大。
(3)扇区谐波的大小与扇区端点矢量的对称性有关,当两端矢量相等时,扇区谐波最小。因此,以间接空间矢量的扇区为基准,改变扇面的形状或调节功率因数,都有可能改变扇区的状态,使扇区谐波加大。
[1]陈伯时(Chen Boshi).矩阵变流器:技术述评(Matrix converters:Technology review)[J].电力电子(Power E-lectronics),2003,1(1):42 -56.
[2]郭有贵,喻寿益,朱建林(Guo Yougui,Yu Shouyi,Zhu Jianlin).空间矢量调制的矩阵变换器的建模与仿真(The modeling and simulation of space vector modulated matrix converters)[J].系统仿真学报(Journal of System Simulation),2004,16(2):343 -345.
[3]汤宁平,王建宽,吴汉光,等(Tang Ningping,Wang Jiankuan,Wu Hanguang,et al).矩阵变换器的 SPWM控制技术及其实现(SPWM control strategy on matrix converter and its implementation)[J].电工技术学报(Transacitions of China Electrotechnical Society),2003,18(4):25-29.
[4]Huber Laszlo,Borojevic Dusan,Burany nandor.Analysis Design and implementation of the space-vector modulator for forced-commutated cycloconvertors[J].IEE Proceedings B:Electric Power Applications,1992,139(2):103-113.
[5]Rodriguez J.A new control technique for AC-AC converters[C]∥IFAC Control in Power Electronics and Electrical Drives Conference,Lausanne,Switzerland:1983.
[6]王勇,文辉清,吕征宇,等(Wang Yong,Wen Huiqing,Lü Zhengyu,et al).基于MATLAB的矩阵变换器空间相量调制研究(Research on space vector modulation strategy of matrix converter based on MATLAB)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(5):14-19.
