风电场风速的神经网络组合预测模型＊

戴 浪，黄守道，黄科元，叶 盛

(湖南大学电气与信息工程学院，长沙 410082)

随着近年来风力发电规模的不断扩大，风电场并网给电力系统运行带来了一些问题，其中很重要的问题就是对电力系统调度的影响，风速预测对电力系统的功率平衡和经济调度有着非常重要的意义。

风电场风速预测误差不仅与预测方法有关，而且与预测周期以及预测地点的风速特性有关。一般来说，预测周期越短，预测地点的风速变化越缓和，预测误差就越小;反之，预测误差就越大［1］。根据所采用的数学模型不同可分为持续预测法、自回归滑动平均模型法、卡尔曼滤波法和智能方法等。根据预测时间尺度分类，可分为超短期预测和短期预测以及中长期预测。所谓超短期预测一般认为是不超过30 min的预测;短期预测认为是30 min～72 h的预测;中长期预测还存在很大困难，难以得到较好的预测效果。

单一模型对风速预测精度提高有限，使得组合预测受到越来越多的关注。组合预测将各种预测方法的效果进行综合，比单个预测模型更全面，且Bates和Granger证明2种或2种以上无偏的单项预测可以组合出优于每个单项的预测结果能有效地提高预测精度［2］。组合预测模型分为固定权系数与变权系数两种。固定权系数组合预测已经取得了明显的研究成果，但是近年来变权系数组合预测也取得的长足的进步，开始得到广泛应用。

基于神经网络的预测模型在短期风速或风电功率预测广泛应用［3，4］，除此之外，卡尔曼滤波法［5］、向量自回归法［6］也被应用于风速预测，证明了这些方法在风速预测上的可行性。然而组合预测的优势使其在预测上的应用范围越来越广，尤其是基于神经网络的组合预测模型在负荷预测上的应用［7］，而风速预测方法主要集中在单一预测模型上，本文提出了基于遗传算法改进神经网络的风速组合预测模型，预测结果表明其预测精度高于传统线性组合模型的预测精度。

1 风速组合预测模型

风速组合预测的基本思想:设在风速预测问题中，设t时刻的风速实际值为yt(t=1，2，…，n)，若已由m种模型得到该时刻风速预测值分别为y1t，y2t，…，ymt，以这些预测值作为组合预测模型的输入，预测出风速值。组合预测模型表达式如下:

求得的φ(y1t，y2t，…，ymt)即为组合预测模型。

考虑到人工神经网络较强的非线性函数映射能力与遗传算法的优化能力，可建立基于遗传算法优化神经网络的变权组合预测模型，用于得到最终预测结果。

2 神经网络组合预测模型

2.1 遗传算法优化神经网络

BP神经网络各层的初始权值和阈值很大程度上影响着BP神经网络的预测性能，因此选取合适的网络初始权值和阈值可以提高神经网络的预测能力。本文运用遗传算法优化 BP神经网络GAOBP(genetic algorithm optimized back propagation neural network)的目的是通过遗传算法得到最优的初始权值和阈值。其基本思想如下:用遗传算法对网络的初始权值和阈值进行编码构成个体、BP神经网络的预测误差作为该个体的适应度值、通过选择、交叉、变异操作找出最优个体，再对网络进行训练得到预测模型，其基本流程如图1所示。

图1 BP网络优化流程Fig.1 Flow chart of BP network optimization

2.2 组合预测模型

本文选用单一预测模型分别为径向基神经网络(RBF)、BP神经网络以及粒子群优化BP神经网络(PSOBP)，它们的预测值作为神经网络的输入，通过遗传算法优化神经网络的初始权值和阈值，以提高人工神经网络的非线性映射能力及预测精度。其实现流程如图2所示。

图2 组合预测流程图Fig.2 Flow chart of combination forecasting

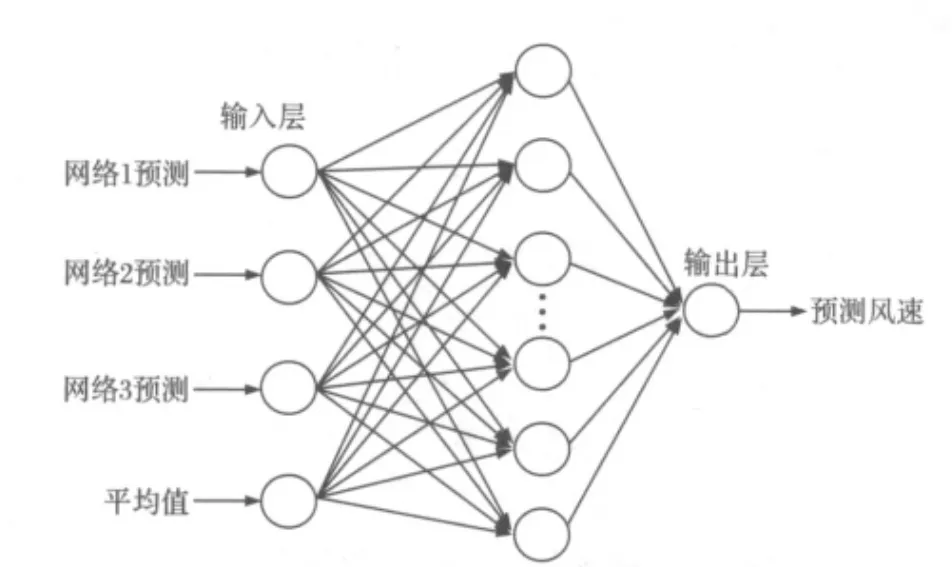
图3 组合预测模型结构Fig.3 Structure of combination forecasting model

3 算例与分析

3.1 数据说明

1996-1998年，中国国家电力公司水电规划总院与美国国家可再生能源实验室联合，对我国东南沿海进行了风能资源评估［10］。其中给出了上海市崇明东旺沙测风塔小时风速测量结果。东旺沙所在的地理位置:东经纬121°56‘，北纬 31°31’，海拔高度8m。测风塔高度为50m，分别在50m、40m和10m高度装设风速计，风速测量起止时间:1998年5月19日-2000年10月20日。

3.2 建立模型

以我国上海崇明东旺沙1998年5月19日-1998年6月19日共31天的小时风速作为样本。小时风速时间序列是每隔一小时采样的实际风速值。该风速时间序列采自50 m高处，前500点风速序列如图4所示。

3.3 预测结果比较

运用BP神经网络模型、RBF神经网络模型、粒子群优化BP神经网络模型以及BP组合模型对上海崇明东旺沙的风速进行预测，预测时间范围取200 h，结果分别见图5、图6，并利用平均绝对误差(MAE)、平方和误差(SSE)以及平均绝对百分比误差(MAPE)三个指标对预测效果进行评价。

图4 采样风速序列Fig.4 Sample wind speed sequence

图5 BP网络与RBF网络预测结果Fig.5 Predictions of BP and RBF network

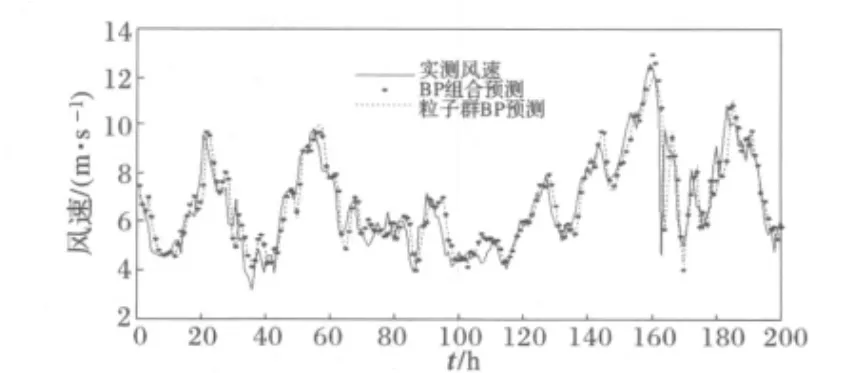
图6 粒子群BP网络与BP组合模型的预测结果Fig.6 Predictions of PSOBP and BP combination forecasting

上述4种模型预测结果平均绝对误差分别为0.6622、0.6582、0.6252、0.6191，平方和误差分别为 170.0393、167.1907、164.3560、161.3130(m/s)2，平均绝对百分比误差分别为0.1029、0.1012、0.0949、0.0929，BP组合模型的预测结果要比前三者都略微精确些，表明组合预测模型预测效果要优于单一预测模型。

传统线性组合模型和遗传算法优化BP网络组合预测模型的预测结果如图7所示。这两种模型预测结果的平均绝对误差分别为0.6184、0.6028，平方和误差分别为 156.4294、148.6387(m/s)2，平均绝对百分比误差分别为 0.0924，0.0907。该结果表明GABP模型预测效果优于传统线性组合预测模型，在三个评价指标上，GABP模型的误差都要小于传统线性组合预测模型。因此，通过遗传算法优化有效提高了BP网络的非线性函数逼近能力，有利于提高风速预测的精度。

图7 线性组合预测与遗传算法优化BP组合预测Fig.7 Linear combination forecasting and GAOBP combination forecasting

除此之外，从上面三个图中可以看出，在风速变化相对平缓的时间段，各种模型的预测能很好地跟随实际风速变化，然而在风速变化剧烈的时刻，无论是单项预测模型还是组合预测模型，其预测值跟随实际风速变化的能力都有所下降，这也是风速预测研究的主要难点之一。

为了更加深入地分析比较单项预测模型与组合预测模型的预测能力，从图中选取一个风速变化剧烈的时间段即图中时间轴上区间［160，179］部分，采用平均绝对误差、平均绝对百分比误差、误差平方和三个评价指标对各预测模型效果进行综合衡量与评价，其结果如表1所示。

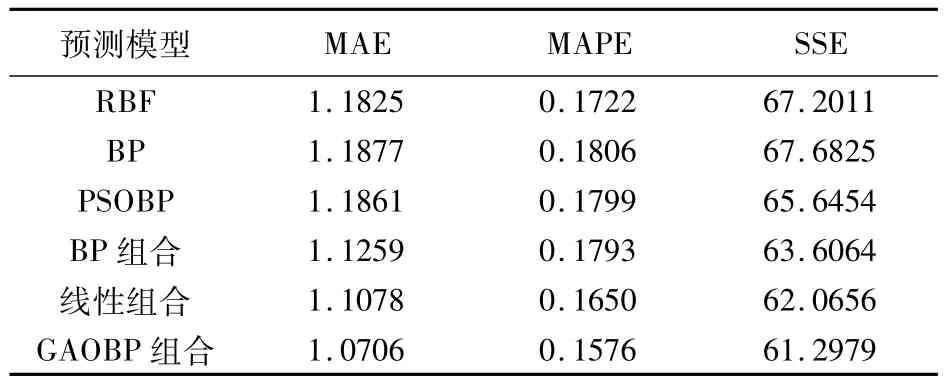
表1 预测误差Tab.1 Forecasting error

从表中可以看，在风速变化剧烈的时间段，任一预测模型的平均绝对误差都有很明显的增加，增幅约0.4m/s。同样，在该时段，各种预测模型的误差平方和也大幅增加。然而，比较各预测模型，发现组合预测模型在该情况下的预测仍然是优于单项预测模型的，而且经优化的组合预测模型较一般组合预测模型仍能维持性能上的优势，表现为更好的预测性能和精度。

4 结语

组合预测模型充分利用了原始数据与各预测模型的预测值，一定程度上实现了数据的平滑滤波处理，弥补单一模型方法的不足，本文提出的组合预测模型的平均绝对误差和误差平方和均低于其中任一单一模型与线性组合预测模型，且文中对基于BP网络和遗传算法优化的BP网络两种组合预测模型也做了比较，不仅证明了组合预测模型在预测精度上的优势，同时也证明了组合预测模型通过适当的优化可进一步提高预测精度。

本文的组合预测模型是一种变权组合预测模型，从实例分析可以得到该组合预测模型在风速预测上的良好适用性，能显著提高风速的预测精度，可作为一种有效的、可行的风速预测模型。

［1］杨秀媛，肖洋，陈树勇(Yang Xiuyuan，Xiao Yang，Chen Shuyong).风电场风速和发电功率预测研究(Wind speed and generated power forecasting in wind farm)［J］.中国电机工程学报(Proceedings of the CSEE)，2005，25(11):1 －5.

［2］Bates J M，Granger C W J.Combination of forecasts［J］.Operational Research Quarterly，1969，20(4):45l－468.

［3］范高锋，王伟胜，刘纯，等(Fan Gaofeng，Wang Weisheng，Liu Chun，et al).基于人工神经网络的风电功率预测(Wind power prediction based on artificial neural network)［J］.中国电机工程学报(Proceedings of the CSEE)，2008，28(34):118 －123.

［4］蔡凯，谭伦农，李春林，等(Cai Kai，Tan Lunnong，Li Chunlin，et al).时间序列与神经网络法相结合的短期风速预测(Short-term wind speed forecasting combing time series and neural network method)［J］.电网技术(Power System Technology)，2008，32(8):82 － 85，90.

［5］潘迪夫，刘辉，李燕飞(Pan Difu，Liu Hui，Li Yanfei).基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型(A wind speed forecasting optimization model for wind farms based on time series analysis and Kalman filter algorithm)［J］.电网技术(Power System Technology)，2008，32(7):82 －86.

［6］孙春顺，王耀南，李欣然(Sun Chunshun，Wang Yaonan，Li Xinran).小时风速的向量自回归模型及应用(A vector autoregression model of hourly wind speed and its application in hourly wind speed forecasting)［J］.中国电机工程学报(Proceedings of the CSEE)，2008，28(14):112 －117.

［7］张亚军，刘志刚，张大波(Zhang Yajun，Liu Zhigang，Zhang Dabo).一种基于多神经网络的组合负荷预测模型(A combination load forecasting model based on multi-neural networks)［J］.电网技术(Power System Technology)，2006，30(21):21 －25.

［8］赵菁，徐克明(Zhao Jing，Xu Keming).神经网络和模糊理论在短期负荷预测中的应用(Application of neural network and fuzzy theory in short－term load forecasting)［J］.电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010，22(3):129 －133.

［9］陆宁，周建中，何耀耀(Lu Ning，Zhou Jianzhong，He Yaoyao).粒子群优化的神经网络模型在短期负荷预测中的应用(Particle swarm optimization-based neural network model for short-term load forecasting)［J］.电力系统保护与控制(Power System Protection and Control)，2010，38(12):65 －68.

［10］Elliott D，Schwartz M，Scott G，et al.Wind energy resource atlas of southeast china［R］.Golden，Colorado，USA:National Renewable Energy Laboratory，2002.