线性系统调节器的设计与内模原理
2011-08-16冯江涛
王 路,冯江涛
(1太原高新技术产业开发区管理局,山西 太原 030006;2山西大学 工程学院,山西 太原 030012)
一个闭环系统必须具有抵抗外部干扰的稳定性,而且还能达到输出调节,即被控量仍然能够跟踪给定值信号,为此需要设计调节器。如果系统状态和外扰状态都可直接测量时,即可作纯增益调节器的设计。否则,设计时应在调节器内部增加内模,才能消除外扰的影响,使此闭环系能达到渐近稳定,而且有满意的动态特性。
1 纯增益调节器的设计[1]
设所研究的装置为
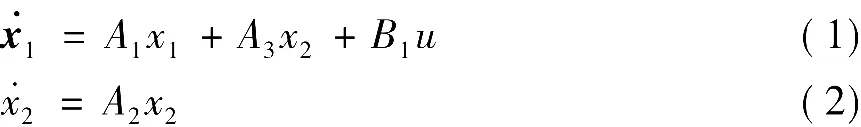

如果存在控制

使闭环系统达到稳定且静态无差,则称式(4)或(F1,F2)为一个纯增益调节器。
在纯增益调节器作用下,闭环系统如图1所示。
当线性受控系统存在外扰x2(t),如果系统状态x1(t)和外扰状态x2(t)均可以直接测量时,也就是外扰状态可直接测量的综合,即称为纯增益调节器,这是一种简单的情况。
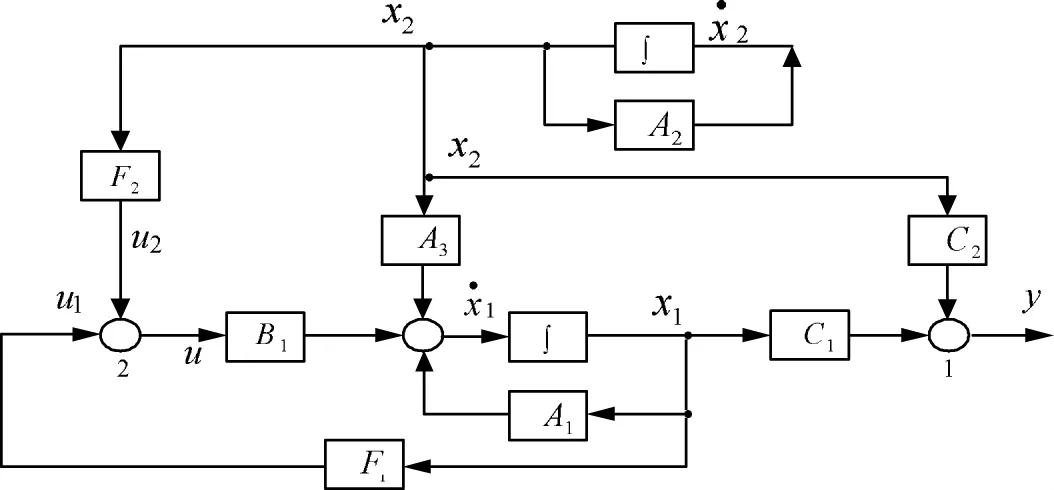
图1 在纯增益调节器作用下的闭环系统方块图
对此,我们使用状态反馈矩阵F1和F2。F1保证闭环系统是渐近稳定的,且使其有满意的动态性能,称F1为镇定矩阵。矩阵F2的作用是使系统输出y(t)不受扰动的影响,称F2为伺服矩阵,要形成外扰状态的补偿通道。
[命题1]系统式(1)、式(2)、和式(3)存在纯增益调节器的充分必要条件为存在矩阵x和u,使得
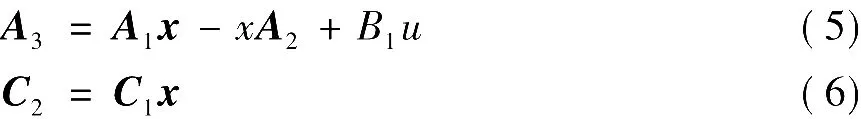
我们在设计纯增益调节器时,应先选择F1,由于(A1,B1)能控(能稳),利用状态反馈极点配置的方法,可选择F1使A1+B1F1有满意的极点。然后,再使用式(5)与式(6),求出x与 u,通过 F2=F1x-u求出F2,达到无静差调节,即得u=F1x1+F2x2,即为纯增益调节器。
2 基于内模原理的调节器设计
当系统状态x1(t)和外扰状态不可直接测量时,用直接状态反馈控制规律u=F1x1+F2x2设计系统是不可能的,应该考虑重构状态反馈的控制规律。当受控系统的A和C完全能观测时,可构造状态观测器,重构系统状态。
设系统式(1)、式(2)和式(3)的一个控制器为

为了简便起见,今后将此控制器简单记为(Vxc:Ac,Bc,Fc,F)。式中,xc为 nc维控制器状态向量;Ac,Bc,Fc,F 分别为具有相应阶数的矩阵。在此控制器的作用下,闭环系统满足:①闭环系统稳定;②达到静态无差,即对任意初值x1(0)、x2(0)和 xc(0),有
在调节器作用下,闭环系统如图2所示。
[命题 2][3]若控制器(Vxc:Ac,Bc,Fc,F)使闭环系统稳定,则它使系统达到输出调节的充分必要条件为存在矩阵x和u,使
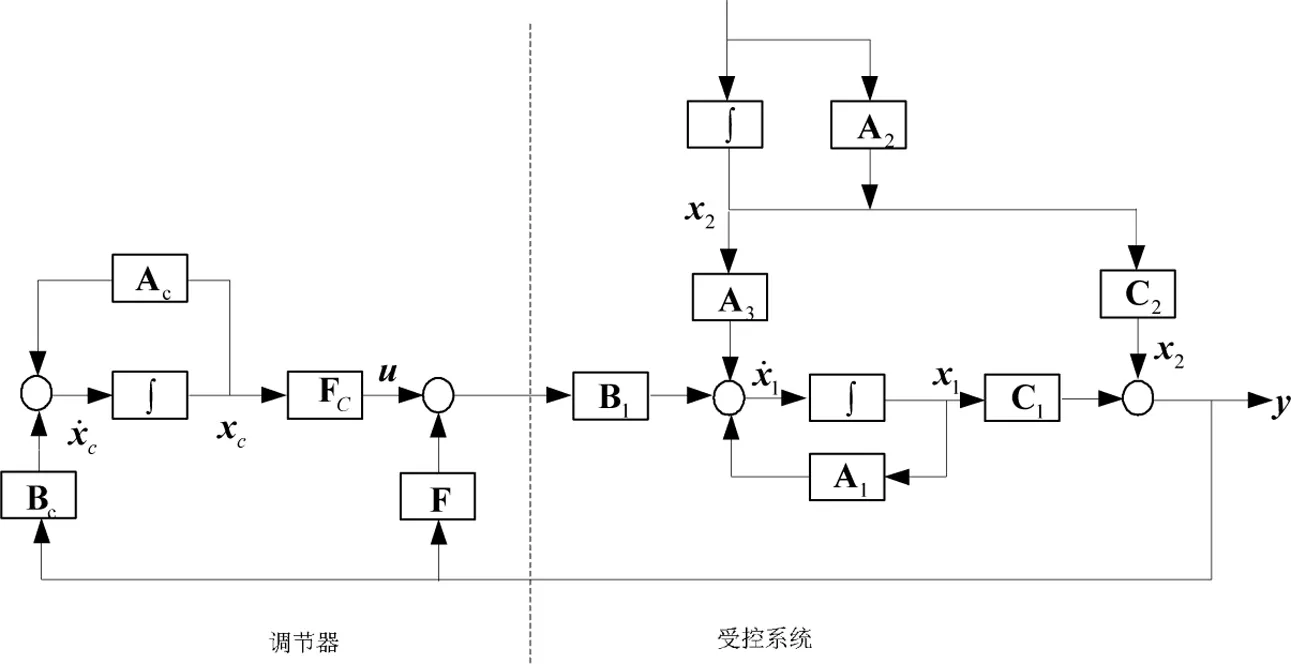
图2 在调节器作用下的闭环系统方块图
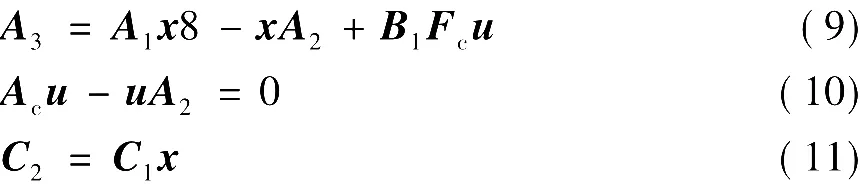
2.1 调节器的设计
调节器的设计主要分二步:①设计一个纯增益调节器;②对增广系统构造观测器,利用观测器对x=[x1x2]T的估计值取代纯增益调节器中x的反馈,则求得调节器。构造调节器的设计思想与设计输出动态反馈补偿器相似。
这个增广系统表述为

式中:
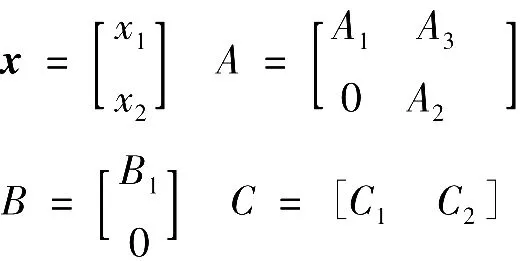
这个增广系统的状态空间为Vx=Vx1Vx2
根据假定(C1,A1)是能观的(能检测的)。如果(C,A)不完全能观(不能检测),容易看出,不能观部分属于Vx2,即在 Vx2中存在一个子空间 Vx22,使Vx2=Vx21Vx22,Vx22为不能观部分等。那么,Vx22中的所有状态对于输出丝毫没有影响,也就是对输出调节没有任何影响。因此,总可假定Vx2=Vx12。
(1)选择F1。使 A1+B1F有满意的极点(稳定)。
(2)选择F2。由式(5)和式(6)可解出u和x1,再令

(3)构造纯增益调节器
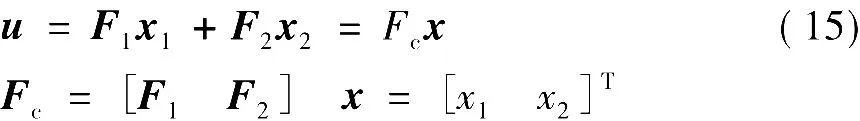
(4)构造增广系统的观测器,由于(C,A)是能观的,可选择Bc,使A+BcC有满意的极点(稳定)。这样可构造增广系统式(12)和式(13)的观测器为
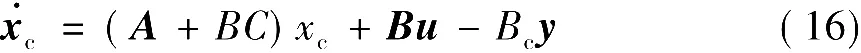
式中,xc= [xc1xc2]T是对x= [x1x2]T的估计值。
(5)构造控制器。用x的估计值xc取代纯增益调节器(15)中的x进行反馈,得
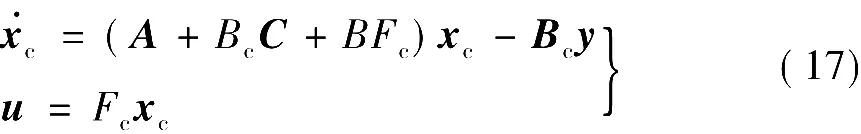
或记为
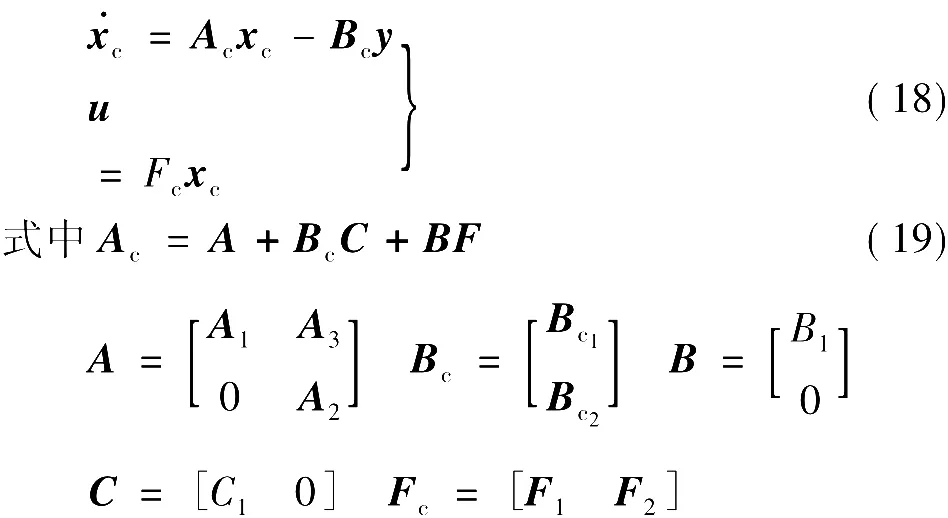
2.2 设计方法
[例]设装置的状态方程为
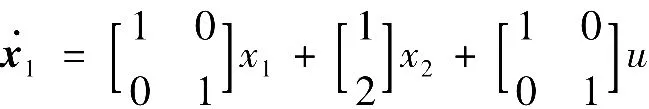
外部输入方程为
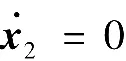
输出方程为
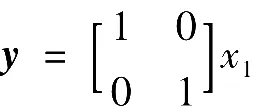
设计一个调节器,并使闭环系统的节点为-2、-2、-1、-1、-2。
解:容易验证系统满足本文的基本假定及有关条件,因而存在调节器。调节器构造的步骤如下:
(2)求F2。矩阵方程式为
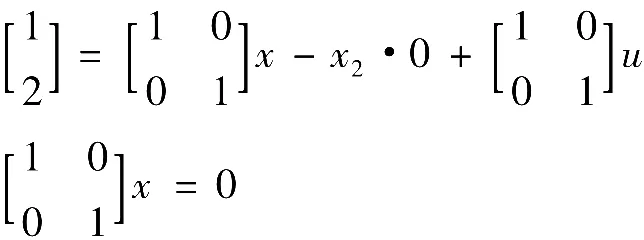
解得
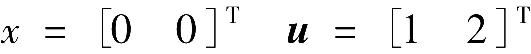
由式(14),则得 F2=F1x- u=-[1 2]T。
(3)纯增益调节器为
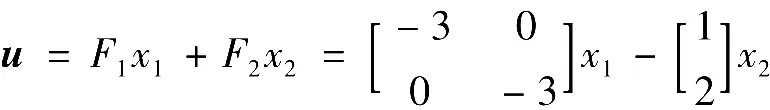
(4)构造增广系统的观测器
由式(15)、式(16)和式(17)可知,增广系统为
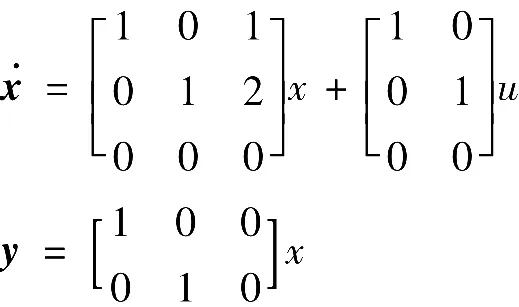
根据构造观测器的方法,可求极点为-1、-1、2的观测器为
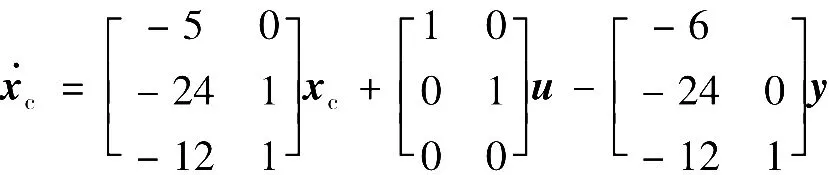
(5)构造调节器,以xc取代纯增益调节器中x=[x1x2]T,得控制规律为
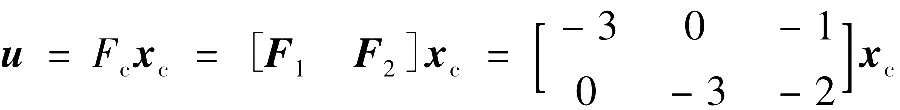
经简单计算得调节器为
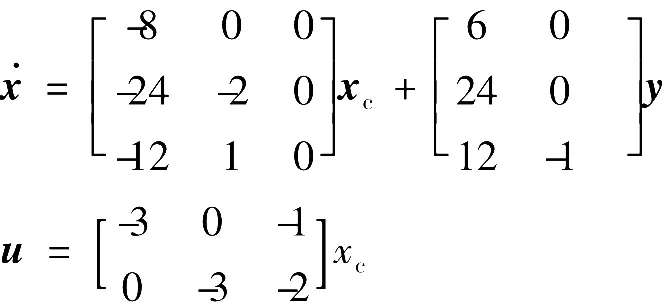
2.3 内模原理
由命题1可知,对于如式(7)和式(8)形式的调节器必有

U可看成映像U:Vx2→Vxc(可以证明U是一一映射),则上式等价于图3。
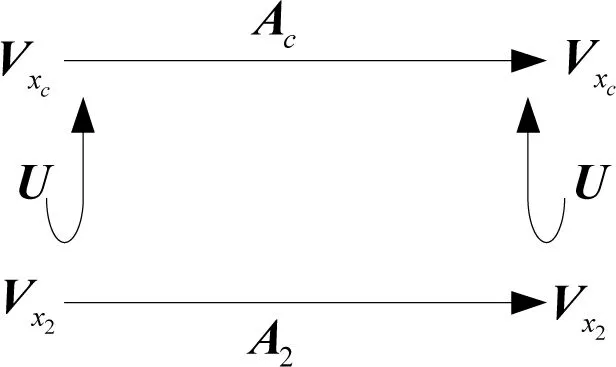
图3 映像交换图
我们知道Ac决定了调节器的动态特性,它是调节器的主体部分;A2代表着外部输入模型。图3是可交换的,即式(20)成立,这意味着外部输入模型通过映像嵌入到调节器,即调节器包含外部输入模型,这就是调节器的内模原理。事实上,正是因为调节器内包含外部输入模型,它才有可能使闭环系统得到输出调节,消除外部输入对系统的影响。
为了进一步说清这个问题,研究调节器的状态方程包含外部输入模型为=0。为了能更清楚地看到调节器中包含外部输入模型,在调节器的状态空间中进行如下坐标变换:
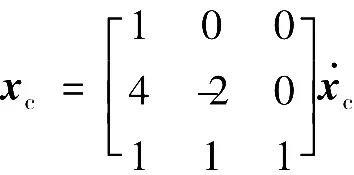
坐标变换后,调节器化为
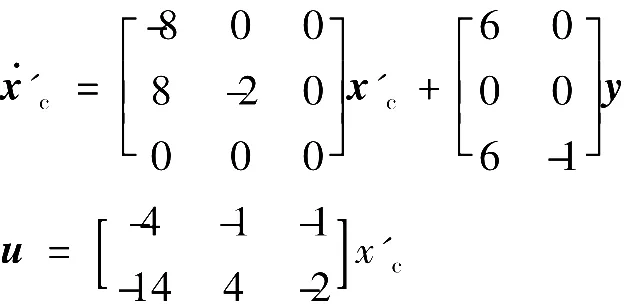
利用式(9)和式(10)可解得u=[0 0 1]T。
因此,U:Vx2→Vxc的像子空间为
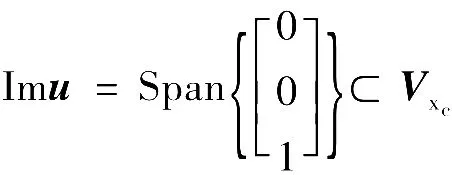
故
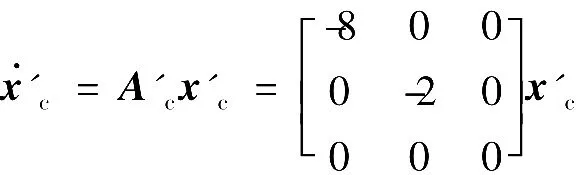
其中x'c3=0即为外部输入在调节器中内模,图4清楚地反映了这一点。
内模原理就是在闭环系统渐近稳定的条件下,系统可实现渐近跟踪和扰动抑制,基本原理在于内模产生的补偿作用,这就要求系统包含一个一阶和二阶积分环节,等价把它们看成是嵌入系统的阶跃函数型和斜坡函数型参考输入模型即内模。
内模原理的特点,与经典控制理论中的一阶、二阶无静差控制相比,内模原理所揭示的是无静差跟踪控制(输出调节)系统结构组成上的一般规律[2]。
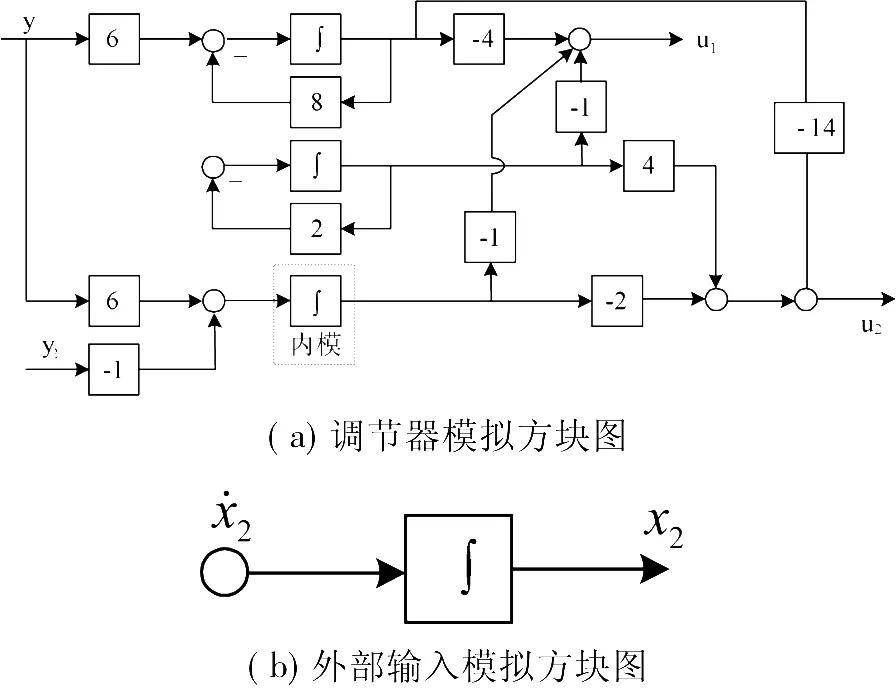
图4 调节器和外部输入模拟方块图
3 结语
本文通过两个命题的引入,结合例题给出了调节器的设计方法和步骤,说明了具有内模原理调节器的鲁棒性,即受控系统和补偿器的参数产生摄动时,即使摄动范围相当大,只要闭环控制系统保持为渐近稳定,则系统必仍具有输出调节(无静差跟踪)的属性,从而在过程控制领域得到广泛的应用
[1] 杨晋萍.在外扰时纯增益调节器的设计[J].太原:电力学报,2010.4
[2] 郑大钟.线性系统理论[M].北京:清华大学出版社,2002年第2版
[3] 涂莑生,董达生.多变量线性控制系统[M].北京:煤炭工业出版社,1998年
