输油管道土压力分析
2011-08-16周正峰凌建明
周正峰,凌建明,梁 斌
(1.西南交通大学 土木工程学院,四川 成都610031;2.西南交通大学高速铁路线路工程教育部重点实验室,四川成都610031;3.同济大学道路与交通工程教育部重点实验室,上海201804;4.中国航空油料有限责任公司,北京100088)
土压力是埋地输油管道承受的最主要恒荷载,同时,施工荷载或交通荷载对管道的影响,也是通过管周土体的传递并最终以土压力形式作用在管道上,因此,土压力计算是管道受力分析的基础。几十年来,国内外许多学者提出了多种管道土压力计算模型,主要包括以下几大类:①基于极限平衡理论的土柱滑动面模型(如 Marston 模型[1]、曾国熙模型[2]等);②从变形条件出发的弹性地基梁模型(如顾安全模型[3]、折学森模型[4-5]等);③经验土压力集中系数模型[6];④土柱法[7]。这些土压力计算方法主要是针对刚性管道,即假定在土压力作用下管道断面的变形量很小,计算时可以忽略不计,管道受到的水平向土压力采用朗肯主动或被动土压力公式进行计算。
然而,埋设于地基中的输油管道为薄壁钢管,在竖向荷载作用下,变形的薄壁钢管使土体位移产生弹性抗力,这抗力的发生与发展又反过来对管壁的进一步继续变形起约束与抑制作用,与此同时,管周土压力集度发生重分布,并趋向均匀化。薄壁钢管管土之间的相互作用对土压力的分布和大小有显著影响,采用针对刚性管的土压力计算方法不再适用,R.C .Prevost,等[8]强调了考虑管土相互作用对薄壁钢管这类柔性管计算分析的重要性。
笔者应用大型通用有限元软件ABAQUS,建立考虑管土相互作用的输油管道有限元模型。应用该模型,分析管周土压力的分布、大小和管土相对刚度,并与现有理论公式计算结果进行对比,说明管土相互作用对管周土压力和管土相对刚度的影响。
1 管道有限元模型
1.1 结构和材料参数
以管径D为610 mm、壁厚δ为10.3 mm的输油管道为例。管材模量Ep为2.05×105MPa,泊松比μp为0.3,不考虑管道自重;管顶埋深H假定为3D(1.83 m);回填土容重 γ1取18 kN/m3,变形模量E1取8 MPa,泊松比 μ1取 0.35,内摩擦角 φ 为30°,不考虑土体黏聚力。模型采用线性平面应变单元CPE 4模拟管道和土体。
管道地基考虑软基和硬基两种情况,变形模量E0分别取8 MPa和80 MPa,泊松比 μ0均取0.35,由于地基呈自平衡状态,故不计容重。管道地基采用弧形基床,基床包角假定为120°。通过收敛性分析,确定模型尺寸为两侧距管道中心3.5D、地基底部距管道中心4.5D。边界条件为对称面采用对称边界,侧面约束水平位移,底面约束竖向位移。管道分析模型如图1。

图1 管道分析模型Fig.1 Pipe analysis model
1.2 管土相互作用模型
管土相互作用涉及到土体与管道2种不同介质间的接触问题,合理模拟管土之间的接触行为是研究埋地管道力学行为的重要前提。管土之间的接触作用属于复杂的边界非线性问题,涉及管土接触面的相对滑动和张开等接触问题。笔者采用库伦摩擦接触模型来模拟管土接触面上的法向和切向作用[9]。
管道与周围土体之间摩擦系数的取值变异性较大,它与管道表面粗糙度、土壤类型、压实度以及干湿状况等因素有关,管土摩擦系数取 0.25[10],同时,也考虑回填土与原地基土之间的摩擦,摩擦系数取0.577(tgφ)。
2 管周土压力分布
整理计算结果,得到管周土压力分布如图2。

图2 管周土压力分布(单位:kPa)Fig.2 Earth pressure distribution around pipe
从图2中可以看出:
1)对于管道地基强度与回填土相同的情况[图2(a)],径向土压力最大值出现在管底C点(50.273 kPa),径向土压力最小值出现在管侧B点(25.146 kPa);对于管道地基强度远大于回填土的情况[图2(b)],径向土压力最小值出现在回填土区的最低点附近,径向土压力最大值出现在与之相邻的管道地基一侧,这是由于管道地基刚度远远大于回填土,根据刚度分配外荷载的原则,径向土压力在回填土与管道地基交界处发生突变。
2)管周环向剪应力分布如图3,管周最大剪应力大致出现在管肩(45°)和管腰(135°)位置,随着地基强度的增大,管道地基部分的管周剪应力有所减小。

图3 管周剪应力分布(单位:kPa)Fig.3 Shear stress distribution around pipe
3)径向土压力和环向剪应力转化为竖向土压力和水平向土压力之后,在管径宽度或高度范围内大致按抛物线分布,同样在回填土与管道地基交界处因刚度差异而发生突变。Marston等土压力理论假定竖向土压力为沿水平直径宽度均匀分布,水平向土压力以朗肯主动土压力表示,其大小随深度按线性规律递增,呈梯形分布。实际上,由于管壳下半圆(反拱)的边界形状将对填土水平向土压力分布产生影响,水平向土压力将随深度增加而递减,有限元分析结果更符合实际情况。
3 管周土压力大小
以管道地基变形模量E0取8 MPa为例,对比分析有限元法、弹性理论解[11]、Marston土压力理论[1]、曾国熙公式[2]、顾安全公式[3]和土压力系数法[6]计算得到的管道土压力系数,如表1。

表1 土压力系数Tab.1 Earth pressure coefficient
表中,竖向土压力系数Ky为管道水平直径宽度范围内受到的平均(括弧内为最大)竖向压力与地面至管顶土柱重量之比,水平向土压力系数Kx为管道竖向直径高度范围内受到的平均水平压力与地面至管道中心回填土重量之比。从表1中可以看出:
1)有限元法和弹性理论法得到竖向土压力系数要小于Marston等理论公式的计算结果,而得到水平向土压力系数要大于Marston等理论公式的计算结果。这主要是由于有限元法和弹性理论法能够考虑管土之间的相互作用。由于管环发生横向侧移和土体对管环侧移的约束,使得管周土压力发生重分布,竖向土压力减小,水平向土压力增大。而Marston等理论公式将管道视为刚性管,忽略了管环的横向侧移。另外,Marston计算水平向土压力采用朗肯主动土压力,而实际上管环变形的趋势总是挤压管侧土体,而不是与土体相脱离,管环侧移方向与水平土压力对管壁的作用方向总是相反,与朗肯主动土压力导出的概念正好相反。因此,有限元法得到的土压力分布形式和大小更符合实际情况。
2)管道受到的竖向土压力总是大于水平向土压力。比较水平向土压力系数与竖向土压力系数的比值可知,有限元法和弹性理论法得到的管周土压力分布较Marston等理论公式计算结果更加均匀,较大的水平向土压力将使在竖向荷载作用下已趋扁平的管环,部分地向正圆恢复,有利于降低管道结构应力和提高管道稳定性。Marston等理论公式低估了管道水平向土压力,使得管道的不均匀受力状态更加严重,再加上对管道竖向土压力的计算偏大,将导致管道的水平径向变形和截面内力计算结果偏大。
4 管土相对刚度
管土相对刚度指管道的自身刚度与管道周围土体的刚度之比,不同刚度的管道在土压力作用下的受力与变形机理不同。管土相对刚度根据管道截面刚度与管周土体刚度的比值来确定,并以管土相对刚度比λ来表示其大小[12]:

在现行理论计算方法中:
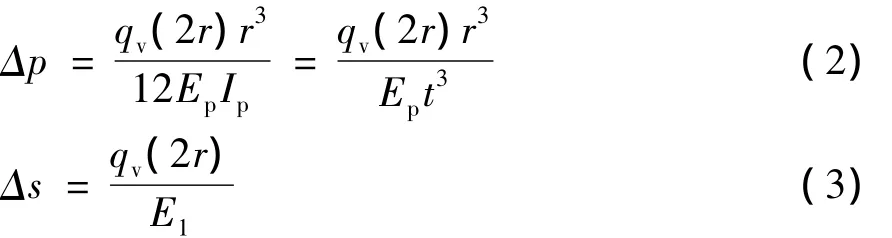
则:

式中:qv为均布竖向压力;r为管道的平均半径;t为管道的平均壁厚;Ep为管道的弹性模量;Ip为管道截面惯性距;E1为回填土的变形模量。
对于管径D=610 mm、壁厚δ=10.3 mm的输油管道,当回填土变形模量取8 MPa时,根据式(4)计算得到的管土相对刚度比λ=0.13,即管道属于柔性管,管道受到的竖向土压力应小于管顶土柱重力[12],而有限元计算结果却表明管顶竖向土压力系数略大于1,即管道与土体的刚度相当。
分析管土相对刚度计算结果的差异:公式(4)在计算管道竖向变形时,采用的计算模型如图4(a)所示。该模型将管道与管周土体完全隔离,仅仅考虑管顶均布竖向压力的作用,忽略了管周土体弹性抗力的影响,并假设管底竖向反力沿管径宽度范围内均匀分布。而实际管道受力状态大致如图4(b)所示,管土之间的相互作用将使管道受力和变形产生重分布。因此,人为地将管道与管周土体完全分开,忽略管道与管侧土体的相互作用,使得管道竖向变形计算结果比实际要大,导致管土相对刚度判定产生偏差。

图4 计算管土相对刚度时的管周土压力分布Fig.4 Earth pressure distribution around pipe as pipe-soil relative stiffness determination
5 结论
1)应用ABAQUS通用有限元软件,采用库伦摩擦模型模拟管土接触面上的法向和切向行为,建立了管土结构有限元分析模型。
2)揭示了管周土压力的分布形态:径向土压力最大值出现在管底、最小值出现在管侧,但当管座地基与回填土刚度不同时,在交界面处发生突变;切向土压力最大值出现在管肩和管腰,最小值出现在管顶和管底。转化成竖向和水平向土压力,在管径宽度和高度范围内大致呈抛物线分布。
3)考虑管土相互作用得到的竖向土压力系数要小于Marston等理论公式的计算结果,得到的水平向土压力系数要大于Marston等理论公式的计算结果,而得到的管土相对刚度要远大于现有理论公式的计算结果,在输油管道力学分析时必须考虑管土之间的相互作用。
[1]Spangler M G.Underground Conduits:An Appraisal of Modern Research[C].Washington,D.C.:Proceedings American Association of Civil Engineening,1948.
[2]曾国熙.土坝下涵管竖向土压力的计算[J].浙江大学学报,1960:5(1):79-97.ZENG Guo-xi.Calculation of vertical earth pressure on the conduit under Culvert[J].Journal of Zhejiang University,1960:5(1):79-97.
[3]顾安全.上埋式管道及洞室垂直土压力的研究[J].岩土工程学报,1981,3(1):3-15.GU An-quan.Investigation of the vertical earth pressure on projecting conduit and underground chamber under a high embankment[J].Chinese Journal of Geotechnical Engineering,1981,3(1):3-15.
[4]折学森,顾安全.高填土下管道土压力的分析[J].西安公路学院学报,1992,12(4):27-33.ZHE Xue-sen,GU An-quan.Study of the earth pressure on conduit under the deeper earth[J].Journal of Xi’an University of Highway,1992,12(4):27-33.
[5]折学森.路基涵洞的土压力计算[J].中国公路学报,1992,5(3):32-39.ZHE Xue-sen.The calculation of vertical earth pressure on buried conduit under roadbed[J].China Journal of Highway and Transport,1992,5(3):32-39.
[6]GB 50332—2002给水排水工程管道结构设计规范[S].北京:中华人民共和国建设部,2002.
[7]GB 50253—2003输油管道工程设计规范[S].北京:中国计划出版社,2003.
[8]Prevost R C,Kienow K K.Basic of flexible pipe structural design[J].Jourmal of Transportation Engineering,1994,120(40):652-671.
[9]庄茁,张帆,岑松,等.ABAQUS非线性有限元分析实例[M].北京:科学出版社,2005.
[10]CECS 141—2002给水排水工程埋地钢管管道结构设计规程[S].北京:中国工程建设标准化协会,2002.
[11]王直民.交通荷载作用下埋地管道的力学性状研究[D].杭州:浙江大学,2006.
[12]黄清猷.地下管计算[M].武汉:湖北科学技术出版社,1987.
