可靠性分析在边坡灰色聚类问题中的应用

杨 枭，李 朋，肖盛燮

(1.重庆交通大学防灾减灾工程研究所，重庆400074;2.西南交通大学土木工程学院，四川成都610031)

滑坡灾害是自然环境的一部分，是仅次于地震和洪水的一种严重自然灾害，它对世界各国造成的经济损失每年可达数十亿美元，并且防灾减灾费用惊人。此外，工程不能及时发挥应有的作用或使用中断，其间接损失更大［1］。由于我国70%的地域为山区，故滑坡发生的频率高，灾害面积广，造成了严重的社会影响，所以研究评价滑坡的新方法具有重要意义。

从20世纪90年代开始，各国相继展开了对滑坡灾害评价的不确定性、模糊性的研究，取得了一系列的研究成果，但大都是分散的、缺乏系统性的。肖盛燮，等［2］在文献中将模糊数学与链式理论结合在一起对边坡的稳定性进行了评估，得到了较为满意的结果，但仍未考虑边坡的可靠性。边坡是一种非线性的开放系统，传统灰色聚类的分析方法基本上考虑了影响边坡稳定性的各类复杂因素，并且计算过程简便，效果较好，它主要是运用各因子的权重值来考虑对边坡稳定性的影响，但这和实际情况的出入比较大，缺乏精度，并且边坡的稳定性也不可能是由唯一的安全系数所确定的，“绝对安全”和“绝对破坏”的边坡是不存在的，如果不考虑可靠度的话，那么得出的边坡分析结果在很大程度上具有迷惑性，同时也可能在工程治理上加大投入，增加成本，所以将可靠性分析运用在边坡的聚类问题当中，分析概率在灰色聚类问题中的处理方法就显得尤为重要。

1 计算模型与分析方案

1.1 可靠性——灰色聚类模型的建立

传统方法中，岩体边坡稳定性灰色聚类法以影响因子为基本变量进行分析。根据各影响因子对边坡稳定性的影响程度不同，给各因子赋以不同的权，从而得到聚类白化矩阵，确定灰类白化函数，最后以此为基础在边坡预测单元和聚类向量之间构造BP神经网络，经过神经网络的学习产生一映射，通过训练好的神经网络对岩体的稳定性进行预测［3］。这种方法虽然能较好的反映出边坡的模糊性、不确定性，以及影响因素的复杂性，但是对于边坡的影响因子只是给出了一个权重值，并没有考虑其作用于边坡上引起滑坡的可能性即概率大小，因此所得结果的经济型较差。

笔者在传统BP方法的基础上，选取“过程降雨量”与“最大地震震级”2因素的因子作为可靠性分析的目标内容，将影响边坡稳定性的其它各因素的因子用权重值表示，其后的分析原理［4］不变，最后将分析的结果与传统方法做一定的比较，过程如下。

1.1.1 滑坡样本因子的调查

根据边坡的空间分布，将其划分成不同边坡单元，对典型边坡的样本因子进行调查，根据对研究对象所在区域已发生滑坡及其他类似滑坡的影响因素分析，分别找出一些影响因子［5］。假设所调查的典型边坡有n个，则分析域S为:

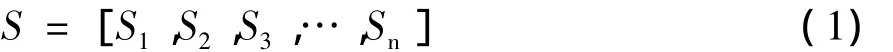
式中:Sj(j=1，2，3，…，n)顺次代表第 j个典型边坡。对每一个典型边坡Sj，有其特征参数(影响因子m个)集X为:

式中:Xij(i=1，2，3，…，m;j=1，2，3，…，n)顺次代表第j个典型边坡的第i个影响因子的特征参数。则典型边坡因子矩阵L(m×n)为:

1.1.2 归一化处理

采用极差法对各影响因子进行归一化处理。

对于优性因子，即可以定量准确描述的因子:

对于劣性因子，即通常属于模糊或者定性描述的因子:

式中:X'ij为极差交换后的数据;Xij为原始数据;Ximax为第i行数据的最大值;Ximin为第 i行数据的最小值。

归一化后的矩阵为:

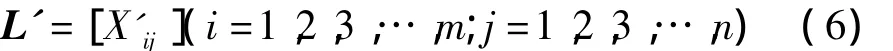
1.1.3 优势分析

分别找出特征参量矩阵中各列数据的最大值，由此构成基准序列X0为［6］:

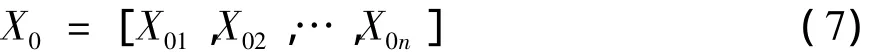
根据以下公式得各典型边坡特征参量序列与基准序列X0之间的关联度集R:

式中:ri为第i种因子与边坡稳定性影响基准序列的关联度;ξi(j)为第j个典型边坡的各种特征参量与基准序列X0中相应的值X0j的关联系数:

式中:ρ为常数，0.1≤ρ≤1。

根据关联度的大小排序构成优劣序，它可以集中反映各因子对边坡稳定性影响程度大小。在边坡预测时，取优势因子(主因子)作为基本变量。根据优势分析所得的优劣序，对那些相对于稳定性关联度大的因子赋予较大的权，反之则赋予较小的权。将各因子与特征序列的关联度大小的比重作为其权系数εi:

1.1.4 因子的概率化

在规定的时间内，边坡执行功能时，各个因子作用在边坡上并不一定会引起滑坡，这就需要对该区域的滑坡历史进行分析，进而将可靠度引用进来，根据边坡所在的研究区域，通过统计方法得到各个因子特征参数的样本及其分布规律。

根据文献［7］，设有一因子时间序列观测值Xt={xt1，xt2，…，xtn}，分别取观测值的最小值 Xtmin和最大值Xtmax作为该因素时间序列区间的下限和上限，并将其划分为r个子区间，每个区间的宽度为Δxti，则:

定义影响边坡因素观测值序列在第i个子区间的分布概率为:

则可靠度为:

式中:nti为研究时段内观测值位于第i个子区间时滑坡发生的个数;Nti为研究时段内滑坡发生的总样本数;M为子区间个数。

1.1.5 可靠度的引入与聚类白化矩阵的确定

将可靠度H与归一化处理后的可靠度分析目标因子参数相乘，将其他的各个因子赋以各自的权重，这样就得到了聚类白化矩阵D，此矩阵就是进行稳定性边坡预测的变量矩阵，并且考虑了概率在边坡分析中的影响。

1.1.6 确定白化函数及BP神经网络结构

若有1，2，…，m 个聚类指标，1，2，…，p 个稳定性类别，令 fki(x)(k=1，2，…，p;i=1，2，…，m)为灰数k⊗i的白化函数，进而得到聚类权矩阵η =［ηki］、空间预测单元矩阵 f=［fki(dij)］、聚类向量σ=f×η，最后利用传统方法中的BP神经网络对岩体稳定性进行训练［8］，如图(1)，从而得到最终结果。

1.1.7 因子的选取及等级的划分

根据相关人员在三峡库区的工程实践［9］，选定9个与边坡稳定性相关联的因素，等级划分见表1。

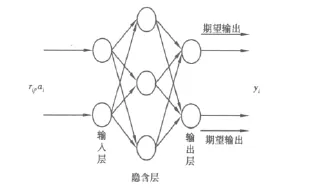
图1 BP神经网络结构Fig.1 Structure of BP neural network

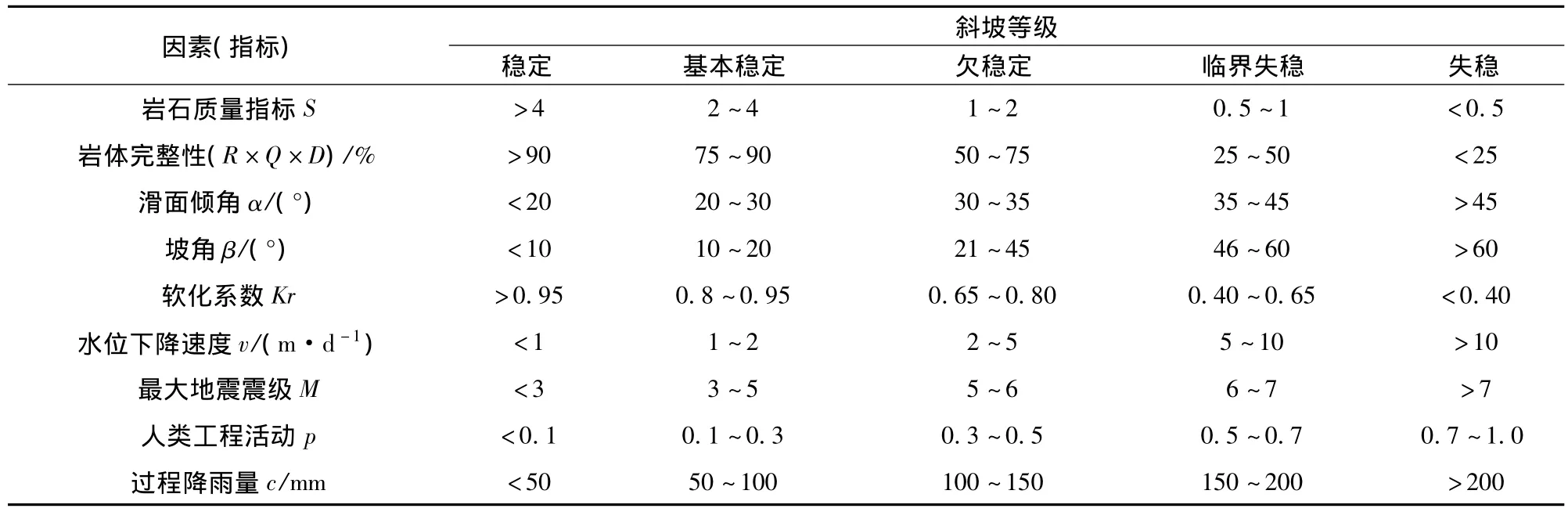
表1 边坡等级划分Tab.1 Grading of slope

1.2 工程算例

对重庆万州江南新区陈家坝晒网村5个可研型较高的典型边坡进行了数据分析，根据张永兴，等［10］在文献中对定量、定性(模糊)因子的划分，笔者在表1中的9个影响因子当中选取岩体完整性、滑面倾角、坡角、软化系数为优性因子，选择岩石质量指标、水位下降速度、人类工程活动为劣性因子，选取过程降雨量以及最大地震震级为概率及可靠性分析的目标内容，假设边坡所在地区在预计时间内可能的最大过程降雨量为55 mm，最大地震震级为4.7，通过对国土局提供的该周边地区近10年来降雨与地震引发的滑坡个数进行统计，将其关系列入图2。

通过取样调查，5个边坡的影响因子指标见表2，表中的行、列，对应于矩阵L的行、列。

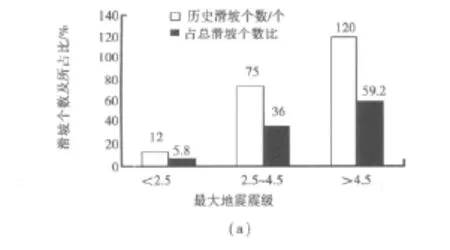
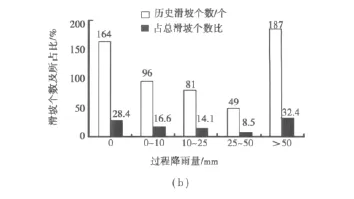
图2 过程降雨量及地震震级与历史滑坡个数的关系Fig.2 Relationship between history landslide number with processrainfall and magnitude

表2 各边坡的影响因子指标Tab.2 Impact factor indicators of every slope

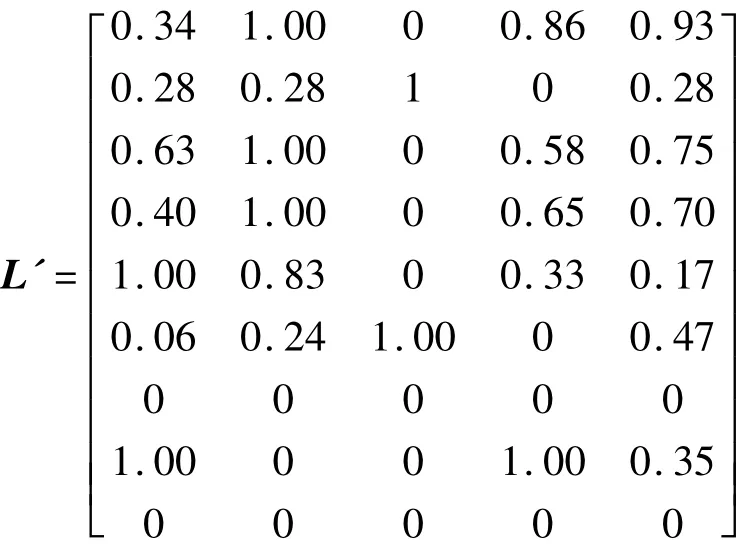
由表2，通过公式(4)、公式(5)可得归一化后的因子矩阵L'。

根据公式(7)，得到基准序列X0:

最后，由公式(8)～公式(10)得到优劣因子权重系数，见表3。

表3 优劣因子的权重系数Tab.3 Weight coefficients of factors

由L'和表2、表3可得聚类白化矩阵D。

由图(2)可知，最大过程降雨量的pti为32.4%，最大地震震级的pti为59.2%，由公式(13)可知，两者的可靠度 H 分别为67.6%，40.8%，这里将1、2、3边坡单元作为学习样本R，把4、5边坡单元作为测试样本。根据前述的方法，同时将“过程降雨量”与“最大地震震级”的可靠度与矩阵D所对应的影响因子相乘，按图1构造人工神经网络，网络选择27个输入节点，一个隐含层64个节点和5个输出节点，即 ANN(27，64，5)，取学习率初值，惯性系数及误差分别为 0.2，0.85，0.001，对该网络进行训练，训练结束误差为0.000 898。利用训练好的神经网络模型ANN(27，64，5)对边坡单元4、5进行预测，最后将预测结果与传统的BP法分析结果列于表4。

表4 各预测结果与传统BP法结果对比Tab.4 Comparison of predicted results with traditional BP method

1.3 结果分析

从表4可以看出，引入可靠度过后不仅预测结果与传统方法分析结果是一致的，并且由于可靠度与所对应的影响因子相乘后提高了传统BP法的训练次数，从而减少了输出误差，使得结果的精度更高，这说明将可靠度引入到传统方法过后，能较好地处理岩体边坡稳定性与影响因素之间灰色非线性映射关系，对岩体边坡的稳定性能作出比较准确、客观的预测结果，并且在不考虑其它因素的情况下，从图2可以看出作为预测的4、5号边坡在降雨和地震的单独作用下发生滑坡的概率pti分别为32.4%和59.2%，即可靠度H分别为67.6%和40.8%，说明了4、5号边坡在降雨的作用下可靠度较高，而在地震来临时发生滑坡的可能性较大，综合了其它因素过后，4号边坡处于较稳定状态，应列入重点监测对象，5号边坡处于欠稳定状态，应采取相应的工程措施。

2 结论

笔者对晒网村的5个典型边坡进行了稳定性分析，考虑了“过程降雨量”与“最大地震震级”作用在边坡上时的可靠度，分析后所得结果与传统BP法所得结果一致，精度较高，得出了2因素单独作用在边坡时的可靠度，为工程防护与治理提供了参考，为了便于分析，只选择了2个因素的可靠度，还可以将其它因子的可靠度大小一并找出，进行叠加，结果会更接近于实际，在选取概率因子时，仅使用了局部“滑坡个数”来评定可靠度，理论还有待于进一步提高。

［1］谢全敏，夏元友.基于神经网络的岩体边坡稳定性的灰色聚类空间预测法及其应用［J］.灾害学，2001，16(2):1-6.XIE Quan-min，XIA Yuan-you.Spacial forecast method and application of grey clustering of rock slope stability based on neural network［J］.Disaster，2001，16(2):1-6.

［2］肖盛燮.灾变链式理论及应用［M］.北京:科学出版社，2006:1-3.

［3］谢全敏，夏元友.滑坡灾害评价及其治理优化决策新方法［M］.武汉:武汉理工大学出版社，2008:55-60.

［4］夏元友，肖峰.斜坡稳定性评价的动态聚类分析方法［C］//第六届全国岩石力学与工程学术会议论文集.北京:中国科学技术出版社，2000:562-565.

［5］袁勇涛.AHP-FUZZY综合评价在边坡稳定性中的应用［J］.工程技术与产业经济，2010，1(2):23-24.YUAN Yong-tao.The application of AHP-FUZZY comprehensive evaluation on the slope stability［J］.Engineering Technology and Industrial Economy，2010，1(2):23-24.

［6］夏元友，朱瑞赓.岩质边坡稳定性多人多层次模糊综合评价系统研究［J］.工程地质学报，1999，7(1):46-53.XIA Yuan-you，ZHU Rui-geng.Research of multiplayer multilevel fuzzy comprehensive evaluation system about rocky slope stability［J］.Journal of Engineering Geology，1999，7(1):46-53.

［7］史玉峰，宁津生.基于信息熵的滑坡体稳定性分析研究［J］.煤炭学报，2005，30(增刊):51-54.SHI Yu-feng，NING Jin-sheng.Analysis research of landslide stability based on the information entropy［J］.Coal Journal，2005，30(Supp):51-54.

［8］徐玉秀，任立义，钟建军.基于专家系统与神经网络集成的故障诊断的应用研究［J］.振动与冲击，2001，5(20):61-66.XU Yu-xiu，REN Li-yi，ZHONG Jian-jun.Application research of fault diagnosis based on the expert system and neural network ensemble［J］.Vibration and Shock，2001，5(20):61-66.

［9］张淑辉.基于地统计方法的滑坡因子敏感度分析［J］.武警工程学院学报，2010，26(4):4-6.ZhANG Shu-hui.Sensitivity analysis of landslide factors based on the statistical method［J］.Journal of Armed Police Engineering College，2010，26(4):4-6.

［10］张永兴，文海家，欧敏.滑坡灾变智能预测理论及其应用［M］.北京:科学出版社，2005:82-83.