Research on shape optimization of CSG dams
2011-08-16XinCAIYingliWUJiangangYIYuMING
Xin CAI*, Ying-li WU, Jian-gang YI, Yu MING
1. College of Mechanics and Materials, Hohai University, Naijing 210098, P. R. China
2. College of Water Conservancy and Hydropower Engineering, Hohai University, Naijing 210098, P. R. China
3. Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, P. R. China
Research on shape optimization of CSG dams
Xin CAI*1,2, Ying-li WU3, Jian-gang YI2, Yu MING2
1. College of Mechanics and Materials, Hohai University, Naijing 210098, P. R. China
2. College of Water Conservancy and Hydropower Engineering, Hohai University, Naijing 210098, P. R. China
3. Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, P. R. China
The multi-objective optimization method was used for shape optimization of cement sand and gravel (CSG) dams in this study. The economic efficiency, the sensitivities of maximum horizontal displacement and maximum settlement of the dam to water level changes, the overall stability, and the overall strength security were taken into account during the optimization process. Three weight coefficient selection schemes were adopted to conduct shape optimization of a dam, and the case studies lead to the conclusion that both the upstream and downstream dam slope ratios for the optimal cross-section equal 1:0.7, which is consistent with the empirically observed range of 1:0.6 to 1:0.8 for the upstream and downstream dam slope ratios of CSG dams. Therefore, the present study is of certain reference value for designing CSG dams.
CSG dam; shape optimization; sensitivity analysis
1 Introduction
In the late 20th century, the cement sand and gravel (CSG) dam, a new type of dam with the advantages of the concrete face rockfill dam (CFRD) and the concrete gravity dam (CGD), has drawn the attention of more and more experts throughout the world. Generally, CSG dams have small cross-sections compared with other kinds of dams, and can be constructed using small amounts of rockfill within a short period of time. In addition, CSG dams can be constructed on the soft soil foundations and have significant capability of anti-earthquake. The CSG dam was originally suggested by Raphael (1970). Later, Londe and Lino (1992) proposed that both the upstream and downstream dam slope ratios could be 1:0.7, and pointed out that the waterproof panel should be installed on the upstream surface. Besides, a kind of hard fill instead of concrete could be used, thus the requirements for roller-compacted concrete (RCC) performance and technology could be lowered, and the total cost of the dam could be reduced while the level of its security remained high. Due to insufficient knowledge of CSG dams, the design of CSG dams is mostly based on the experience of rolled rockfill dams at present. Research on cross-section optimization of the dam shape can only be found in Cai et al.(2008a) and Shi (2006), which only followed the experiences of CFRDs and poorly reflected the features of CSG dams. Thus, the multi-objective optimization method was adopted for CSG dam shape optimization in this study, in order to improve the economic efficiency as well as the dam’s strength, stiffness, and stability.
2 Basic principles of multi-objective optimization
The multi-objective mathematical model for design variableX={x1,x2,…,xn} can be expressed as (Xie et al. 2002; Dimou 2009)
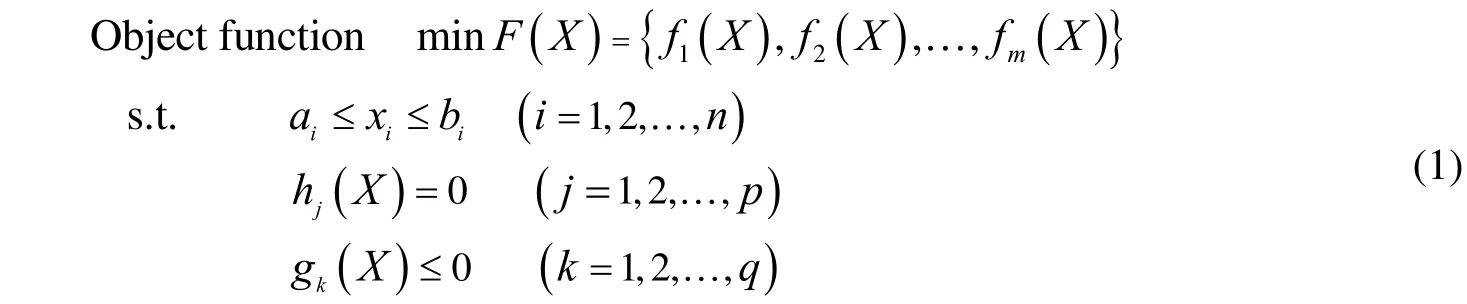
wherexi(i=1,2,…,n)is the design variable;fi(X)(i=1,2,…,m)is the objective function;aiandbiare the upper and lower limits of variablexi, respectively;hj(X)is the non-upper and non-lower limit equality constraint;pis the number of equality constraints;gk(X) is the non-upper and non-lower limit inequality constraint; andqis the number of inequality constraints.
As to the problems in the non-uniform model, in which some of the objective functions tend to become minimum, while the rest become maximum,ttargetsfi(X)(i=1,2,…,t)are set to satisfy the minimum problem, and the remainingm-ttargets,fi(X)(i=t+1,t+2,…,m)are set to satisfy the maximum problem. Then, the non-uniform problem can be described as

The efficacy functions for the objective functions are constructed, and the objective functions are normalized. The efficacy functions can be described as
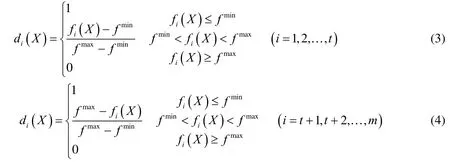
The non-uniform multi-objective problem can be transformed into a uniform minimum problem, which can be described as
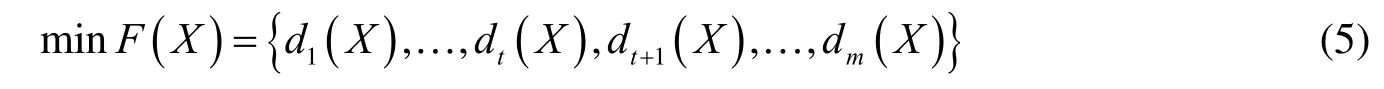
Then, the single objective function can be constructed as follows:
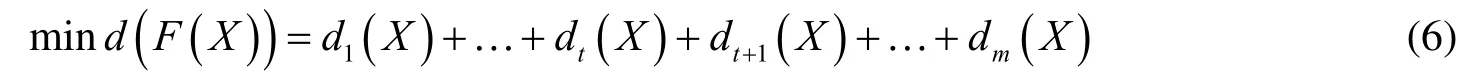
The optimal solution to Eq. (6) can be regarded as the optimal solution of the multi-objective function.
In order todescribe the degree of influence of each objective function, the term of each objective function should be multiplied by a weighting coefficientωi, which satisfies

Substituting the weight coefficient into Eq. (6) gives the following equation:
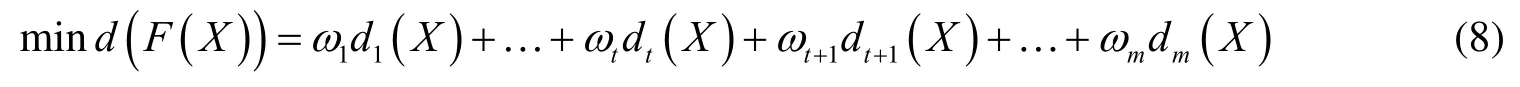
3 Impacts of upstream and downstream dam slopes on displacement and stress of dams
A typical cross-section of the Chengping CFRD was selected as the prototype to establish a numerical analysis model for the study. The dam is built on the bedrock with a height of 74.6 m and a normal water level of 71.6 m (Luo 2002; Cai et al. 2008b). The model was discretized with 4 310 nodes and 4 657 elements, of which 4 020 were elements of the CSG material and 120 were those of the concrete face. The range of the upstream and downstream dam slope ratios of the dam varies from 1:0.4 to 1:1. Contact elements (60 elements) were adopted to simulate the contact surface between the concrete face and the dam body. The vertical and the horizontal constraints were set at the bottom of the dam with water loads exerting on the concrete face to simulate the storage situation. The constitutive equation of the CSG material used for numerical analysis was established based on a series of large scale triaxial tests, compression strength tests, and bending tests. The constitutive equation could describe the real stress-strain relation of the CSG material. Detailed descriptions of the constitutive equation and parameters were obtained from Cai et al. (2010) and Wu (2010).
The upstream and downstream dam slope ratios of the existing CSG dams vary mostly from 1:0.6 to 1:0.8, and the cross-section, with the upstream and downstream faces symmetric to each other, is designed as a symmetrical trapezoid. To study the impacts of the dam slope on the displacement and stress distributions of the dam body, the upstream and downstream dam slope ratios varying from 1:0.4 to 1:1 were taken into account, and the asymmetry of the upstream and downstream dam slopes was considered as well. The upstream and downstream slope ratios were termeduandd, respectively. Considering that the CSG dam was modeled to sit conceptually between CFRDs and CGDs, the variation of the upstream and downstream dam slopes is similar in scope to that of the two dam types. Analysis was conducted on 28 combinations of dam slopes in order to study the impacts of the dam slope on the displacement and stress distributions of the dam and the sensitivities of the maximum horizontaldisplacement and the largest settlement to water level changes.
The train of thought for sensitivity analysis is as follows (Cai 2004): assuming there is a system, the characteristic valuePis mainly determined bynfactorsα={α1,α2,…,αn}, and the system model isIn a reference state,, there exists a corresponding characteristic valueP*in the system. When each factor varies within a certain range, the degree ofPdeviating from the reference characteristic value of the system can be defined asΔP, andΔPPis defined as the sensitivity.
The maximum horizontal displacement, the largest settlement, and the maximum stress level of the dam varying with the dam slope were achieved through analysis of the CSG dam under the conditions of 28 combinations of dam slopes, as shown respectively in Figs. 1, 2, and 3.
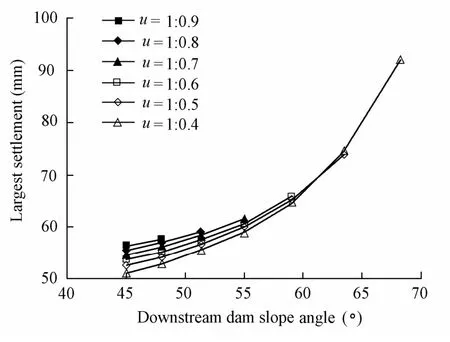
Fig. 2 Relationship between largest settlement of dam and upstream and downstream dam slopes
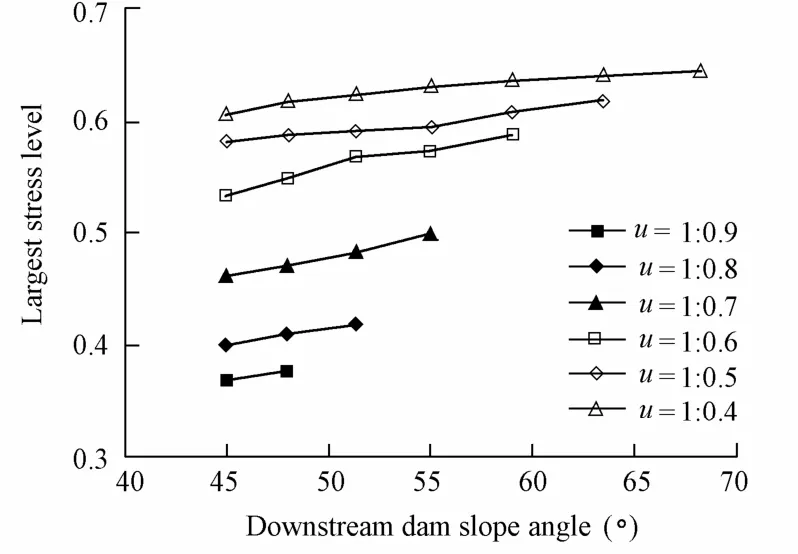
Fig. 3 Relationship between largest stress level and upstream and downstream dam slopes
As shown in Table 1, the sensitivities of the maximum horizontal displacement and the largest settlement of the dam to the water level change increase with the decrease of the dam cross-section. As the cross-section decreases to a certain extent, for instance, the upstream and downstream dam slope ratios are greater than 1:0.6 (51.34° of the dam slope angle), the sensitivities increase rapidly, the change rate of sensitivity is consistent with that of themaximum horizontal displacement (Fig. 1), and the maximum settlement varies with the dam slope as well (Fig.2). The sensitivity of the maximum horizontal displacement of the dam is much higher than that of the largest settlement to the water level change. This indicates that the horizontal displacement of the dam is greatly influenced by the change of water level in the operation period, which should be paid attention to. In addition, the maximum stress level increases with the decrease of the dam cross-section (Fig. 3), adequately reflecting that although the steeper dam slope can generate higher economic efficiency, it will reduce the strength of a dam and thus give rise to security problems. When the upstream dam slope remains unchanged, the change of the downstream dam slope has little effect on the maximum stress level of the dam, which shows that the maximum stress level is mainly influenced by the dam cross-section area and the upstream dam slope.
4 Multi-objective optimization of CSG dam cross-sections
4.1 Two-objective optimization of dam cross-sections
The area of the dam cross-section directly reflects the economic efficiency of the dam, and the construction costs are generally proportional to the dam cross-section area. The sensitivities of the maximum horizontal displacement and the largest settlement of the dam to the water level change can reflect the horizontal stiffness and vertical stiffness of the dam. An initial screening was taken of 28 dam slope combinations to conduct the two-objective optimization of the dam cross-section by considering the economic efficiency and thehorizontal and vertical stiffness.
First, the dimensionless treatment was conducted of the dam cross-section area. The dam upstream and downstream cross-section areas with a dam slope ratio of 1:1 were made the basis cross-sectionS*, the dam cross-section area of different slopes was, and the economic coefficient of the dam body was defined asφS=SaS*. It can be seen that the smaller the value ofφSis, the higher the economic efficiency of the dam is. Taking the sensitivities of the maximum horizontal displacement and the largest settlement to the water level change as the standard to reflect the dam safety performance, it can be seen that the greater the sensitivity is, the lower the safety of the dam is. Ifφwis defined as the sensitivity coefficient, andhwwhereφandswφare the sensitivity coefficients of the maximum horizontal displacement and the largest settlement of the dam to the water level change, respectively, andandare the maximum sensitivity coefficients of the maximum horizontal displacement and the largest settlement of the dam to the water level change, respectively.φwcomprehensively reflects the sensitivities of the horizontal displacement and the settlement of the dam to the water level change. The maximum horizontal displacement of the dam is inversely proportional to its own stiffness under loads, and the law of the sensitivity coefficient to the water level change varying with the dam cross-section also reflects the varying relationship between the stiffness and the cross-section area of the dam.
In the case of a two-objective optimization problem of the economic coefficientφSevaluated with the cross-section areaSaof the CSG dam and the sensitivity coefficient of the dam to the water level changeφw, it is transformed into a single-objective optimization issue using the linear weighting unified-objective method and the mathematical model. The non-inferior solution is obtained by solving:

whereS0is the allowable value of the maximum cross-section area.
By sorting the calculation results of 28 dam slope combinations, the variation of theF(X)function corresponding to different dam slope combinations was obtained, as shown in Fig. 4. The calculated results show that the functionF(X) reaches a minimum value of 0.507 2 when both the upstream and downstream dam slope ratios are 1:0.6, and several cross-section slope ratios with the value ofF(X) close to the minimum value are:u=d= 1:0.7;u =1:0.6, andd =1:0.7;u =1:0.5, andd =1:0.8;u =1:0.5, andd =1:0.7; andu =1:0.5, andd=1:0.6.

Fig. 4F(X) function corresponding to different upstream and downstream dam slopes
4.2 Multiple-objective optimization of dam cross-sections
As cross-sections of the CSG dam have the characteristics of both CFRDs and CGDs, and there is no design specification available for CSG dams; its design was checked according to the design specifications of both CFRDs and CGDs in the study.
Further studies were conducted on the six combinations of the upstream and downstream dam slopes obtained from the initial screening of dam slopes, considering other impacts of different objective functions on optimization of the dam cross-section.
(1) Stability analysis of the CSG dam slope:
The slope stability of the CSG dam should be checked according to the design specifications of CFRDs by adopting the simplified Bishop method. Considering that the cohesion and friction angle of the CSG material are not constant, the minimum cohesioncand friction angleφwere chosen to be the control parameters, i.e.,c= 443 kPa, andφ= 40.8°. The density of the CSG material was taken asρ= 2 250 kg/m3.
The calculated results show that in the case of the steepest dam slope with the upstream and downstream dam slope ratios ofu=d= 1:0.4, the safety factor of the slope stability obtained using the simplified Bishop method is 4.172, and the safety factor of the slope stability can reach 6.743 while both the upstream and downstream dam slope ratios are 1:1. Thus, it can be seen that the slope stability of the CSG dam is excellent.
(2) Anti-overturning analysis of the CSG dam:
The overturn resistance study was based on the design specification of the RCC dam. The CSG dam is mainly affected by the water load and self-weight load in the storage period. The main cause of overturn of the dam is the non-uniform distribution of the bending moment to the dam toe caused by the water load and the self-weight load of the dam. The ratio of the horizontal component to the total vertical component is the anti-overturning coefficient, which reflects the anti-overturning performance of the dam. As the CSG material has a good performance in water permeability, there is no uplift pressure to be generated at the bottom ofthe dam, which is favorable to the anti-overturning performance of the dam.
The calculated results show that, for the minimum cross-section area (u=d= 1:0.4) of a CSG dam, the anti-overturning coefficient of the whole dam reaches 4.8. With the increase of the area of the dam cross-section, the self-weight of the dam body increases, and the vertical component of the water pressure, which generates an unchanged horizontal thrust on the concrete face, also increases, significantly improving the anti-overturning capacity of the dam. It can be concluded that the CSG dam has significant overturn resistance.
(3) Analysis of the anti-sliding stability of the CSG dam:
As the remarkable decrease of the cross-section area of the CSG dam causes a great reduction of the dam weight, and the steepening of the upstream dam slope reduces the vertical pressure, the anti-sliding stability of the CSG dam will decrease greatly compared with that of an ordinary CFRD. The safety coefficient of anti-sliding stability should be verified for these reasons.
The safety coefficient of anti-sliding stability of the integral dam body can be obtained by the following formula:

whereFsis the safety coefficient of anti-sliding stability of the dam body,fis the coefficient of friction between the dam body and the foundation,ρcis the dry density of the CSG material,ρwis the density of water,hwis the calculated water depth, andθis the upstream dam slope angle. The results are shown in Table 2.
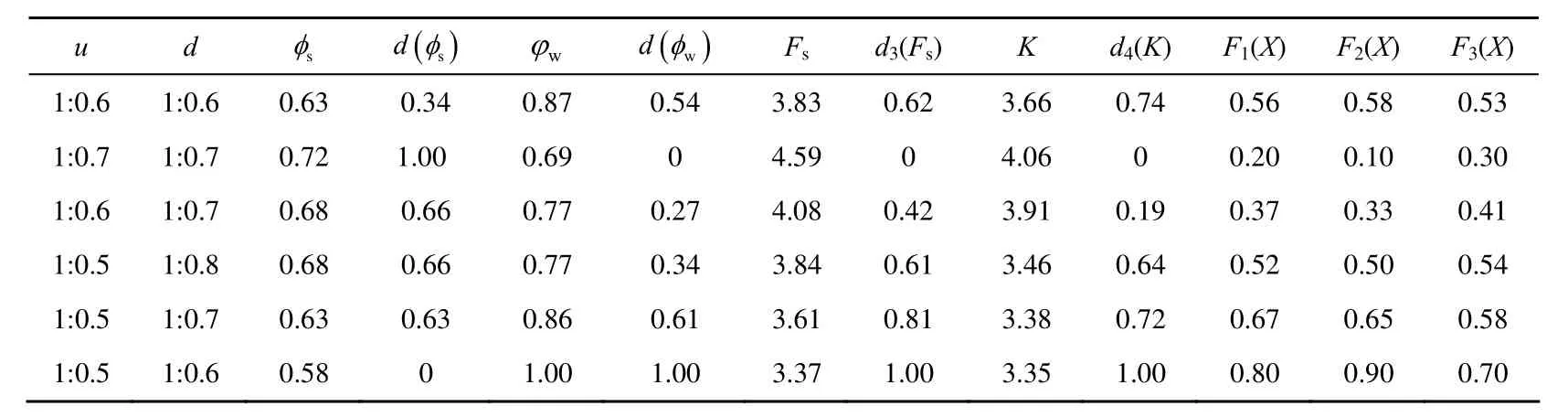
Table 2 Multi-objective optimization results of different dam cross-sections
(4) Analysis of the safety coefficient of the dam strength:
By combination of the overloading method and the strength-reducing method, calculations of cross-sections for six screening dam slope combinations were conducted. The overloading method only overloads the water load by increasing the water density, while the combined method is used to overload the water load by 1.2 times at first, and then to reduce the strength of the CSG material. The safety coefficient of the dam strength can be obtained by the two methods.
For the multi-objective optimization of the CSG dam cross-section, different weight coefficients are needed for different objective functions. There are no criteria for determining the weight coefficient combination. In this study, three kinds of weight coefficient combination schemes were chosen: (1) equal weight selection, (2) inclined to safety weight selection (the value of 0.3 was selected as the weight of the safety coefficient), and (3) inclined to economy weight selection (the value of 0.3 was selected as the weight of the economic coefficient).
The objective function can be obtained from Eq. (8):
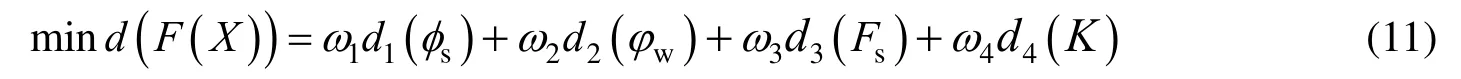
whereKrepresents the safety coefficient of the dam strength.
Based on the analysis above, the economic efficiency, strength, stiffness, and stability of the CSG dam were chosen as objectives to conduct the multi-objective optimization. The results of the analysis of the six dam cross-sections are shown in Table 2.
Table 2 shows that, using the multi-objective optimization method, by making comprehensive analyses of the economic efficiency, the strength safety coefficient, overall stability, and the sensitivity coefficient of the dam displacement to water level changes, we obtained the optimal cross-section under different conditions of weight coefficient combination schemes, and the optimal upstream and downstream dam slope ratios are 1:0.7, consistent with the experiential range of 1:0.6 to 1:0.8 of upstream and downstream dam slopes of the CSG dam determined in previous research (Batmaz 2003; Gurdil and Batmaz 2003; Hirose et al. 2001).
5 Conclusions
This study, conducted with the multi-objective optimization method, involves the comprehensive analysis of the economic efficiency of CSG dams, the sensitivities of the maximum horizontal displacement and the largest settlement of the dam to water level changes, the overall stability, and overall strength security. Further research on 28 dam slop combinations leads to the following conclusions:
(1) The sensitivities of the maximum horizontal displacement and the largest settlement of the dam to the water level change increase with the decrease of the dam cross-section. Meanwhile, the sensitivities increase rapidly as the cross-section decreases to a certain extent (when the upstream and downstream dam slope ratios are greater than 1:0.6).
(2) The maximum horizontal displacement of the dam is much more sensitive than the largest settlement to the water level change, indicating that the horizontal displacement of the dam, while in operation, is greatly affected by the water level, which should be paid more attention to.
(3) The research on the optimization of the CSG dam cross-sections by combining the weight coefficients in three different ways leads to the conclusion that the optimal upstream and downstream dam slope ratios are 1:0.7, consistent with the empirical range of 1:0.6 to1:0.8 of upstream and downstream dam slopes of the CSG dam determined in previous research.
Batmaz, S. 2003. Cindere Dam, 107-m-high roller compacted hardfill dam in Turkey.Proceedings of the 4th International Symposium on Roller Compacted Concrete Dams, 121-126. Lisse: A. A. Balkema.
Cai, X. 2004.Structure Analysis and Optimal Design of Concrete Face Rockfill Dam. Ph. D. Dissertation. Nanjing: Hohai University. (in Chinese)
Cai, X., Shi, J., and Guo, X. W. 2008a. Optimal design of cemented concrete face rockfill dam.Advances in Science and Technology of Water Resources, 28(1), 43-45. (in Chinese)
Cai, X., Wu, Y. L., and Li, G. Y. 2008b. Research on centrifugal model experiment for concrete-faced cemented-rockfill dam.Journal of Hohai University (Natural Sciences), 36(5), 585-589. (in Chinese)
Cai, X., Wu, Y. L., Li, H. X., and Yi, J. G. 2010. Constitutive equation for CSG materials.Chinese Journal of Geotechnical Engineering, 32(9), 1340-1344. (in Chinese)
Dimou, C. K. 2009. Reliability-based optimal design of truss structures using particle swarm optimization.Journal of Computing in Civil Engineering, 23(2), 100-109. [doi:10.1061/(ASCE)0887-3801(2009)23: 2(100)]
Gurdil, A. F., and Batmaz, S. 2003. Structural design of Cindere Dam.Proceedings of the 4th International Symposium on Roller Compacted Concrete Dams, 439-446. Lisse: A. A. Balkema.
Hirose, T, Fujisawa, T, and Nagayama, I. 2001. Design criteria for trapezoid-shaped CSG dams.ICOLD-69th Annual Meeting,Workshop “Modern Techniques for Dams-Financing, Construction, Operation, Risk Assessment”, 457-464. Dresden.
Londe, P., and Lino, M. 1992. The faced symmetrical hardfill dam: A new concept for RCC.Water Power and Dam Construction, 44(2), 19-24.
Luo, Y. S. 2002. Monitoring, operation and maintenance of Chengping Concrete Slab Rockfill Dam.Dam and Safety, (6), 26-29. (in Chinese)
Raphael, J. M. 1970. The optimum gravity dam.Rapid Construction of Concrete Dams, 221-247. New York: ASCE.
Raphael, J. M. 1972. Construction methods for the soil-cement dam.Economical Construction of Concrete Dams, 317. New York: ASCE.
Shi, J. 2006.Research on Structure Analysis and Optimal Design of Cemented Concrete Face Rockfill Dam. M. E. Dissertation. Nanjing: Nanjing Hydraulic Research Institute. (in Chinese)
Wu, Y. L. 2010.Research on Mechanics Feature of CSG Material and Operating Performance of CSG Dam. Ph. D. Dissertation. Nanjing: Hohai University. (in Chinese)
Xie, N. G., Sun, L. S. and Wang, D. X. 2002. Fuzzy multi-objective shape optimization of arch dams.Chinese Journal of Computational Mechanics, 19(2), 192-194. (in Chinese)
This work was supported by the National Natural Science Foundation of China (Grant No. 51179061), and the Specialized Research Fund for the Doctoral Program of Higher Education (Grant No. 20100094110014).
*Corresponding author (e-mail:xcai@hhu.edu.cn)
Received May 18, 2011; accepted Sep. 29, 2011
杂志排行
Water Science and Engineering的其它文章
- Two-dimensional physical habitat modeling of effects of habitat structures on urban stream restoration
- Experimental study on total dissolved gas supersaturation in water
- Hydrodynamic effects of reconnecting lake group with Yangtze River in China
- Sediment transport following water transfer from Yangtze River to Taihu Basin
- Analysis of black water aggregation in Taihu Lake
- Large eddy simulation of water flow over series of dunes
