襟翼对垂直轴风力机性能影响的数值模拟

徐 璋, 王 茜, 皇甫凯林, 钟英杰

(浙江工业大学能源与动力工程研究所,杭州 310014)

三叶片直翼式垂直轴风力机出力效率受到叶片个数、实度、尖速比以及风力机半径等因素的影响,科研人员在进行设计参数对垂直轴风力机性能影响的研究中证实:该型风力机在某一区域内存在一个最佳尖速比[1],它能使风力机的功率系数达到最大.作为风力机重要气动部件之一的叶片,在翼尾加装格尼(Gurney)襟翼是一种能够提高桨叶升力的既简单又经济的方法[2-3].在水平轴风力机加装Gurney襟翼能提高风力机的风能利用系数[4],但在垂直轴风力机上加装襟翼的研究并不多见.因此,笔者以垂直轴风力机为对象,在Gurney襟翼的基础上研究了在风力机翼尾加装襟翼后的气动特性和桨叶升力的提高.

对于直翼式垂直轴风力机,可以对垂直于风力机截面的一个平面进行二维数值模拟[5].随着滑移网格技术的发展,应用滑移网格技术对直叶片垂直轴风力机整机进行非定常的数值模拟,能够较好地反映该型风力机的流场特性[6].滑移网络技术不要求交界面两侧的网格点相互重合,可以使两侧的网格相互滑动,当每个时间步迭代结束后,整个滑动区域按指定的方式移动,因此可以真实地模拟风力机转子与定子间的相互影响.

笔者先采用滑移网格技术对未加装襟翼的“原型”风力机NACA0015翼型进行二维非定常数值模拟并研究了该型号三叶片风力机整机最大功率系数时的尖速比;然后,在原型的基础上对该风力机机翼加装高度为2%C(C为翼型弦长)的襟翼,对相同高度下4种不同形状的襟翼改型,跟踪风力机叶片在一个完整的旋转周期中处于不同尖速比、旋转角度下的转矩系数和功率系数作进一步研究,得到各种襟翼改型的适用性,为风力机翼型改型提供参考.

1 模型和方法

1.1 几何模型的建立

风力机为三叶片垂直轴直翼式.为减少周围流场对风机的影响,需保证计算域足够大,因此笔者选取计算区域x=-5d～15d,y=-5d～5d,d—风力机直径,m.图1为风力机的整体计算域.

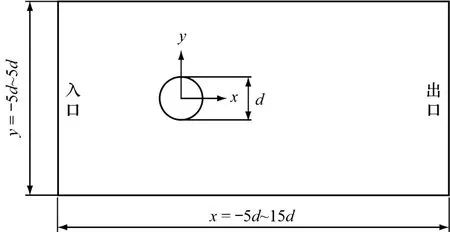
图1 风力机的整体计算域Fig.1 Overall computational domain of wind turbine

为降低计算过程中对计算机内存的需求并保证较好的网格质量,流场采用分块耦合求解,并对风力机叶片附近网格进行了加密处理,而且设置了边界层.整个流场区域采用结构形式网格划分,各固壁面无滑移、无渗透.同时,为了便于网格建立,此处的网格划分忽略了风力机转轴以及支臂的影响.

风力机在旋转过程中,风轮每转动一个角度,叶片所在位置即发生变化,其相对速度和攻角均随之变化,从而影响流场的变化.流动是非定常的,在转子与定子间的相互影响不可忽略的情况下,可采用滑移网格模型来处理其相互作用随时间的变化.但是,在采用滑移网格模型计算时,计算量非常大,特别是在涉及复杂几何边界的高雷诺数区域流动时,大约有70%的网格点位于只占计算域10%的近壁区[7],因此在保证计算精度的同时选取合适的网格数量十分必要.风轮附近区域网格加密划分后的环形滑移域与翼型网格局部网格放大示于图2和图3.网格总数在25万左右,因加装襟翼高度和形状的不同,网格总数稍有变化.

图2 环形滑移域Fig.2 Slip ring domain

图3 NACA0015翼型网格局部放大Fig.3 Partial enlargement of NACA0015 airfoil mesh

1.2 控制方程和边界条件

对于直叶片垂直轴风力机,除去叶尖外,绝大部分叶片横截面流场相似,因此可近似地把三维流场简化为二维流场,使计算量大为减少.所以,控制方程采用不考虑体积力和外部热源的二维非定常不可压缩N-S方程.

边界条件为:左侧进口和上下侧面采用速度进口边界U∞=8 m/s,右侧出口为压力出口边界.NACA0015翼型:直径 d=2.5 m,弦长C=150 mm,弦长雷诺数Re为:

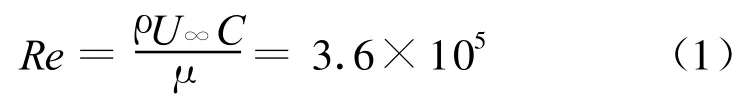
实度σ为:

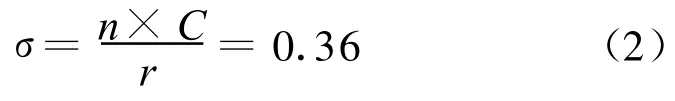
式中:n为叶片个数;r为风力机风轮半径;μ为介质黏度系数;ρ为空气密度.

翼型表面定义为无滑移的绝热固壁边界,通过控制旋转滑移域的旋转角速度来控制风力机的尖速比变化.

1.3 湍流模型和计算方法

湍流模型采用DES模型.DES方法由Spalart提出,它是把大涡模拟与常规的雷诺平均N-S方程的优点结合起来数值模拟带脱体涡的一种新方法.它在物面附近采用RANS方法,在其他区域则采用Smagorinski大涡模拟(LES)方法,因此该方法是一种混合解法.

速度和压力耦合采用Simple算法,动量方程采用Bounded central differencing离散格式,湍流黏度采用二阶迎风格式.根据不同的尖速比来选定非定常计算采用的时间步长,在初始计算时采用较大的时间步长以便较快地算出初始阶段风力机叶轮加速的流场,然后减小每次计算的时间步长,使风力机每个时间步长旋转的角度等于5°,由此确定的时间步长约为0.005 s.根据转速,可计算出完成一个周期旋转所需的时间步长数.

在计算时,要求每步迭代计算皆达到内部收敛,所有流场参数也应达到相应格式的收敛,以保证数值解的精度.在计算过程中,需监测翼型的转矩系数变化,当每周期的转矩系数曲线已不再变化或变化很小时(小于5%),即可认为流场收敛.另外,为保证整个计算域流场的计算准确,充分的计算时间是必要的,本文的所有非定常流场工况计算得到稳定结果所需时间为6～8 h,每个流场中的运行时间(flow time)均超过5 s.

图4为风力机转动时的风轮旋转示意图.在图4中,U∞为计算域来流边界上的风速;ω为风轮运转时的角速度;θ定义为风力机叶片1距离初始位置(y轴正向)的旋转角度;尖速比λ=ω r/U∞.

为了解风力机叶轮在运转过程中的空气动力学特性,要监测转矩系数Ct和功率系数CP变化,其定义如下:

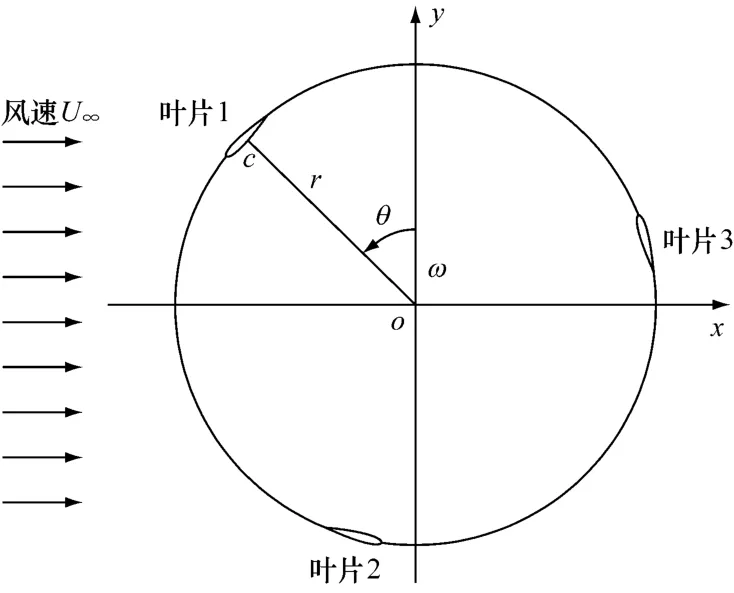
图4 风力机风轮旋转示意图Fig.4 Schematic diagram of wind turbine rotation

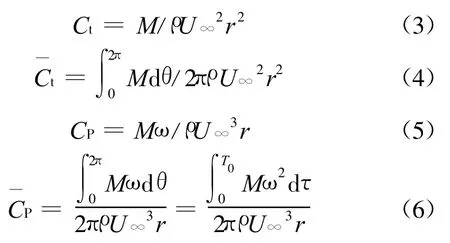
1.4 结果验证和分析

对采用NACA0015翼型的三叶片直翼式风力机整机,计算出叶片1在一个周期内的转矩系数和功率系数随尖速比的变化(图5).

从图5(a)可知:风轮在旋转过程中,由于尖速比的不同和入流角的不断变化,转矩系数呈抛物线变化,与杨从新等[1]采用Matlab软件和试验相结合的方法进行的研究结果相符.除0°和 180°相对风速不产生升力外,叶片在其他位置受到的升力均能在运动方向产生转矩力,这符合达里厄风力机在风力下旋转的原理.从图5还可看到:由于阻力相对于风轮产生的力矩是负的,当叶片的尖速比较小(λ=2)时,叶片基本上不产生推动风轮旋转的力,反而在大部分区间阻碍风轮转动;在较高的叶片尖速比(λ=3～5)下,转矩输出的峰值出现在叶片旋转角90°附近,随着尖速比的增大,最大转矩出现的时间向后推迟.叶片的最大出力范围为迎风方向0～180°,即上半程,叶片后半程的出力明显下降.另外,转矩系数的峰值随尖速比增大而略有下降,这主要是因为随着风力机叶轮转速的提高,它将受到圆柱效应[8]的影响,导致风速在风力机内部明显衰减.

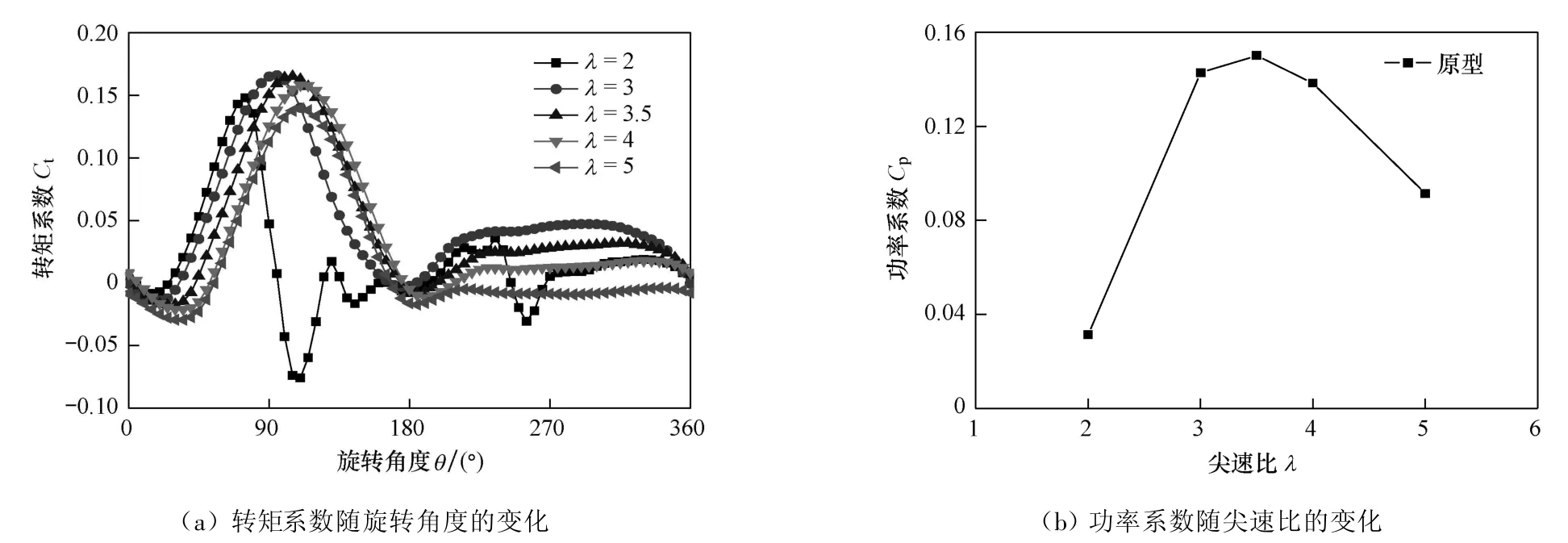
图5 单个叶片在一个周期内转矩系数和功率系数随尖速比的变化Fig.5 Torque and power coefficient of single blade varying with tip-speed ratio in a cy cle

为了确定出该种型号的风力机处于最大功率下的尖速比,笔者对模拟结果进行了数学换算.从图5(b)可看出:风力机在尖速比3.5左右时功率输出达到最大值,之后随着风机转速的提高,输出功率反而下降.这与杨丛新等[1]对NACA0012翼型的研究结果一致.

2 尾部改型

Gurney襟翼是在翼型尾部的下表面加装1个高度很小、厚度也很小的片状增升装置.在加装襟翼高度方面的研究中,Liebeck[8]研究Gurney襟翼时得出:当襟翼高度不超过弦长的2%时不会带来阻力的显著增加;同时Myose等[9]在对 NACA0011翼型的风洞测试结果表明:0°攻角下该翼型尾缘处的边界层厚度大约为弦长的 1.5%.相对于NACA0011翼型,NACA0015的翼型尺寸更厚,所以其尾缘处的边界层厚度也会有所增加.所以,实际加装的Gurney襟翼高度值不能太大,应使其位于边界层内,这样就不能将襟翼当作突起物,其存在也不会对流动产生太大的不利影响而引起阻力的显著增加.根据空气动力学理论,突然变化的襟翼会在运行中产生较大的阻力,尾部削平后保持近似流线的形状有助于减小这一影响,因此笔者在研究尾部改型对风力机功率的影响时作出了高度为2%弦长、宽度2 mm的内外2种Gurney襟翼,以及在此基础上进行流线处理的两种新形式.NACA0015直翼式垂直轴风力机尾部改型示意图见表1.

3 转矩系数和功率系数

图6为2%弦长襟翼系列与NACA0015原型转矩系数和功率系数的对比.从图6(a)可知:风力机在最大功率(尖速比λ=3.5)工况下,两种流线型襟翼外峰值有所下降,阻力减小均有所改善.与原型相比,外侧的襟翼增加了叶片在0°～180°的转矩输出,而在180°～360°时,由于襟翼的存在导致风力机的运行阻力增加而使转矩输出小于原型;内侧的襟翼与此相反,在后半程的转矩输出大于原型.

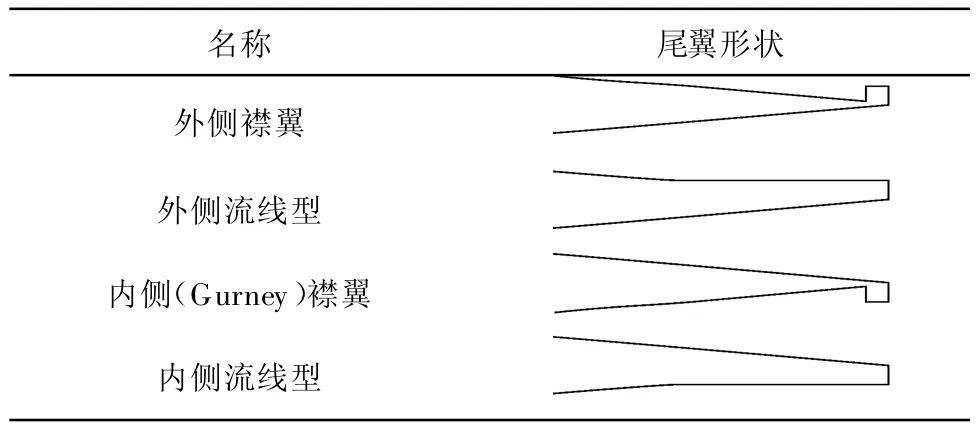
表12 %C襟翼系列尾部改型示意图Tab.1 Schematic diagram of various 2%C flap modifications

风力机的输出功率除峰值功率外还需要了解各改型的总体效果,因此以原型为参照比较了各尾部改型的功率系数随尖速比的变化,如图6(b)所示.从图6(b)可以看出:在低尖速比(λ=2或 λ=3)工况下,加装Gurney襟翼的风力机输出功率明显大于其他形式襟翼下的风力机,最大功率比原型提高了4.03%;内侧流线型襟翼的输出功率比原型提高了约3%.另外,虽然外侧流线型襟翼比外侧襟翼输出功率提高7.14%,但是外侧襟翼在低尖速比时功率远低于原型.随着尖速比的提高,尖速比λ大于3.5以后,经过处理的流线型襟翼对降低阻力起到了一定作用.因为垂直轴风力机叶片在旋转一周的过程中,随着攻角的增大,升力和升阻比都将经历一个先增后减的过程,这主要由于阻力也会随着攻角的增大而增加,因此图6(b)中加装襟翼后的风力机输出功率小于原型.

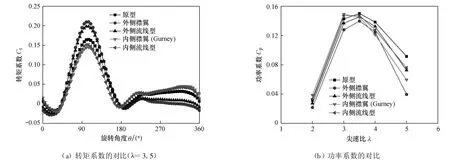
图6 2%弦长襟翼系列与NACA0015原型转矩系数和功率系数的对比Fig.6 Comparison of torque and power coefficient between 2%chord flap series and NACA0015 prototype

4 结 论

(1)NACA0015三叶片直翼式垂直轴风力机在尖速比约为3.5时的输出功率最大,当超过此尖速比时风力机的输出功率反而下降.

(2)在风力机原型上加装高度为2%弦长的襟翼,与原型对比后发现:在低尖速比时,适合采用内侧襟翼,Gurney襟翼的输出功率最大可提高约4%,内侧流线型襟翼提高的幅度略低.当尖速比提高到4以后,由于尾部突起增大了风力机在高速运转时的阻力,因此在风力机叶片上加装襟翼反而会降低垂直轴风力机的输出功率.

(3)根据尖速比的定义,尖速比与来流风速成反比,因此对于高尖速比(低风速)时出现的采用风力机原型更具优势的情况,可以通过一定的装置把风力机叶片尾翼的襟翼收起,以获得较大的输出功率.但是,鉴于数值模拟对同一模型结构改变时模拟连贯性的限制,这种操作需要先在风洞中进行试验,经过进一步验证其实际效果后再加以实施.

[1]杨从新,巫发明,王立鹏,等.设计参数对直叶片垂直轴风力机功率系数的影响[J].兰州理工大学学报,2009,35(5):47-50.YANG Congxin,WU Faming,WANG Lipeng,et al.Effect of design parameters on power coefficient of a straight-bladed vertical-axis wind turbine[J].Journal of Lanzhou University of Technology,2009,35(5):47-50.

[2]张宏武,江学忠,袁新,等.二维翼型襟翼增升的数值模拟[J].清华大学学报:自然科学版,2000,40(11):55-58.ZHANG Hongwu,JIANG Xuezhong,YUAN Xin,et al.Numerical simulation of 2D airfoil lift enhancement with flaps[J].Journal of Tsinghua University:Science and Technology,2000,40(11):55-58.

[3]苏明军,李文华.风力机二维翼型Gurney襟翼增升的数值模拟[J].可再生能源,2007,25(2):60-62.SU Mingjun,LI Wenhua.Numerical simulation on lift enhancement of 2D aerofoil Gurney flaps of wind turbine[J].Renewable Energy Resources,2007,25(2):60-62.

[4]申振华,于国亮.翼型弯度对风力机性能的影响[J].动力工程,2007,27(1):136-139.SHEN Zhenhua,YU Guoliang.Influence of airfoils camber on the performance of wind turbines[J].Journal of Power Engineering,2007,27(1):136-139.

[5]JIANG Zhichao,DOIYasuaki,ZHANG Shuyou.Numerical investigation on the flow and power of small-sized multi-bladed straight Darrieus wind turbine[J].Journal of Zhejiang University:Science A,2007,8(9):1414-1421.

[6]杨从新,巫发明,张玉良.基于滑移网格的垂直轴风力机非定常数值模拟[J].农业机械学报,2009,40(6):98-102.YANG Congxin,WUFaming,ZHANGYuliang.Numerical simulation on unsteady rotated flow of a vertical axis wind turbine based on moving meshes[J].Transactions of the Chinese Society for Agriculture Machinery,2009,40(6):98-102.

[7]张兆顺,崔桂香,许春晓.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社,2008.

[8]LIEBECK R H.Design of subsonic airfoils for high lift[J].Journal of Aircraft,1978,15(9):547-561.

[9]MYOSE R,HERON I,PAPADAKIS M.The poststall effect of Gurney flaps on a NACA 0011airfoil[C]//Aerospace Atlantic Conference&Exposition.Dayton,USA:1996.