三维曲面的纹理映射失真修复算法的研究

2011-08-14张跃安娜

电大理工 2011年3期

张跃安娜

1,2沈阳师范大学（110034） 1辽宁装备制造职业技术学院（沈阳 110164 ）

纹理映射技术可将任意的平面图形或图像覆盖到几何模型的表面上，在模型表面形成逼真的色彩花纹。本文讨论的纹理映射失真修复的方法主要是针对三维地形，在保持地形曲面不变的前提下，对每个三角形给出了纹理失真的度量方法及失真修复的方法。

1 纹理失真的原因

在一个加了纹理的三角网模型中，三角形的每个顶点都记录了三维几何空间中的几何坐标vg和纹理空间中的纹理坐标vt，在给模型进行纹理映射时，三角形内部的纹理坐标可以根据三个顶点的纹理坐标值进行插值来得到。图1给出一个实际模型的例子来说明纹理失真的形成，图1(a)中三角形的顶点v1g，v2g，v3g分别对应了图1(b)中的v1t，v2t，v3t。所以最后的纹理映射结果如图1(c)所示。从图中可以看出，纹理图像上的直角三角形对应了一个几何空间中的非直角三角形，纹理图案在纹理映射过程中发生了形变。由于纹理图像是二维的，物体模型是三维的，这就导致模型上大小相似的三角形，某些对应了较大的纹理，某些对应了一些小块的纹理，所以导致了纹理的失真。

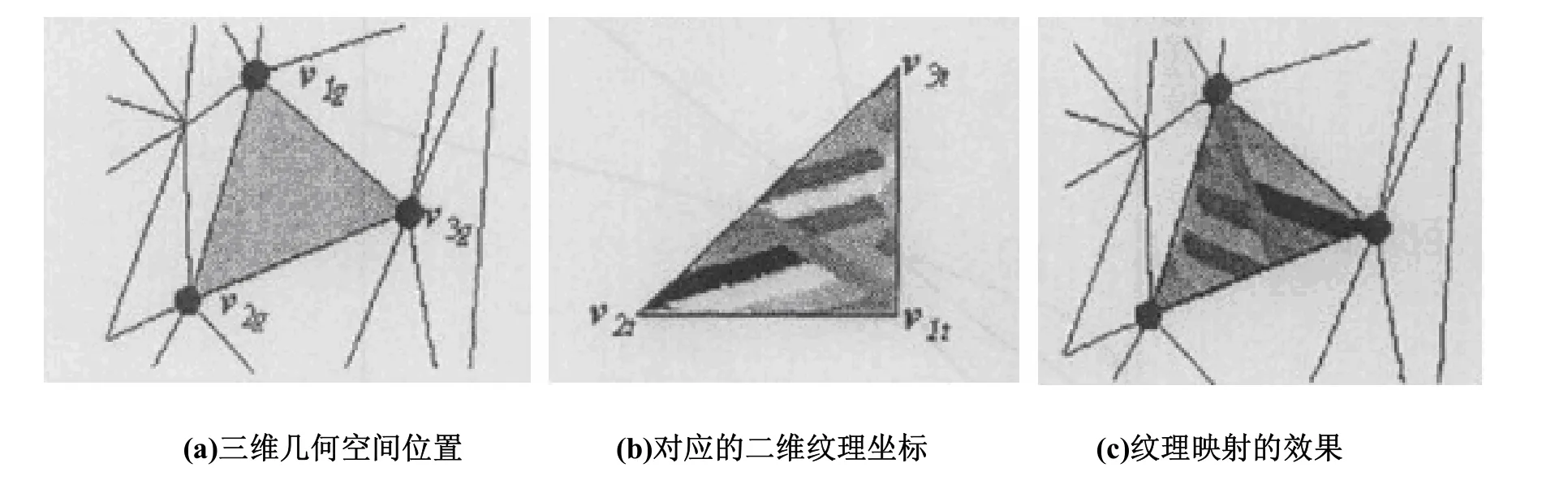
图1 三角形纹理失真的过程

2 纹理失真修复算法

关于三维地形纹理映射过程中所产生的失真情况较少有人研究，试图从纠正失真不均衡的角度出发对纹理映射后失真纹理进行修复。纹理失真修复的算法主要有纹理重投影和结合纹理特征的模型简化算法。而采用的算法主要针对三维地形曲面上的纹理进行修复，算法主要分为纹理失真系数的确定、失真大小的向量度量方法、投影平面上点的平移方法3个步骤。

2.1 纹理失真系数的确定

在对三角网模型进行纹理映射时，先将空间的三角网格投影到二维平面上，得到投影平面上的三角网模型，这样投影平面上的每一个三角形都对应着空间三角网中的一个三角形。对于失真系数的确定，首先选取投影平面上三角形的重心，然后做平行于X、Y轴的直线与三角形的两边相交得到一截线段，称为投影截线段，再找到投影截线段在空间三角网中所对应的线段，我们称为空间截线段。则空间截线段与投影截线段的长度的比值，称为失真系数。而失真系数与 1的差值就是此三角形的失真增量。这样针对每个三角形都可以求出 X,Y方向二个失真系数，作为对这个三角形X,Y两个方向失真的度量方法。

2.2 失真大小的向量度量方法

由于失真系数和失真增量是一个标量，所以无法根据失真系数确定投影平面上三角形的失真方向，也就无法挪动点来对失真进行修复。但是根据投影平面上三角形在X轴、Y轴两个方向上的失真增量，在二维直角坐标系中可以确定四个方向向量K1，K2，K3，K4，如图2所示。把这四个方向中的一个称为失真向量。为了给出失真向量的方向，我们过投影平面三角形的检索点(要挪动的点)做其对边的平行向量，这里把B点作为检索点，EF为平行向量，由于失真是投影平面的三角形被拉伸造成的，则可排除平行向量EF与 B点的对边AC所夹的两个方向向量K1，K4。再取检索点B对边AC的中点P，由P和检索点B可确定一个由B到P的向量我们称其为中点向量BP，判断另两个方向向量K2，K3与中点向量 BP的夹角大小，选取与中点向量BP的夹角较小的方向向量 K3为失真向量的方向，而失真向量的大小即为失真增量与中点向量模长的乘积。每个检索点对应每个三角形都有唯一的失真向量，这个失真向量就代表这个三角形的失真程度，也代表检索点在投影平面上点的挪动方式。

图2 失真向量的确定

2.3 投影平面上点的挪动方法

确定了投影平面上各个三角形失真向量的大小和方向后，对于投影平面上的任一检索点都可以求出与此检索点相关的所有三角形的失真向量，再对每一个失真向量在X和Y方向进行矢量分解，求出X方向上的总的矢量和，Y方向上总的矢量和。最终得到X和Y两个方向上的向量，分别称其为X方向平移向量和Y方向平移向量，平移向量的方向即为检索点的移动方向，平移向量的大小即为检索点移动的距离。如图3所示，点B就是三角网中的一个检索点，在它周围有5个三角形，求出B点关于这五个三角形的失真向量，然后X，Y方向进行分解，在做矢量和，求出B点X，Y方向平移向量，就是 B点要挪动的方向和距离。然后对挪动后的平面重新进行纹理映射，就可以得到比较均衡的纹理图片。

图3 点的挪动

3 结论

这种算法针对三维地形中每个三角形给出了失真系数的确定以及失真大小的向量度量方法，解决了一定的纹理失真问题，修复后的图片纹理比较均匀，能比较好的刻画纹理的细部特征。但是本文中只是针对三维地形中DEM模型进行了纹理失真的修复，也存在一定的局限性。如果能加以扩展，将有更广的应用价值。图4、图5为修复前和修复后的图片。