基于层次-效用法的空中目标威胁度判断模型
2011-08-14周鹏文蒋里强
周鹏文,蒋里强
(防空兵指挥学院,河南 郑州 450052)
1 引言
在现代防空作战中,敌机来袭的特点多半是小间隔、多批次、全方位、连续袭击,而防空一方由于兵力较少、地位被动,难以做到对所有的敌机都进行有效的抗击。这就要求指挥员对来袭敌机的威胁度做出准确的判断,而后按照先大后小的顺序逐次进行抗击。过去,指挥员都是凭借以往的作战经验来定性地分析来袭敌机的威胁度,这种方法在信息化条件下的现代防空作战中很容易造成失误。针对敌现代空袭呈现出的新样式、新手段和新特点,我们可以利用模糊灰色方法中的层次-效用法,对来袭目标的威胁度进行定量分析,准确判断来袭目标的威胁度,为防空一方的指挥员合理、准确地运用火力提供科学依据。
2 模型假设
设有n批来袭目标,影响每批目标对我掩护目标威胁度的主要指标因素有m个,如:掩护的性质、机型、架数、批次、高度、距离、飞临时间、航路捷径和来袭方向等因素(不考虑指挥员的主观决策因素)。
3 模型的建立
3.1 利用AHP层次分析法来建立层次结构
m个指标因素对威胁度影响的权重向量W=(W1,W2,…,Wm)T可通过 AHP层次分析法求出,其层次结构(以目标防空为例)如图1所示。
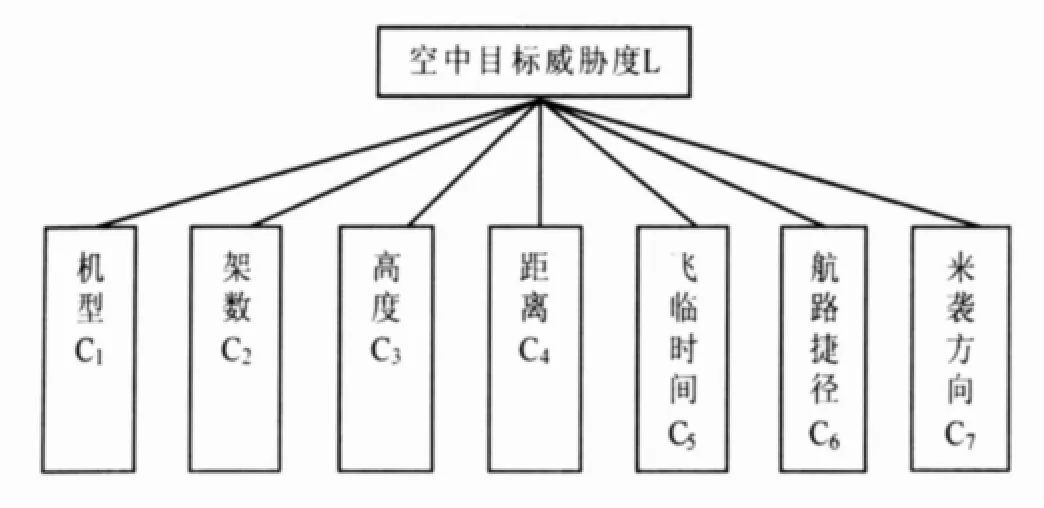
图1 层次结构图
3.2 构造判断矩阵
以L表示目标,Ci(i=1,2,…,7)表示指标因素,Ci∈C(设集合 C={Ci|i=1,2,…,7}),βij表示 Ci对 Cj的相对重要性数值 (i,j=1,2,…,7),βij的取值依据判断矩阵标度及其含义确定。
根据判断矩阵标度及其含义,通过征求专家意见,可得L-C判断矩阵:
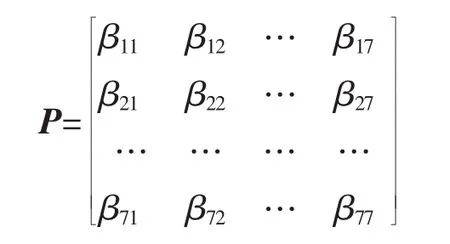
3.3 求判断矩阵的特征向量
采用方根法,根据L-C判断矩阵,求出最大特征根所对应的特征向量,所求特征向量即为诸因素 Ci(i=1,2,…,7) 的权数分配 αi(i=1,2,…,7)。
a)计算L-C矩阵每一行元素的乘积Mi
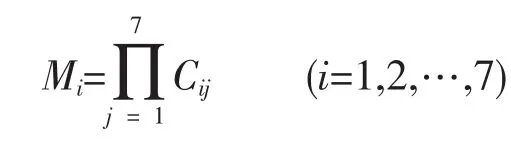
b)计算Mi的7次根
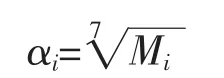
W=(W1,W2,…,Wm)T=(α1,α2,…,α7)T即为所求特征向量。
3.4 判断矩阵的一致性检验
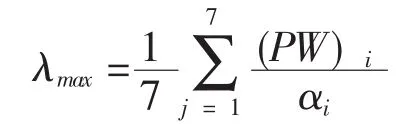
式中 (PW)i表示向量PW的第i个元素,而
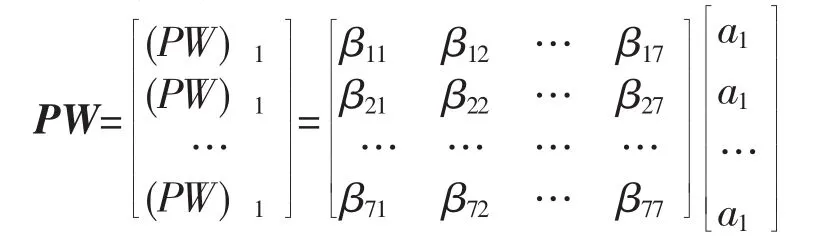
PI被称为判断矩阵的平均随机一致性指标。
当时CR<0.10,即认为判断矩阵具有满意的一致性,说明权数分配是合理的;否则,就需要调整判断矩阵,直到取得具有满意的一致性为止。
3.5 计算指标因素的效用函数
第Li(i=1,2,…,n)目标的第j个指标因素Cj(j=1,2,…,m) 的数据为 βij,其矩阵为 B=(βij)n×m,。
a)若指标因素Cj越大,对威胁度的影响越大,则Cj采用的效用函数为:
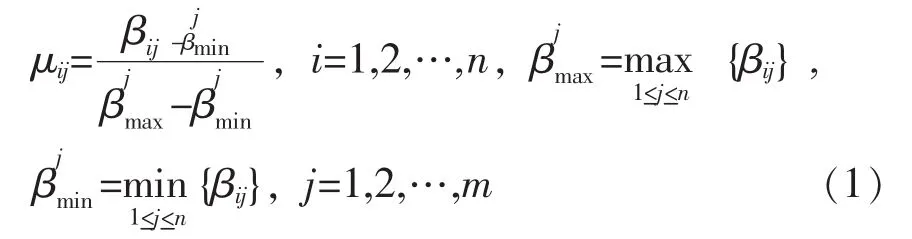
b)若指标因素Cj越小,对威胁度影响越大,则Cj采用的效用函数为:
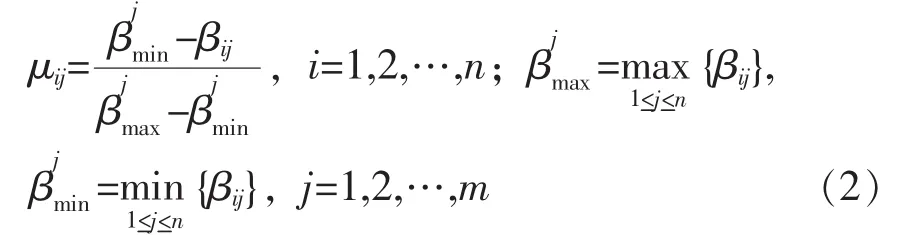
c)若指标因素Cj越接近某给定值β*,对威胁度的影响越大,则Cj采用的效用函数为:
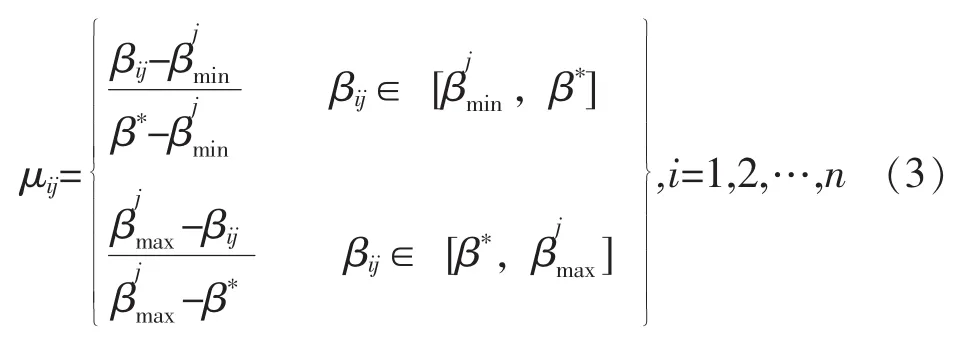
则n批来袭目标的m个影响威胁度的指标因素的效用函数构成矩阵 μ=(μij)n×m。
3.6 威胁度计算并排序
根据前面AHP层次分析法已计算得Cj(j=1,2,…,m)的权重向量W=(W1,W2,…,Wm)T,则第Li批(i=1,2,…,m)的威胁度就可用综合量化值Ei表示:
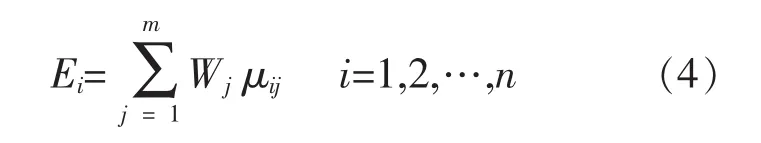
最后对 {Ei} (i=1,2,…,n)由大到小进行排序,就可得出n批空中目标中不同威胁度的批次顺序。
4 实例分析
某防空兵群掩护一目标对空安全,现有4批空中目标接近和进入分配环带,来袭目标的各种有关数值如表1所示,群判断敌机主攻方向为正东(15—00),在火力分配前,计算出各批目标的威胁度并排序。
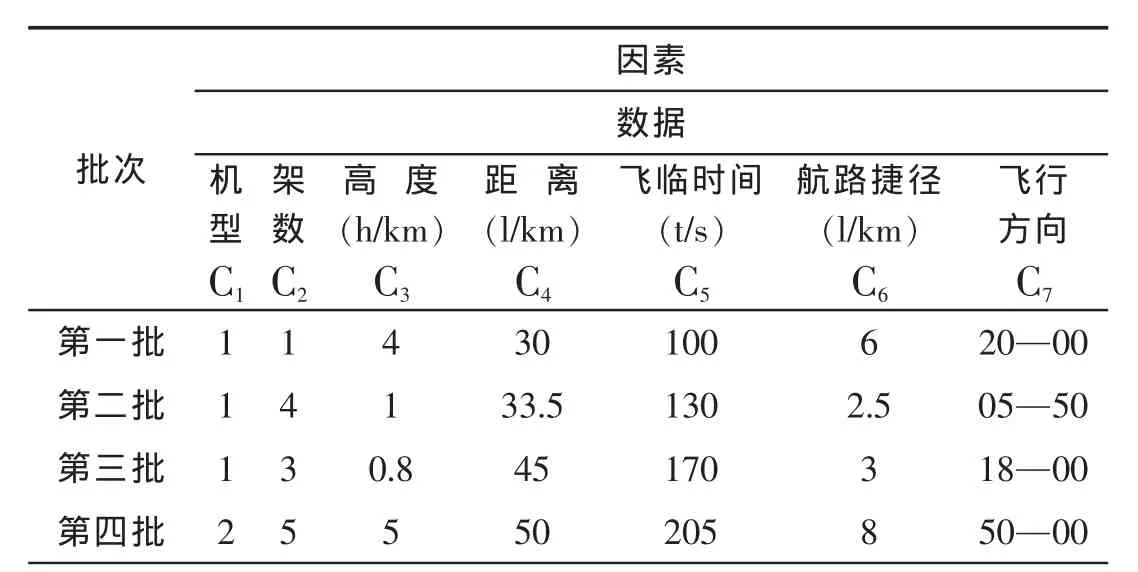
表1 平袭目标的各种数值
解:a)利用AHP层次分析法确定指标因素的权重W,建立L—C层判断矩阵如表2所示。
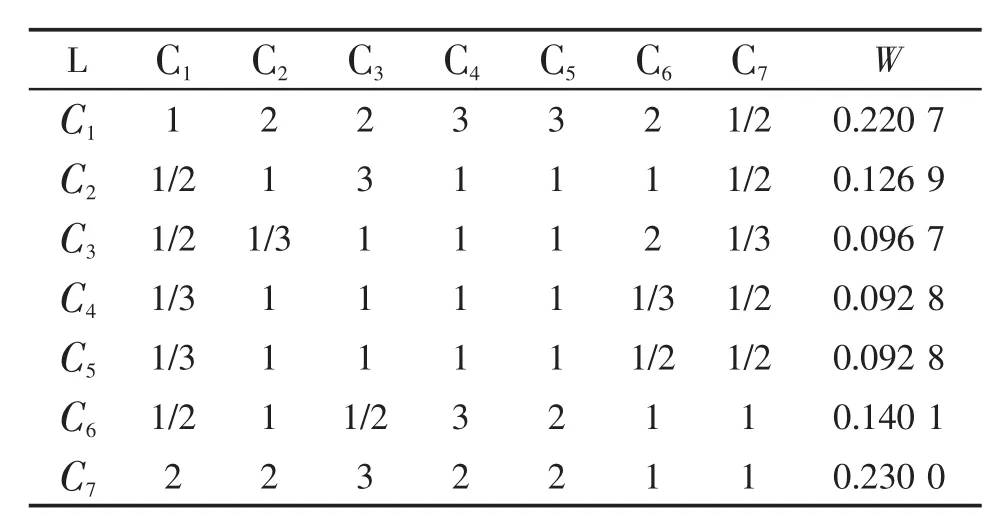
表2 L—C层判断矩阵
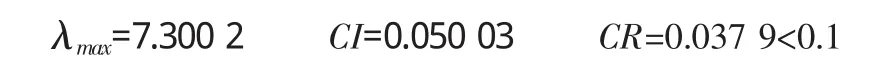
b)选用公式(1)、(2)和(3)计算表1的效用函数值,结果如表3所示。
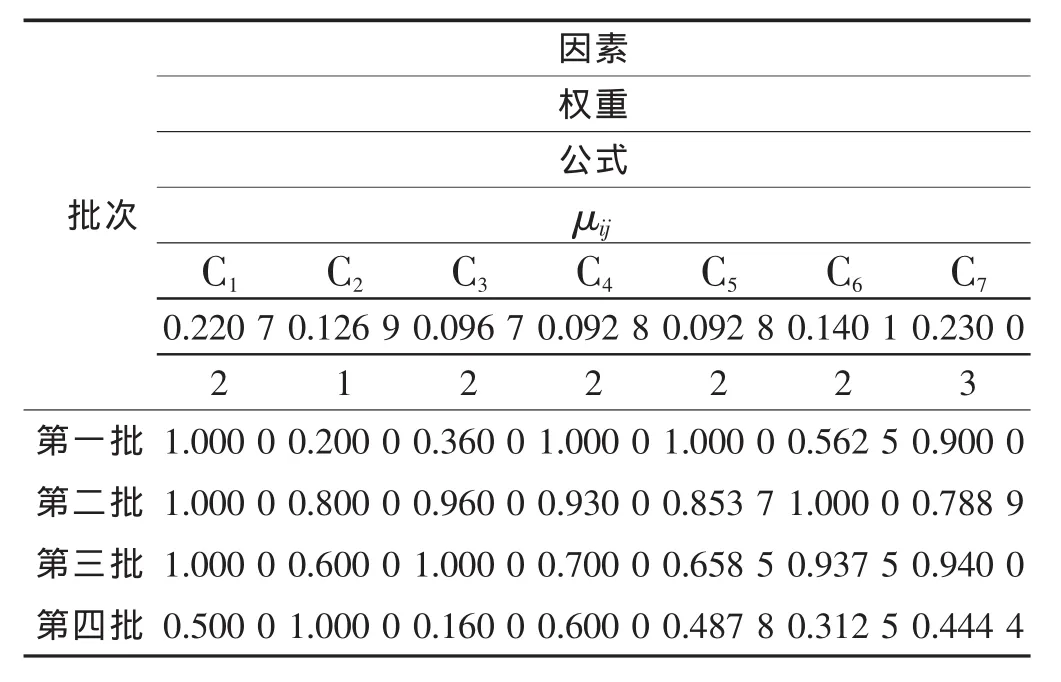
表3 效用函数值
c)根据式(1)-(4)计算各批次威胁度,结果如表4所示。
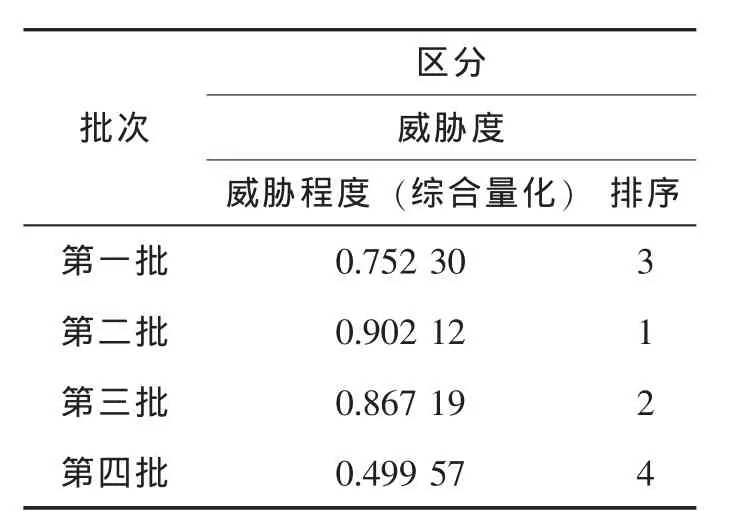
表4 各批次威胁度结果
从表4可知,第二批目标的威胁度最大,第三批目标为第二,第一批目标为第三,第四批目标为第四,这同实际作战过程中指挥员的经验判断相吻合。
4 结束语
在AHP层次分析法的基础上,用指标因素的效用函数法来计算空中目标的威胁度,可以使复杂问题条理化,并对各效用函数进行加权和线性变换,得到综合量化值即威胁度,使得各指标因素对威胁度影响得到较合理的体现。因此,其求解方法及排序能够较好地反映作战的实际情况,对指挥员准确、合理运用火力具有一定的可信度和参考性。
[1]郝 强,张树德.模糊灰色方法在防空兵作战分析中的应用[M].郑州:军事科学出版社,1997.
[2]谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中科技大学出版社,2005.
[3]朱雪平.陆军战役军团防空兵作战资源需求理论研究[M].北京:海潮出版社,2008.
[4]蒋里强,左毅.防空兵作战模拟方法概论[M].北京:海潮出版社,2009.
