论证军用装备RMS顶层参数指标的意义和建议
2011-08-14丁定浩
丁定浩
(中国电子科技集团公司电子科学研究院,北京 100041)
1 引言
新研军用装备在寿命周期内持续保持满足使用需求的保障概率,必须要由可靠性、维修性、备件保障性有机地组合来保证,任一可靠性、维修性、备件保障性的单项参数,都无法保障装备整体全寿命周期持续保持满足使用需求保障概率要求的实现。
但在当前,RMS参数指标都是以单项参数指标要求提出的。通常见到的是装备任务可靠度或平均致命故障间隔时间(MTBCF)、装备基本可靠度或平均故障间隔时间(MTBF)、平均修复时间(MTTR),以及故障检测率、故障隔离率、虚警率等测试性指标。缺乏一个定量的、总体的、保证在寿命周期内能持续保持正常使用的概率指标。也说是说,一方面,这些任务可靠度、基本可靠度、平均修复时间、故障检测率、隔离率和虚警率的集合,还说不清楚它们保障装备在整个寿命周期内能实际持续保证正常使用到底有多高的概率。
另一方面,对于上述这些可靠性、维修性、测试性和保障性等参数所确定的量值,为什么是这一数值,而不是其它数值,通常也提不出确切的根据。多半是参考、参照、抄袭得出的,说不清楚它们之间定量的相互关系。例如:任务可靠度指标,它只能说明在一个任务持续时间内不发生致命故障的概率,要它在整个寿命周期内持续保持任务可靠度的实现,无疑要有相应的维修保障和备件保障为前提。但要有多高的维修能力和多少备件配置及其补充方式,任务可靠度指标本身是无法回答的。单项的维修性指标也不能回答这一问题。至于备件保障,特别是系统的备件保障,迄今尚未见到可以实际设计操作的系列解析模型。
因此,研究到底应该提出什么参数指标,并如何定量地确定这些参数指标,既能保障寿命周期定量的使用需求,又能降低寿命周期费用,都是长期试图解决但迄今没有得到满意解决的课题,这是论证确定RMS参数指标的初衷和目的。
2 根据任务剖面来确定RMS的顶层参数指标的类型
RMS顶层参数指标的类型,取决于任务剖面中的工作方式。这里所指任务剖面的不同工作方式,就是要区分是日以继夜连续工作方式,还是工作、停机交替进行的间断工作方式。
对于日以继夜连续工作方式的RMS顶层参数,无疑是使用可用度参数。使用可用度模型中包含了可靠性、维修性和备件保障性参数,模型中的可靠性参数是以平均工作时间(MUT)表示的,维修性参数是以平均修复时间(MTTR)和预防维修参数以平均预防维修时间(MTTPM)表达的,备件保障性参数是以平均延误时间(MLDT)表示的。这一模型是从连续工作状态马尔柯夫随机过程中导出的。使用可用度AO模型是它的动态平衡状态的概率,即:

但这一模型仅适用于串联结构和停机检修的冗余结构,而在连续工作任务剖面中,停机检修的冗余结构通常是不用的,原因是可用度不升反而降低。上列模型对联机检修的冗余结构则须要加以修正。原因是在联机检修状态下的平均工作时间与平均备件延误时间有关,式中仅考虑平均备件延误时间对停机时间的影响,没有考虑它对平均工作时间的影响,对此,笔者将另文推导,给出修正模型。
对于工作、停机交替进行的间断工作方式,其RMS的顶层参数具有两种不同的类型,这就是任务成功率和能执行任务率。任务成功率是针对以任务成功与失效次数描述的全寿命周期中持续保持任务成功的概率;能执行任务率是针对全寿命周期中持续保持实际能工作的时间与要求工作时间之比,是要求工作时间的利用率。它与连续工作任务剖面中的使用可用度相当。
新的任务成功率模型、能执行任务率模型已经导出[1-2],它们分别是:
任务成功率PSM的模型为:

能执行任务率MCR的模型为:

式(2)、(3)中:ts——任务持续工作时间;
td——两次任务之间的后勤保障停机时间;
RS(ts)——任务可靠度;

以可靠性、维修性、备件保障性为变量的系统RMS顶层参数函数模型的确立,是论证顶层参数指标的前提。
由此可以确定各项单项参数与顶层参数之间的定量关系,各项单项参数与顶层参数和其它单项参数之间的定量关系。
3 根据能接受最大风险概率来确定顶层参数指标的量值
如何定量地确定RMS顶层参数指标的量值,是参数指标论证的要求之二,论证的内涵就是它的定量的需求性与可行性。论证需求概率多高,或者论证相对比较直观的、可以接受的风险概率。顶层参数指标的需求概率,无疑就是风险概率的对立概率。
根据装备用途的不同,存在不同的风险概率指标:1)安全风险概率指标;2)任务风险概率指标。安全性涉及机毁人亡的风险,任务风险涉及任务失败的风险。
在通常情况下,涉及机毁人亡的风险要求是万无一失的,也就是可以接受的风险概率<0.0001。实际做不到的则另当别论。任务风险的概率既要考虑能接受的风险,又要参考可行性论证,即当前经过努力可以达到的水平而定;有时要在任务失败招致的后果损失,以及为减小风险概率而支付的代价之间进行权衡。当任务失败的后果损失小于为降低失效风险支付的代价,就可以接受这一失败风险概率,反之,应该支付相应的代价来降低任务失败的风险概率;也就是要提升需求的成功概率。但必须明确,上述任务失败的损失与降低失败风险支付的代价的权衡,不是就一次任务而论,而必须就全寿命周期进行全面的权衡。
在指标需求性论证的同时,随之进行指标可行性的初步论证,避免要求的指标完全脱离现实,无法在规定的时间内实现。实现指标的总体方案的可行性论证,则应由承制方负责进行。
4 可靠性、维修性、备件保障性的优化设计
在装备顶层参数指标可行性论证中,必然要涉及可靠性、维修性、备件保障参数单项指标的组合问题,也就是装备的失效率、维修率和备件保障概率如何分配的问题。
针对顶层指标来分配装备的失效率、维修率和备件保障概率,首先就避免了各自单独确定RMS单项指标的片面性和盲目性。在降低技术难度和寿命周期费用的目标下合理地进行RMS单项指标组合的参数优化设计。也就是说,在一定的范围内,当可靠度设计参数费用过高,可以用增强维修能力或增加备件数量来调节,使寿命周期总费用下降;或者当维修性要求难以实现,可以适当地提升可靠性水平以降低对维修性的要求;或者维修保障与备件保障参数之间相互调节,使总体的保障性设计易以实现等的权衡优化设计。
系统最终的优化设计,要求提供全系统的可靠性结构模型,以失效率、修复率、平均维修延误时间、平均备件延误时间参数表达的现场更换模块清单,用于证实可以满足系统顶层参数指标要求的全系统RMS设计。
5 虚拟数值的示例
装备RMS顶层参数指标的论证,是一个涉及总体方案、各项参数的预计和设计反复进行权衡的复杂过程,要全面阐述,篇幅不容。本文举一虚拟的示意性例子,用于简要说明RMS顶层参数指标论证的主要过程。
虚拟的示意性例子是论证确定机载火控雷达RMS顶层参数及其单项参数指标。
机载火控雷达的任务剖面是间断工作,描述机载火控雷达是以任务持续工作期内以任务成功或失效为准则,因此它的RMS顶层参数是任务成功率。假设在通常情况下,可以接受的最大风险为5%。这就是说,任务成功率应该≥0.95,并且这一概率在全寿命周期内通过维修保障和备件保障得以持续保持。火控雷达的单次任务持续工作时间ts=4 h,任务之间的间隔时间为2 h,即停机时间td=2 h。
由式(2)可知,任务成功率由两个部分组成:1)任务可靠度;2)战备完好率。首先假设机载火控雷达由6个分系统串联组成,它们的平均故障间隔时间分别为660、680、106、710、860、790 h。因此火控雷达的平均故障间隔时间为61.6 h,它的任务可靠度这一数值小于任务成功率。系统的薄弱环节在于第3分系统。进一步分析第3分系统,它由两部分组成,其平均故障间隔时间分别为920和120 h。设计方案对120 h部分采用并联冗余设计。由此系统的任务可靠度可以达到:

由式(2)可知,要求战备完好率POR大于等于:

要实现战备完好率,在系统失效率已经确定的情况下,就是对维修性要求和备件保障性要求进行权衡设计。
不难理解,维修性和备件保障性对系统现场更换模块数量的划分数量成相互反向的紧密关系。也就是说,划分现场更换模块量少,有利于维修性设计。不划分更换模块的整机作整体更换,故障不难发现,也无须定位,更换整机即告检修完成。但更换备件单元是整机,备件数量增加,备件费用激增;反之,更换模块划小,备件数量相对下降,但维修过程中的故障检测、故障定位难度大幅度增加,拆卸安装也相对复杂。
这就说明,系统存在最佳数量现场更换模块的划分,使技术难度降低和寿命周期中使用维修费用降低和备件配置费用降低的最优设计。由于模块划分与电路结构紧密关联,实际最优设计是不存在的,但相对优化设计完全可以做到。
由式(4)可知,火控雷达的平均备件延误时间和平均维修延误时间之和应该小于等于:

假设按照电路结构,火控雷达全机可以划分成32个更换模块,它们的失效率、修复率如表1所示。
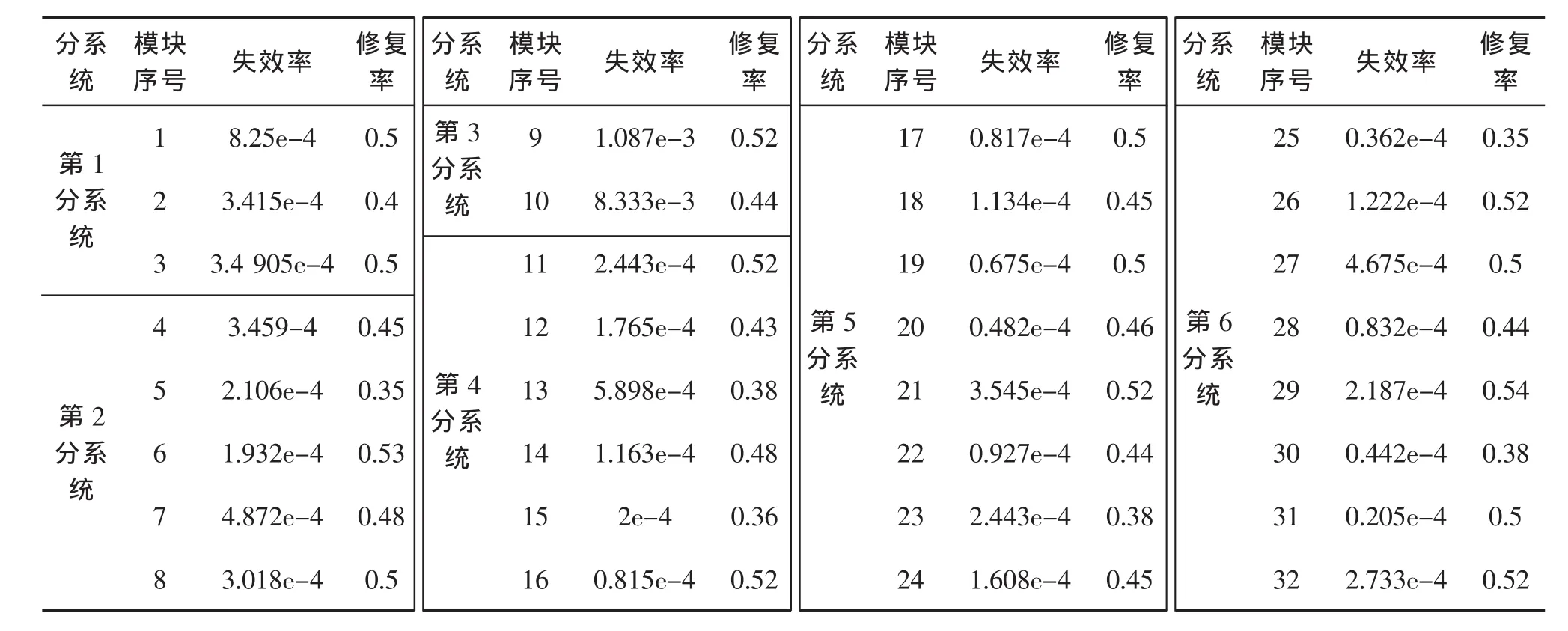
表1 火控雷达的失效率、修复率

式中:hi(ts)——第i序号模块的独立失效概率[5];
这说是说,仅从维修延误时间来说,已经大大超过了系统容许的延误时间。也说是说,即使现场备件充足,不存在备件延误时间,但维修延误为系统要求所不容。为此,必须大幅度提升各更换模块的修复率,而提升修复率的关键在于提高故障的检测、定位能力,从而必将增加机内检测设施的复杂性,这不仅要增加设施费用,且为机载重量、体积所不容。相反,火控雷达要求简化机内检测设施条件下提升故障检测定位能力。
出路在于合并现场更换模块,代价是增加机场更换模块的备件。
假设令第1、2、4分系统各合并为1个更换模块,第3分系统两个模块保持不变,第5分系统合并为两个模块,第6分系统合并为3个更换模块。合并后的现场模块更换单元如表2所示。
不难理解,模块合并后修复率容易得到提升的原因,在于把合并前复杂程度不同的多个模块不同失效模式的各自检测,转化为单一模块的失效检测。

这说明维修延误时间已经满足指标要求。
下面对备件保障进行优化设计。
由于上列10个更换模块均系可修模块,因此备件供应体制为两站点备件补充为实时方式的平均延误时间模型如下所示[6]:
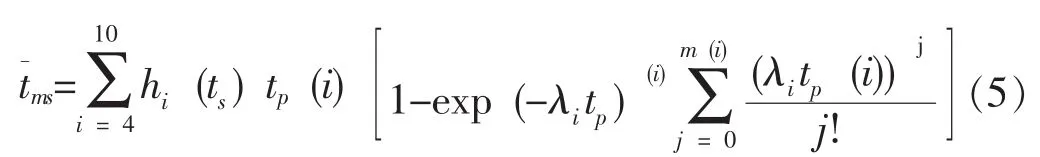

表3 模块现场最佳配置
由式(5)可以得到的平均备件延误时间等于0.0227839 h。由此可得战备完好率=0.982648>0.981593要求值。
实际上,就备件最佳设计,对于群体机载火控雷达来说,备件供应应该采用现场、库房、供应站三站点体制,可以进一步地减少备件数量,这在文献[5]、[7]中已经说过,此处从略。式(5)中:tp(i)——第i序号备件的周转时间,包括把故障部件送到检修站点运输时间、修复故障部件时间、回送部件到达现场的运输时间等;
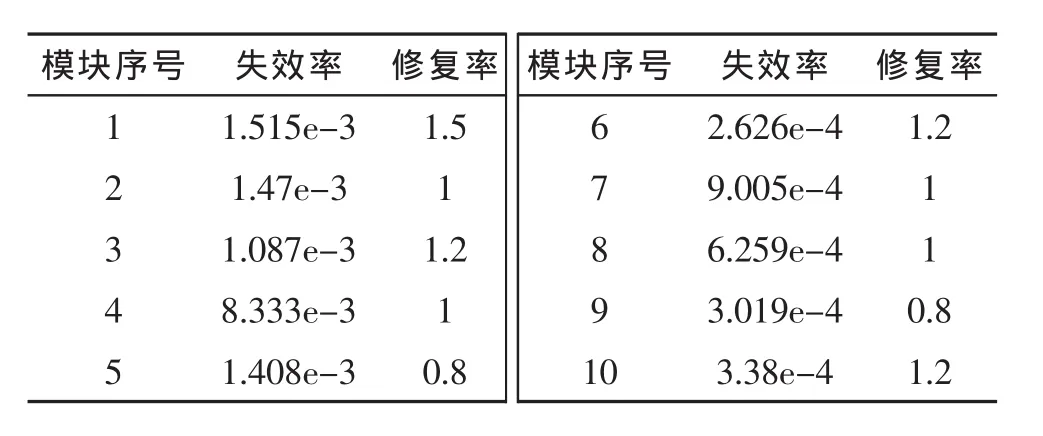
表2 合并现场模块更换单元
m(i)——换模块现场配置数量。
在上列模型基础上进行优化设计,得出模块现场最佳配置如表3所示。
为了减少篇幅,示例中的优化设计没有涉及费用问题。
实现上述10个现场更换的失效率、修复率和现场备件配置及其实时补充备件(即发生故障时,在现场备件更换故障部件后,故障部件立即送修复原后回送现场作为备件)的条件下(其中第4序号模型系双模块并联),保障了机载火控雷达在全寿命周期内每次4小时任务持续时间内达到≥95%的成功率。
6 结束语
RMS的顶层参数设计与由RMS的单项参数分别设计相比,其优越性是显而易见的。不仅可以定量地保障装备在全寿命周期内持续保持可靠工作的概率,而且可以通过可靠性、维修性和备件保障性参数的最佳组合,实现合理地降低寿命周期费用的优化设计的目标。
[1]丁定浩.确立任务成功率指标参数的目的和意义[C]//第十五届可靠性学术年会论文集.广州:中国电子学会可靠性分会,2010:1-4.
[2]丁定浩.能执行任务率模型[J].装备质量,2011,(5):1-4.
[3]丁定浩,陆军,王斌,新型战备完好率模型[J].电子产品可靠性与环境试验,2010,28(3):1-4.
[4]丁定浩,陆军.维修时间新参数和维修性设计新进展[J].中国电子科学研究院学报,2010,(4):381-384.
[5]丁定浩.以LRU的可靠性、维修性、备件保障性参数表达的战备完好率模型[J].装备质量,2011,(2):6-9.
[6]丁定浩.可修备件保障概率的适用模型[J].装备质量,2011,(8): 5-9.
[7]丁定浩.装备使用保障中寿命离散显著的备件保障研究[J].装备质量,2010,(11): 7-11。
