认知无线电中OFDM信号信噪比盲估计
2011-08-14刘明骞李兵兵唐宁洁李钊
刘明骞,李兵兵,唐宁洁,李钊
(西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)
1 引言
随着通信技术向无线、宽带方向发展,频谱资源日益紧张,认知无线电技术成为解决这一问题的关键技术之一[1]。正交频分复用(OFDM)技术不仅具有高的频谱利用率,而且满足了认知无线电对调制方式的要求[2],因此将大量用于认知无线电系统中。认知OFDM系统的关键技术之一是要解决次用户对OFDM信号的频谱感知和参数估计问题[3,4],其中信噪比为OFDM信号的重要参数之一。OFDM信号信噪比的估计方法可分为两类,一类方法是基于辅助数据的信噪比估计[5~7],另一类方法是无辅助数据的信噪比盲估计[8~11]。在认知OFDM系统中,无法从接收信号中提取导频、训练序列等辅助数据,因此OFDM信号的信噪比盲估计的方法值得进一步研究。
目前,OFDM信号信噪比盲估计的研究成果较少,文献[8]提出基于OFDM信号虚载波的信噪比估计,但该方法估计性能较差;文献[9~11]在多径信道下,根据OFDM信号的符号特性估计出信噪比,但均采用复杂度较高的多径信道阶数估计方法,使得整个信噪比盲估计方法的计算复杂度较大且估计精度较低;文献[12]采用重构信号的方法,根据接收信号的自相关函数与重构信号的自相关函数估计出信噪比,该方法复杂度高且不易于实现。
针对以上问题,本文提出一种低复杂度的OFDM信号信噪比盲估计的新方法,该方法首先利用循环前缀部分的自相关函数特性粗略估计出信道阶数,然后利用循环前缀中不受符号间干扰部分的自相关函数估计出信号功率,最后利用循环前缀是部分有用数据的复制这一特性,估计出噪声功率,从而估计出接收信号的信噪比。仿真结果表明,本文提出的OFDM信号信噪比盲估计方法在低信噪比多径信道下是有效可行的,且性能更优计算复杂度更低。
2 认知OFDM系统数学模型
对认知无线电条件下的信号接收,其前提是建立所认知对象的真实模型, OFDM已经应用于802 11a、802 16e、ADSL、DVB-T等标准。在分析这些标准的基础上,应建立认知OFDM系统发射机信号的数学模型。
设发送端发送的OFDM符号子载波个数为N,循环前缀长度为Nc,第m个OFDM符号的调制数据为Xm(k),k=0,1,…,N-1,则第m个OFDM发送符号可表示为
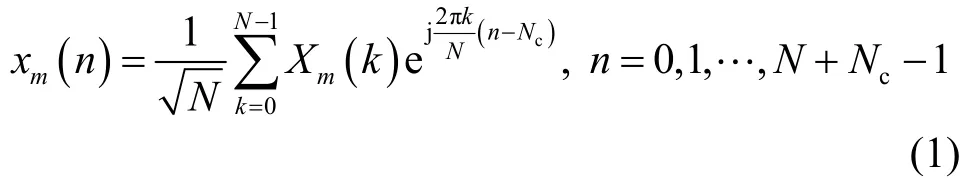
这里假设Xm(0),…,Xm(N-1)是独立同分布的随机变量。
信号通过的是多径信道,定义多径信道的冲击响应为h=[h0, h1,…,hl],其中,hl( l=0,1,…,L)为第l条路径的增益,L为信道阶数,其值等于多径信道的最大延时,为避免产生符号间干扰假设其值小于循环前缀长度Nc。若OFDM系统的符号定时及载波频偏均已同步[13,14],则经过多径信道后接收到的采样信号可以表示为
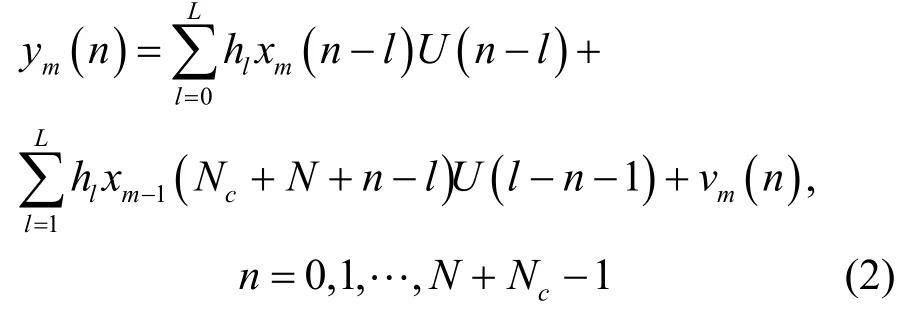
其中,U(·)为阶跃函数,vm(n)是均值为0,方差为的复加性高斯白噪声,且
3 OFDM信号信噪比的盲估计
3.1 信号功率的估计
图1描述了多径信道下,接收到的第m个OFDM符号的结构模型。由图1所示,将存在第m个OFDM符号数据的接收信号分成6个特殊的数据区间,其中,I1~I3表示数据区间中均存在第m个OFDM符号的循环前缀数据,I4~I6分别表示I1~I3中循环前缀数据所复制的有用数据部分。这6个特殊数据区间的范围可分别表示为

图1 多径信道条件下OFDM信号的结构模型
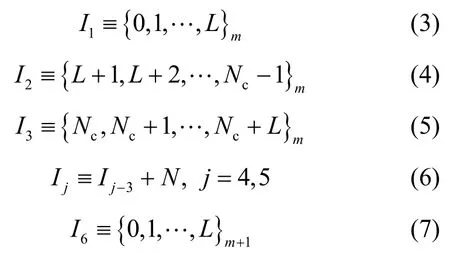
根据I1~I6的符号数据区间,定义3个不同的数据序列:
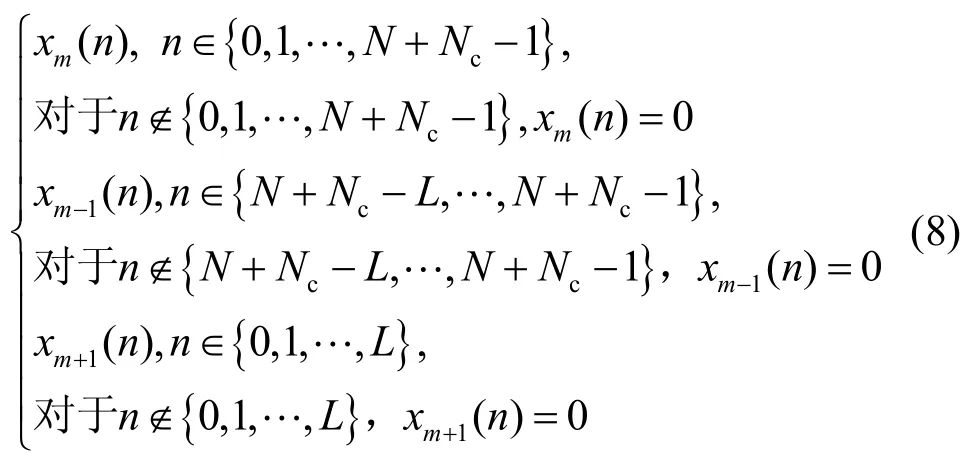
根据式(8)所定义的3个序列,得出I1~I6区间的数据yI1(n)~yI6(n)分别为
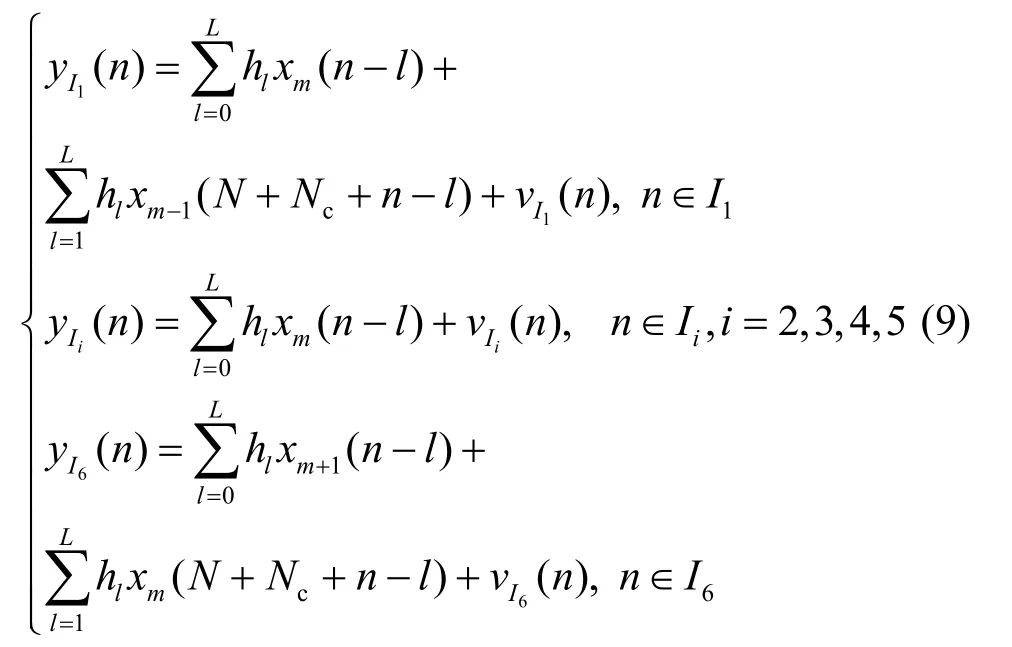
定义一个OFDM符号中关于每个采样点的自相关函数为
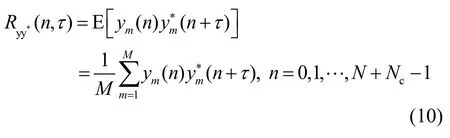
其中,M为接收端截取的OFDM符号数据个数,τ为相关延迟长度。由于循环前缀数据是部分有用数据的复制,容易得出当采样序列的采样点n∈I1∪I2∪I3,相关延迟长度等于N时,Ryy*(n, N)不等于0。当n分别属于I1,I2,I3时,n+N的采样点分别位于I4,I5,I6区间,由式(9)可推得Ryy*(n, N)(其中,n∈I1∪I2∪I3)的表达式为

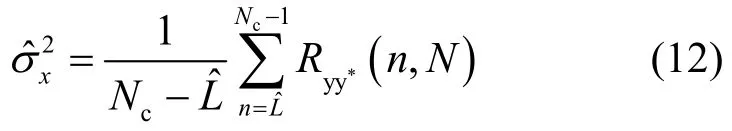
3.2 噪声功率的估计
OFDM符号中循环前缀数据为部分有用数据的复制,即:
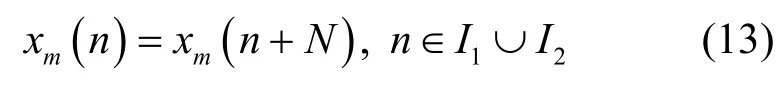
由式(9)可以看出,如果不考虑噪声的存在,则在不受符号间干扰的I2数据区间中,容易得出接收数据序列满足式(14):
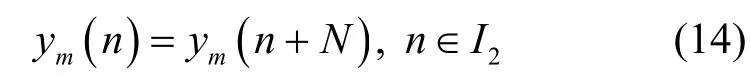
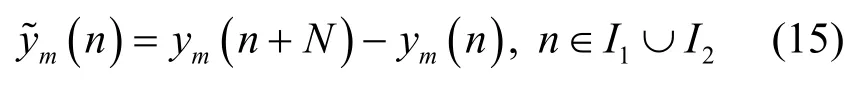
由式(9)、式(14)和式(15)可得:
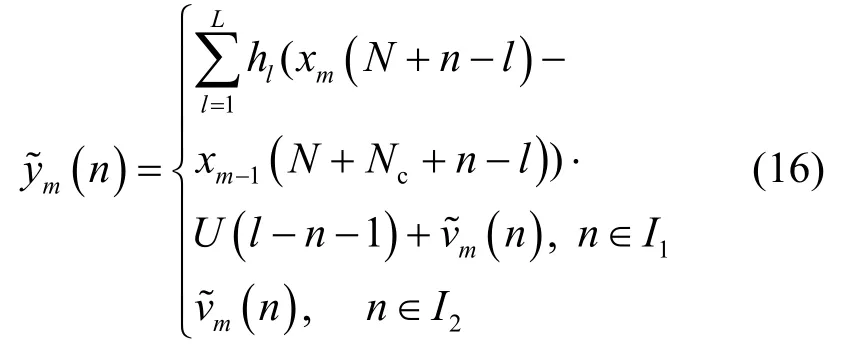
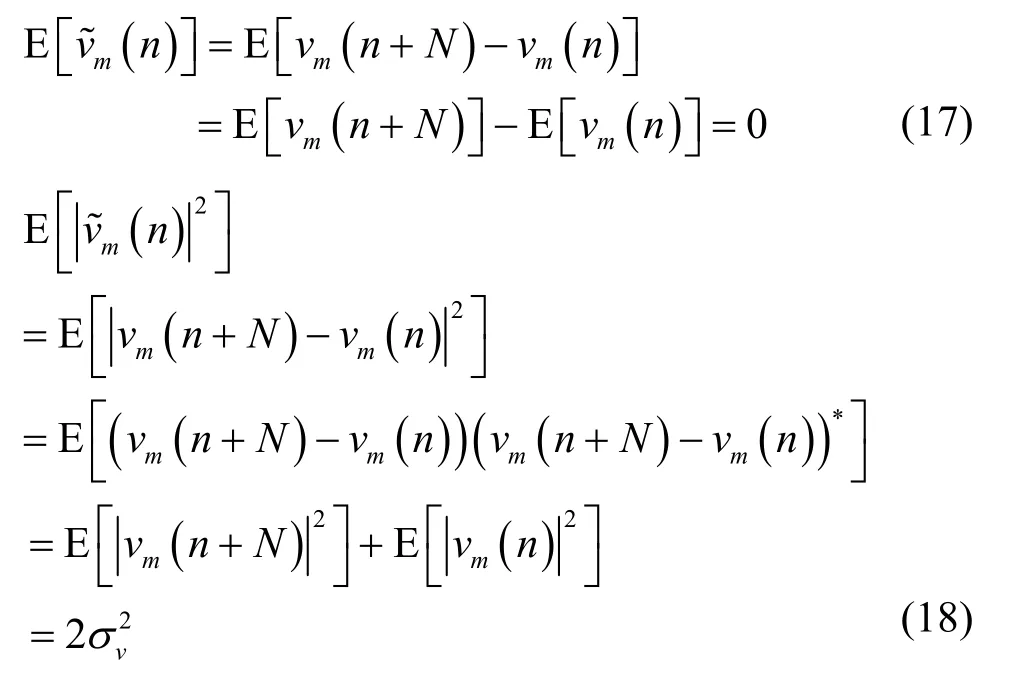
根据以上的分析,接收到的第m个OFDM符号中循环前缀部分的I1区间受到了符号间干扰的影响,而利用I2与I5区间的数据可以估计接收信号的噪声功率,由式(16)和式(18)可得噪声功率估计的表达式为
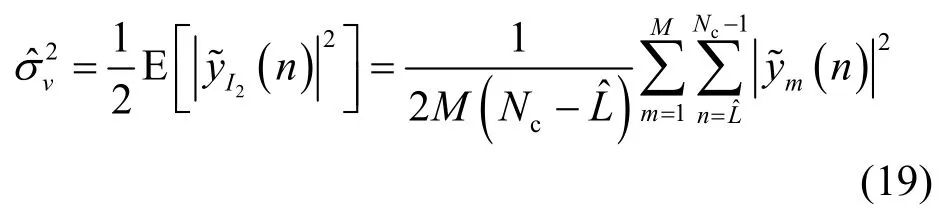

综上所述,如果估计接收端的信噪比,则需首先估计出多径信道阶数,以确定可利用的数据区间I2,因此多径信道阶数的估计是信噪比估计的必要环节。
3.3 多径信道阶数的粗估计
假设OFDM信号的时域参数已估计[15],在信道阶数L未知且接收端可以接收到足够多的符号个数时,可利用循环前缀中的最后一列数据进行信噪比估计,此时=Nc-1,利用式(12)和式(19)可得到理想的估计性能,并且大大降低了估计方法的计算复杂度。假如接收端可以接收到的符号个数较少,则需要估计信道阶数L,从而确定可利用的数据区间。文献[9]中利用MDL算法估计信道阶数L,其计算复杂度太高。本文根据接收的OFDM信号中循环前缀数据序列的自相关函数值的特性来粗略估计信道阶数L,如果估计值>L,即估计值在I2区间中,则可利用区间的采样点序列估计信噪比。
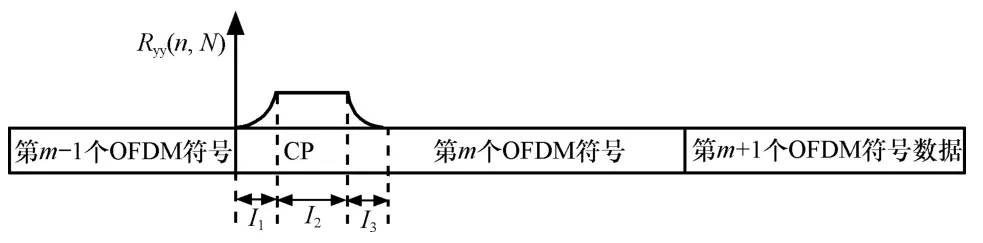
图2 自相关函数值特性
由式(11)得出,如暂时忽略循环前缀部分的符号间干扰,则自相关函数序列值有如图2所示的特性[16]。由图2可以看出,I2数据区间的自相关函数值是最大的且整个区间的值相同,因此通过检测自相关函数值的平坦区间即可估计得到数据区间,为了减小由于噪声干扰而引起的误差,定义平均自相关函数为
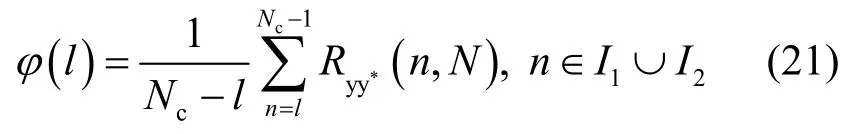
其中,l的取值区间为[0,Nc-1],易得上定义式与自相关函数值Ryy*(n, N)具有相同的特性,即在I1区间为递增特性,I2区间为平坦特性。因此可利用上定义式粗略估计信道阶数,确定数据区间,其具体估计过程为:检测φ(l)序列的值,以第一个满足φ(l +1)不大于φ(l)的l值作为信道阶数的粗略估计值。由于噪声及符号间干扰的影响,如果l的取值以1为步长,则容易提前终止检测搜索,因此定义一个步长λ,则序列φ(l)如式(22)所示,则估计的多径信道阶数为λl。
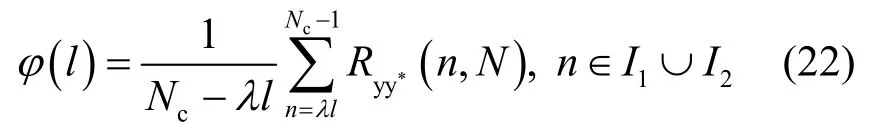
3.4 OFDM信号信噪比盲估计的步骤
综上所述,本文提出的认知 OFDM 系统中OFDM信号信噪比盲估计方法的具体步骤如下:
步骤1 根据已知的OFDM符号的总长度,如果接收端可以接收到足够多的符号个数,可利用循环前缀中的最后一列数据,此时= Nc- 1,则转至步骤5~步骤7估计出信噪比;如果接收端可以接收到的符号个数较少,则按照步骤2~步骤7估计出信噪比;
步骤2 根据已知的OFDM符号的循环前缀长度Nc及有效数据长度N,利用式(10)计算 I1∪I2区间数据的自相关函数 Ryy*(n , N);
步骤3 通过选择合适的步长λ的大小,利用式(22)计算平均自相关函数 φ ( l );
步骤4 检测 φ ( l )序列中第一个满足φ (l +1)不大于 φ (l)的l值,估计出多径信道阶数λl;
4 仿真结果及性能分析
为了验证本文方法的有效性,通过MATLAB仿真软件进行仿真实验,其所使用的仿真条件为:信号子载波个数为 256,循环前缀长度为 64;采用的多径信道模型为 9径信道,每条信道的增益系数满足l =0,1,… ,8 ;蒙特卡洛仿真次数为500次。本文所采用的性能评价指标为估计偏差Gbias及估计均方误差Gvari,分别定义为
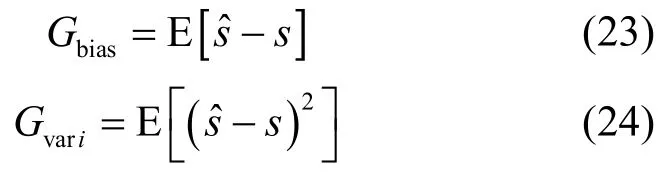
步长的选取影响信道阶数的估计,从而影响OFDM信号信噪比的估计性能,图3描述了不同的步长大小对本文信噪比估计性能的影响。从图3可以看出,在低信噪比时,步长的大小对估计性能的影响不大,而高信噪比时受步长的影响较大。原因在于低信噪比时,符号间干扰值较小,因而所引入的误差也较小;在高信噪比时,只有当信道阶数的估计值大于真实的信道阶数时,才能得到较准确的信噪比估计值,当步长较小时,设定的φ ( l )的截止搜索条件容易提前结束,进而引入符号间干扰,而当步长较大时,可保证信道阶数的估计值在数据区间。因此,所选用的步长大小与仿真参数中循环长度的大小有关,本文仿真试验中循环长度设为64,根据图3可以看出当步长为5时,本文信噪比的估计性能最佳。

图3 不同步长对本文估计性能的影响
图4是已知信道阶数和未知信道阶数下的估计性能对比,其中未知信道阶数时,分2种情况:一种是基于循环前缀最后一列数据的信噪比估计,另外一种是基于信道阶数粗估计的信噪比估计,并采用估计偏差量作为性能评价标准。从图4中可以看出:1)截取的符号数为100时,基于信道阶数粗估计的信噪比估计的性能接近于已知信道阶数情况下的估计性能;由于截取的符号个数较少,基于循环前缀最后一列数据的信噪比估计的估计性能较差;2)截取的符号个数为500时,基于循环前缀最后一列数据的信噪比估计的估计性能在-10dB条件下,估计偏差不大于0.1dB,并且省略信道阶数估计过程,降低了计算复杂度。由以上分析可得,在可截取的OFDM 符号个数较多时,可以无需进行信道阶数估计,直接利用循环前缀中最后一列数据进行信噪比估计;如果截取的OFDM符号个数较少时,利用本文的信道阶数估计方法,仍然可得到良好的信噪比估计性能。
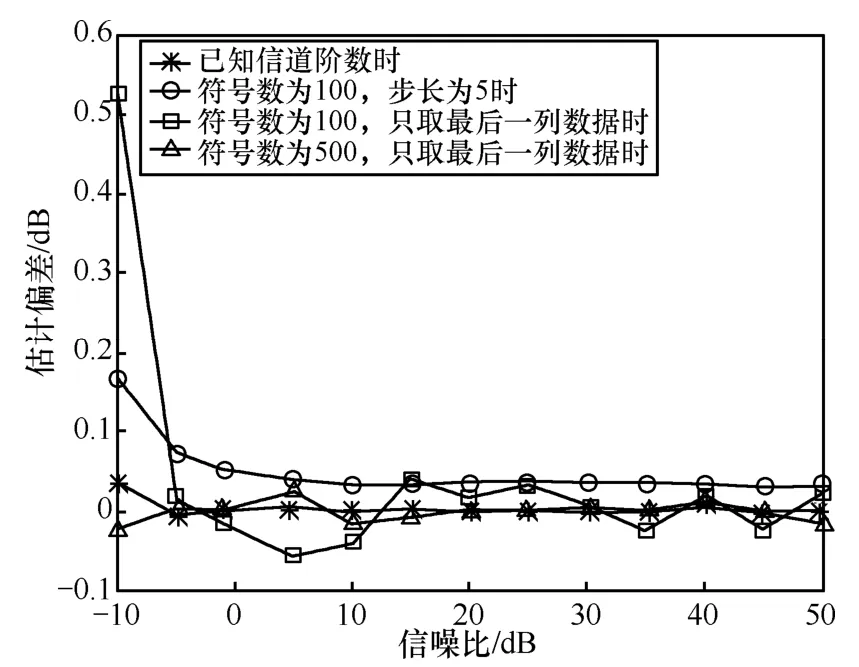
图4 不同条件下的估计性能对比
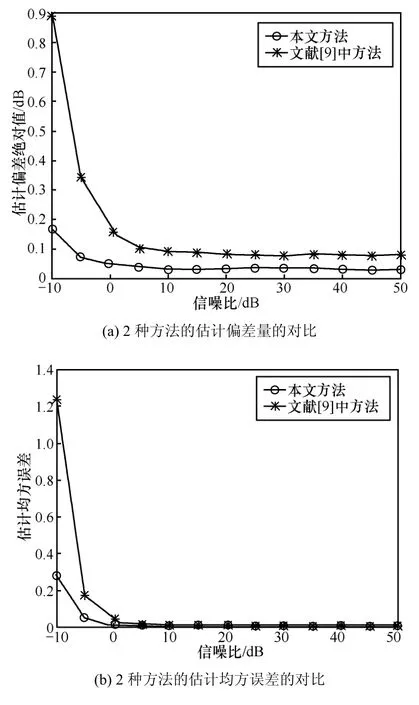
图5 2种估计方法的估计性能对比
图5描述了本文信噪比估计方法与文献[9]中估计方法在相同仿真条件下的性能对比,图 5(a)为 2种估计方法的估计偏差量的对比,图5(b)为2种估计方法的估计均方误差的对比。从图5中可以看出,本文的信噪比估计方法在估计性能上优于文献[9]中的估计方法。由本文第3节的理论分析可以看出,本文方法与文献[9]一样,计算复杂度主要在于信道阶数的估计,即式(10)和式(22)的计算。如果只考虑乘法运算所带来的计算复杂度,则易得本文方法总的计算量为MNc,而文献[9]中采用MDL算法估计信道阶数,其总的计算量为,从而可以看出本文信噪比估计方法的计算复杂度远低于文献[9]中估计方法的计算复杂度。因此本文提出的方法不仅估计性能好且计算复杂度低,更适合于认知OFDM系统中OFDM信号的信噪比盲估计。本文方法主要取决于多径信道最大延时的粗估计,而本文提出多径信道最大延时粗估计方法不仅适用于仿真实验中的 OFDM 信号,对于其他标准(如DVB-T、802.16e等标准)中的OFDM信号同样也适用。因此,本文提出的OFDM信号信噪比盲估计方法具有普遍适用性。
5 结束语
针对认知OFDM系统中传统的OFDM信号信噪比盲估计方法的估计精度低且计算复杂度高的问题,本文提出一种低复杂度的盲估计新方法。该方法首先利用循环前缀中自相关函数的特性粗略估计多径信道阶数,然后利用无符号间干扰区域数据的自相关函数值估计信号功率,并利用循环前缀数据为部分有用数据的复制这一特性估计噪声功率,从而估计出接收信号的信噪比。仿真结果表明,本文方法在低信噪比多径信道下的估计性能优于传统方法的估计性能,且计算复杂度更低。
[1] MITOLA J, MAGUIRE G Q. Cognitive radio: making software radios more personal [J]. IEEE Personal Communications, 1999, 6(4): 13-18
[2] MAHMOUD H, YUCEK T, ARSLAN H. OFDM for cognitive radio:merits and challenges[J]. IEEE Trans Wireless Commun, 2009, 16(2): 6-15.
[3] 虞贵财, 罗涛, 黄振等.感知无线电系统中改进的循环频谱检测算法[J].北京邮电大学学报, 2009,32(2): 89-92.YU G C, LUO T, HUANG Z, et al. An improved cyclic spectrum detection algorithm in CR systems [J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(2): 89-92.
[4] 蒋清平, 杨士中, 张天骐. 认知无线电中 OFDM 信号联合参数估计[J]. 北京邮电大学学报, 2011, 34(2): 132-135.JIANG Q P, YANG S Z, ZHANG T Q. Joint parameters estimation of ofdm signals in cognitive radio[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(2): 132-135.
[5] LI J G, TANG W B, LI S Q, et al. A simple and effective snr estimation algorithm for OFDM in rayleigh fading channels[A]. 7th Interna-tional Conference on Information, Communications & Signal Processing[C]. Macau, China, 2010.172-176.
[6] MILAN Z, RUDOLF M. An improved preamble-based SNR estimation algorithm for OFDM systems[A]. 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications[C]. Instanbul, Turkey, 2010. 172-176.
[7] RANA S M, WABO M, VARUN J, et al. Front-end estimation of noise power and SNR in OFDM systems[A]. International Conference on Intelligent and Advanced Systems[C]. Kuala Lumpur, Malaysia, 2007.435-439.
[8] 任光亮, 张辉, 常义林. 基于虚载波的OFDM系统信噪比盲估计方法[J]. 西安电子科技大学学报,2004 ,31 (2): 186-189.REN G L, ZHANG H, CHANG Y L. An SNR blind estimation technique based on virtual carriers in OFDM sytems[J].Journal of Xidian University, 2004 ,31 (2): 186-189.
[9] WANG K, ZHANG X D. Blind noise variance and SNR estimation for OFDM systems based on information theoretic criteria[J]. Signal Processing, 2010,90(9): 2766-2772.
[10] CUI T, TELLAMBURA C. Power delay profile and noise variance estimation for OFDM[J]. IEEE Communication Letters, 2006, 10(1):25-27.
[11] SOCHELEAU F X, ABDELDIALIL A B, SEBASTIEN H. Non data-aided SNR estimation of OFDM signals[J]. IEEE Communication Letters, 2008, 12(11): 813-815.
[12] KIM S, AN D, RYU H, et al. Efficient SNR estimation in OFDM system[A]. Proceedings of 2011 IEEE Radio and Wireless Symposium[C]. Phoenix, AZ, USA, 2011. 182-185.
[13] CHEN J, LI M, KUO Y H. Adaptive OFDM synchronization algorithm in frequency selective fading channels[J]. IEEE Transactions on Consumer Electronics, 2009, 55(4): 1841-1846.
[14] SHA Y, LI M M, CHU J F. A novel timing and frequency synchronization technology for OFDM system[J]. Journal of Networks, 2011, 6(4):646-653.
[15] PUNCHIHEWA A, BHARGACA V K. Blind estimation of OFDM parameters in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(3): 733-738.
[16] CHIN W L. ML estimation of timing and frequency offsets using distinctive correlation characteristics of OFDM signals over dispersive fading channels[J]. IEEE Transactions on Vehicular Technology, 2011,60(2): 444-456.
