基于自适应方向性滤波和非局部均值修补的CT图像金属伪影消除

李印生 陈 阳 马建华 罗立民 陈武凡

1(东南大学计算机科学与工程学院，南京 210096)

2(南方医科大学生物医学工程学院，广州 510515)

引言

CT系统中，许多因素可以在重建结果中产生伪影，在这些伪影中，金属伪影最为明显。CT扫描中，金属等高衰减系数的物质导致到达探测器的光子计数十分稀少，读取的投影值就异常大，使得对于断层结构的判断带来很大困难。这些金属物体包括外科手术中的金属夹子、金属修补物、填充物和金属假牙等。由于这些高衰减系数的物质大多都是各种金属，所以由这些物体引起的伪影统称为“金属伪影”。

金属伪影消除算法较多，可以大致分为三类：投影插值法、迭代法和混合方法。投影插值法理论简单，实现快速，但对于全局放射状伪影效果欠佳。迭代法能够有效处理复杂的伪影问题，但由于计算量过大而限制其使用。混合法结合两者优点，目前受到广泛关注。

近年来，基于投影(弦图)空间插值算法形成了前置滤波、分割和投影插值的较为统一的框架[2]。前置滤波可以在一定程度上降噪并对于条状伪影进行平滑处理。分割则是十分关键的一步，目的在于将图像中的金属成分和伪影成分与其他组织进行区分，继而进行提取。分别对原始图像和金属成分进行前向投影，得到相应的弦空间数据。做差运算即可将金属伪影成分从弦空间中去除。然而，将金属弦图从原始图像正弦图中减除后，会造成原有的肌肉、软组织等投影的不连续现象，反投影后，会产生新的伪影[2]。因此，需要对于投影空间数据进行插值处理。例如，2006年Matthieu等提出的金属伪影消除算法就是采用了上述流程，取得一定的效果[2]。但是，Matthieu的算法有两点明显的不足：一是k-means聚类分割需要人工指定聚类数和聚类中心，两者的设置随图像的不同需要做出调整，不具一般性;同时，聚类数的设置会影响到算法运行的效率和效果[4]。二是 Radon空间补全采用线性插值算法，利用局部信息补全弦图中减除的部分。显然，Radon空间补全还可以通过基于全局修补的方法以达到更好的结果。

本研究同样采用上述算法框架，针对 Matthieu算法的不足，提出了基于方向性自适应前置滤波，配合均值漂移(Mean shift)和最大互信息熵(MMS)分割[4]，最后使用非局部均值图像修补(nonlocal means inpainting)[5]的新的金属伪影消除算法。采用体模仿真图像和真实CT图像进行实验，结果表明，所提出的算法能有效地去除CT图像中的金属伪影。

1 方法

1.1 自适应方向性高斯滤波器

采用方向性自适应滤波器(adaptive steering filter，ASF)，该滤波器具有滤波方向，尺度随图像局部几何结构而改变，并且滤波强度人工可调;能够很好的完成CT金属伪影去除流程中前置滤波器的功能[2]。对于选取的各项异性高斯核阐述如下：

设G0为配分常数，σ1、σ2为各项异性高斯核的尺度系数，见图1。各项异性高斯卷积核表述为

图1 高斯卷积核平面投影Fig.1 The Gauss convolution kernel

式中，d1=u cosθ+v sinθ d2=u cosθ-v sinθ

其后，由非线性各向异性结构张量(nonlinear anisotropic structure tensor，NAST)对图像局部结构进行估计，继而确定ASF的尺度系数σ1、σ2和旋转角度θ。结构张量(以下简称 ST)通过求解图像局部的梯度信息，构造张量矩阵，根据其特征值和特征向量的具体形式判断图像的局部几何结构[8]。

首先定义图像f的张量积矩阵

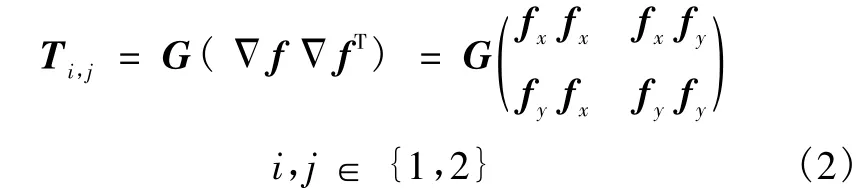
式中，fx、fy分别表示图像对 x、y方向的一阶偏导数。使用滤波算子 G(·)对张量矩阵进行滤波处理，当G(·)为线性运算时，称为线性结构张量，当G(·)为非线性运算时，称为非线性结构张量。线性结构张量一般由式(2)中的张量矩阵与高斯核函数卷积得来，不可避免地造成图像平滑模糊[8]。故采用非线性各向异性结构张量估计图像局部结构，定义为

ε为补偿系数，为了保证根号下的值为正数。p为边缘强度，取 p=1.5进行实验。最后，将 ∂tTi，j对于扩散时间t进行积分，即可求得经非线性扩散滤波处理后的NAST矩阵。

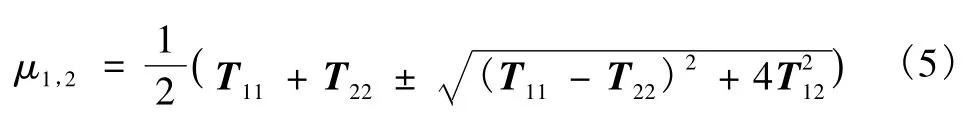
NSAT 矩阵特征值[8]与矩阵特征值对应的特征向量可以反映图像的局部结构，例如，对于图像均质区域，灰度值变化程度比较平缓，张量矩阵的特征值较小或为0。对于图像边缘、角点或是被条状伪影污染的部分，特征值较大[8]。此处ASF的作用就是要检测出条状伪影辐射的方向，并提供合适的卷积强度平滑条状伪影。

根据以上阐述，首先确定伪影强度。ASF滤波器示意见图2。对于 ASF的长轴尺度，采用文献[2]中的方法进行估计。设 σ1是条状伪影参考坐标系中与伪影正交方向的ASF滤波尺度，同样，对于ASF的滤波方向，采用文献[8]中的方法进行估计。式(1)中的G0为配分常数，使得

即可确定G0取值。

图2 ASF滤波器示意Fig.2 ASF filter

最后，采用 ASF对图像进行前置滤波。假设I0(x，y)为待处理图像中某处灰度值，IASF(x，y)是经过ASF处理后的同一位置处的图像灰度值，Gx，y(u，v)为 ASF滤波核函数，则前置滤波过程可表述为

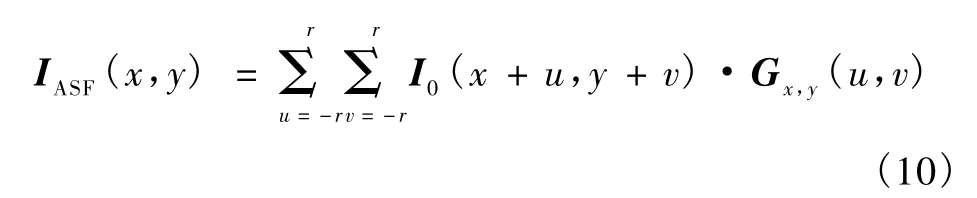
取r=2作为卷积核掩模的半径。

1.2 最大互信息熵结合均值漂移的图像金属及伪影成分的分割

金属及其伪影成分的精确分割是影响CT金属伪影去除结果的重要因素。为了有效的分割出图像中包含的金属和条状伪影，采用均值漂移结合最大互信息熵方法分割图像中的金属成分及其形成的条状伪影。

最大互信息熵是针对k-均值聚类算法和Meanshift图像分割算法这类区域生成算法的不足之处而专门设计的[4]。它基于模拟退火(Simulated Annealing)过程，以最大互信息量(MI)作为优化分割目标，以互信息熵差(d MI)作为分类数判据的一种优化阈值分割算法。当其小于某一阈值时，认为分割结束。以原始图像和当前分类数下的分割图像的互信息量为优化目标。当互信息熵差达到最小值，同时互信息量达到最大值时，认为达到最优分割[4]。可见，该分割方法是典型的多聚类数分割，可以将金属和条状伪影及其他组织成分有效的区分。对于体模图像和临床真实图像，选取的最大聚类数分别取为5和16。算法原理和实现过程具体参见文献[4]。

1.3 结合线性插值的非局部均值Radon空间修补

在经过前置滤波和分割去除伪影后，如果不对分割后的弦空间数据进行有效的修复，则做差运算后，代替原来金属成分的部分与其周围组织在弦空间的融合处不连续，重建后会产生新的伪影[2]。为了有效去除伪影，并最大限度地保证周围其他组织不被破坏，本研究采用非局部均值修复的方法进行Radon空间的补全。基于较大遍历窗的非局部均值修补，能够有效利用图像全局信息。图像修复模型的算法原理为

Nonlocal权重系数为

Ni、Nj为以 i、j为中心，Rsim为半径的一个小邻域，h为衰减强度。

加权滤波定义为

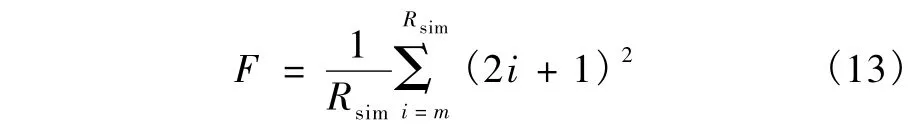
Z归一化常数定义为

联立式(11)～(14)，得到用于图像恢复的 Nonlocal加权项，完成图像修补。

为了清楚阐述修补过程，定义以待修补区域像素为中心的邻域为目标窗。当前计算权重的像素邻域为相似窗。非局部均值修补的具体步骤如下：

首先以分割出金属以及伪影成分弦图数据定义掩模，将待修补图像相应位置用掩模覆盖;继而提取掩模部分(待修补区域)的边界，并设置目标窗、相似窗半径Rsim，沿边界顺时针并逐步趋向待修补区域中心进行遍历搜索;对于算法本身设置权重阈值δ和合适的衰减常数h;若当前求得的相似权重w(i，j)≥δ，则将相似窗数据复制给目标窗，否则，采用线性插值方法直接由目标窗邻近数据进行局部修补。

做出这样的改进，是出于实际情况考虑的。首先，作者通过实验发现，在有些情况下，无论如何设置窗口半径Rsim和衰减常数h都可能无法找到与目标窗相似程度较高的相似窗，这样的修补无疑会产生较大误差。此时应采用线性插值由目标窗附近的数据直接进行插值修补。并且，由待修补区域边缘顺时针向内的修补也符合常用的图像修补原则。实验证明，这种方法是可行的。最后，只需将修补处理后的弦空间数据进行FBP重建，可得到本算法处理后的结果。

算法步骤为

步骤1：采用ASF前置滤波器对含有金属伪影的图像进行全局滤波;

步骤2：分别采用均值漂移分割滤波后图像的金属成分，采用最大互信息熵分割滤波后图像的伪影成分;

步骤3：分别对包含伪影成分的图像和原始图像进行前向投影;

步骤4：在原图投影中，依据金属和伪影成分投影制作掩模;

步骤5：采用非局部均值结合线性插值方法对弦空间进行修补;

步骤6：采用FBP方法得到修补后弦空间数据的空间域图像;

步骤7：将步骤6得到的图像和均值漂移分割出的金属成分进行空间域插值，得到最后的校正图像。

1.4 算法验证实验

实验分别采用体模和真实临床数据，对本算法进行验证和比较。CT图像维数采用512像素×512像素。重建图像采用 FBP算法，其中滤波核采用“B40 f”。校正算法中采用平行束成像几何。图3(a)是一个包含金属伪影的模拟CT图像，它包含了一个金属植入物和一个圆柱形水容器。标准体模图像基于下面的 CT值设置：空气，0;方形水槽，500;圆柱形水槽，3000;水，1000。图 3(b)是病人肝脏金属缝合物产生的条状伪影。计算机硬件环境为Inter Core i52.68×4 GHz，6 GB RAM。为了缩短校正时间，本研究采用混合Matlab/C++编程环境。

图3 采用的带有金属伪影的体模与真实临床CT图像。(a)带有金属伪影的体模CT图像;(b)带有金属伪影的临床CT图像Fig.3 The original images.(a)phantom image;(b)clinical CT image

非均值修补算法能有效利用图像冗余信息，由于要遍历整幅图像，因此算法效率不高。其滤波效果对遍历路径、窗口半径大小、衰减常数和判别阈值δ(见1.3中步骤4)十分敏感。笔者进行大量实验，最终采用Rsim=5，h=2.5对仿真体模图像进行修补，采用Rsim=3，h=1.2对临床图像进行修补。但实验中由于相似程度过低，而使用线性插值的情况也有出现(见1.3中步骤4)。判断标准为：每次固定目标窗，遍历所有相似窗而求得的最大权重wmax，当wmax≥δ=0.3时采用非局部均值修补，否则采用双线性插值修补。

2 结果

分别采用本算法和文献[2]中算法校正结果如图4所示。其中的ASF滤波强度主要由此函数中的滤波掩模大小、NAST中的高斯卷积核平滑强度(滤波尺度)决定。使用较大的掩模，滤波强度大，计算较慢。高斯核的平滑尺度越大，平滑效果越好。图4中(a)和(c)采用文献[2]中算法，作为对比。图4中(b)和(d)选用掩模半径为3，平滑尺度为1.5的ASF滤波。高强度ASF滤波可以有效去除条状伪影，但过大的强度使得复杂的临床图像中被伪影污染的肌肉、软组织等一律被滤除，因此必须确定合适的滤波强度。所有结果图像与原始待处理的图像采用相同的窗宽。

从图4中(a)和(c)对于临床图像的校正可以看出，文献[2]中算法可以在一定程度上滤除条状伪影，但金属边缘处仍有残余。对比之下，本校正算法可以在有效消除条状伪影前提下，最大限度使原有的图像不被破坏，从而保证校正后的图像仍具有临床价值。对比图4(a)、(b)，对于水的重建，本算法结果(图4(b))匀质区域的一致性更高。对比图4(c)、(d)，对于重建图像中的条状伪影的抑制更好。

图4 分别采用文献[2]和本算法对体模、临床图像的伪影消除后的结果。文献[2]算法用于体模图像;(b)本算法对用于体模图像;(c)文献[2]算法用于临床图像;(d)本算法对用于临床图像Fig.4 The corrected phantom and clinical CT image using the algorithm in Ref[2]and our proposed algorithm.(a) the corrected phantom using the algorithm in Ref[2];(b)the corrected phantom using our proposed algorithm;(c) the corrected clinical image using the algorithm in Ref[2];(d) the corrected clinical image using our proposed algorithm

3 讨论和结论

所提出的算法也存在不足。如何有效区分图像边缘和条状伪影是本算法亟待解决的问题。另外，非局部均值修补算法虽然可以有效利用图像的全局信息，但算法效率不高(相比插值等方法)。进一步的工作希望构造修补误差泛函，通过求解其极值寻找最佳的窗口大小和衰减常数，使得非局部均值修补达到更好的效果。

CT图像金属伪影的消除是一个重要课题。本研究采用自适应方向性前置滤波器对含有伪影的图像进行处理，在一定程度上抑制条状伪影。其后采用均值漂移分割出图像中的金属成分。最大互信息熵分割算法能够较为有效地提取金属物周围伪影。在获取原始图像和金属成分的弦空间数据后，本算法采用非局部均值结合线性插值方法对弦空间图像进行修补。当相似性低于给定阈值时，直接采用线性插值方法由待修补区域周围数据对其进行修补。实验表明，这样的结合有助于减少弦空间修补时的误差，最后采用滤波反投影得到校正后的图像。

[1]Manzke R， Grass M， Hawkes D. Artifact analysis and reconstruction improvement in helical cardiac cone beam CT[J].IEEE Trans on Medical Imaging，2004，23(9)： 1150-1164.

[2]Matthieu B and Lothar S.Metal artifact reduction in CT using tissue-class modeling and adaptive prefiltering[J].Medical Physics，2006，33(8)：2852-2859.

[3]Ullrich K.The edge and junction detection with an improved structure tensor[J].Pattern Recognition，2003，36(2)：25-32.

[4]Lu Qingwen，Chen Wufan.Image segmentation based on mutual information[J].Chinese Journal of Computers.2006，29(2)：296-301.

[5]Wong A，Orchard J.A nonlocal means approach to exemplarbased inpainting[J].ICIP，2008，14(3)： 2600-2603.

[6]Buades A，Coll B，Morel JM.A review of image denoising algorithms，with a new one[J].Multiscale Modeling and Simulation，2005，4(2)：490-530.

[7]Buades A.Image and film denoising by non-local means[D].Illes Balears： University of Les Illes Balears，2006.

[8]Wang Wei， Gao Jinghuai， Li Kang. Structure-adaptive anisotropic filter with local structure tensors[C]//IEEE Computer Society. Second International Symposium on Intelligent Technology Application： Shanghai： IEEE，2008：1005-1010.

[9]Brox T，Weickert J，Burgeth B，et al.Nonlinear structure tensors[J].Image and Vision Computing.2006，24：41-55.