基于自回归模型和关联向量机的癫痫脑电信号自动分类

韩 敏 孙磊磊 洪晓军 韩 杰

1(大连理工大学电子信息与电气工程学部，大连 116023)

2(大连医科大学附属第一医院，大连 116011)

引言

癫痫是一种常见神经系统疾病，在全世界范围内大约有1%的人饱受其困扰，脑电图检查是一种常用的辅助诊断方法。由于癫痫发作的突然性，传统的脑电图采集方法很难记录到癫痫病人发作期的脑电信号。近年来，随着计算机技术的发展，长程视频脑电图机得到了广泛应用。长程视频脑电图的记录时间可以从数小时到数周，因而能够很好地记录癫痫病人发作间期、发作前期和发作期的脑电信号，为癫痫的诊断带来了极大的便利。长程视频脑电图在采集大量脑电数据的同时，也给医生带来了巨大的工作负担。人工阅读这些脑电图既费时又费力，因此脑电信号的自动检测和分类渐渐成为研究者的共识。尤其是机器学习方法，近年来广泛应用于脑电信号的自动检测和分类，并取得了较高的分类精度[1-12]。

采用机器学习方法实现癫痫脑电信号的自动分类，首先需要对脑电信号进行特征提取。基于波形特征的脑电信号特征提取方法在癫痫脑电信号分类的早期研究中比较常用，可以被看成是人眼观察法的延伸，正如人眼能够观察到的信息总是有限的，很多有价值的信息在这类脑电信号特征中得不到体现。随着脑电信号的非线性确定性渐渐为人们所接受，非线性动力学方法也成为一类主要的脑电信号特征提取方法。但是，脑电信号的非线性特征提取方法通常计算过程比较复杂，计算时间比较长，并且其分类性能与线性特征提取方法相比没有明显优势[13]。基于自回归模型的脑电信号特征提取是一种线性特征提取方法，自回归模型系数可以很好地反映大脑的生理功能和思维状态，在癫痫脑电信号分类研究中得到了广泛的应用[1-5]，因此采用自回归模型进行脑电信号的特征提取。目前，几乎所有的癫痫脑电信号分类方法都是将特征提取得到的脑电信号特征直接输入分类器[1-12]，而无论是 Ubely 等的研究[4]，还是笔者之前的研究[5]，都表明自回归模型系数可以很好地区分癫痫脑电信号，甚至单个特征的分类准确率可以达到90%以上。这意味着可以通过引入特征变换方法对特征空间降维，在保证较高分类精度的同时，降低模型复杂度，提高算法计算效率。本研究首次将特征变换引入癫痫脑电信号分类，分别采用主成分分析和线性判别分析两种特征变换方法，降低特征空间维数。

在癫痫脑电信号分类研究中，人工神经网络是最常用的一类分类器。目前，已经用于癫痫脑电信号分类的人工神经网络有：多层感知机[1]、递归神经网络[6]、径向基函数网络[7]、支持向量机[3-4，8-9]，等等。其中，支持向量机可以很好地处理高维小样本问题，泛化性能良好，模型比较稀疏，因而在脑电信号分类研究中得到了广泛的应用。尽管如此，支持向量机也存在着一系列缺点：正则化系数需要通过交叉验证确定，核函数需要满足Mercer条件，不能得到概率式输出[14]。近年来提出的关联向量机基于贝叶斯学习框架，可以有效克服支持向量机的上述不足，并且得到的模型更为稀疏[14-15]，使得在脑电信号分析中测试速度更快，脑电信号分析的实时性更强，概率式输出则更有助于医生的诊断决策。因此，本研究选用关联向量机作为分类器。

1 相关原理介绍

1.1 基于自回归模型的脑电信号特征提取

脑电信号特征提取，即从脑电信号中提取有价值的信息，并以此作为分类器的输入;基于自回归(autoregressive，AR)模型的脑电信号特征提取，即将AR模型系数作为脑电信号的分类标准。根据Box和 Jekins的描述[16]，p阶 AR 模型 AR(p)可以表示为

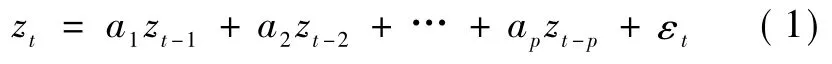
式中，zt为时间序列t时刻观测值，ai为 AR模型系数，εt表示白噪声。

在AR模型系数的求解过程中，首先需要确定AR模型的阶次p。通常AR模型阶次由AIC信息准则确定，AIC表示为

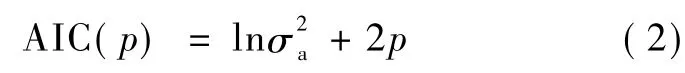
当时间序列包含n个观测值时，式(2)中σa定义为

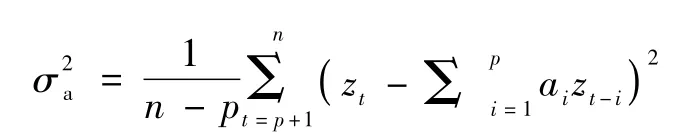
AIC取得最小值时，对应的p值为模型的最优p值。除确定AR模型阶次外，还需对参数估计方法进行选择。AR模型系数常见估计方法有：最小二乘法、解Yule-Walker方程法、Burg法，等等。其中，Burg法可以直接从时间序列得到AR模型系数，计算效率比较高，即使时间序列包含的观测点比较少，也可有效地估计AR模型系数。因此，本研究选用Burg法估计AR模型系数。

1.2 特征变换

目前，几乎所有的癫痫脑电信号分类方法都是将提取得到的脑电特征直接输入到分类器[1-12]。实际上，并不是所有的特征对最终的分类精度都有贡献，并且特征之间很可能存在着大量的冗余。特征变换方法将提取得到的脑电特征重新组合，并从中选择几个主要特征作为分类器的输入，可以有效降低输入空间维数，降低模型复杂度，提高模型计算效率。

本研究采用两种经典的线性特征变换方法：主成分分析(principle components analysis，PCA)和线性判别分析(linear discriminant analysis，LDA)，对提取得到的脑电信号特征进行降维。PCA是一种无监督特征变换方法，可以找到最能描述原始数据的特征空间;LDA是一种有监督特征变换方法，目的是找到最能区分各类样本的特征空间[17]。PCA和LDA变换公式分别为

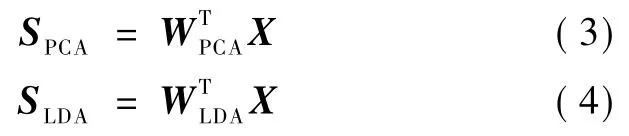
式中：WPCA由样本协方差矩阵的特征向量构成;WLDA由的特征向量构成，Sw为类内散度矩阵，Sb为类间散度矩阵。

1.3 关联向量机

癫痫脑电信号分类是一个有监督机器学习问题。对于一组给定的样本{xi，yi}，i=1，2，…，N，其中xi表示输入向量，yi表示输出值。有监督机器学习的目的是根据训练样本，得到一组权值w，使得对于一个新的输入变量 x*，可以通过模型 f(x，w)，预测其相应的输出值y*=f(x*，w)，有

式中，K(·，·)表示核函数。

关联向量机(relevance vector machine，RVM)是由Tipping等于2001年提出的[14]，在形式上与支持向量机(support vector machine，SVM)类似，如式(7)所示。RVM采用贝叶斯学习框架，为每个权值wi引入一个先验分布，通过最大化后验概率求解超参数。对于0-1二元分类问题，采用 sigmoid函数转化，有

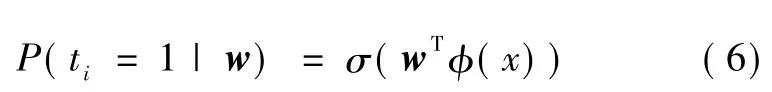
式中，σ(·)表示 sigmoid 函数，σ(μ)=1/(1+e-μ)。

如果直接采用最大似然法通过式(7)对权值进行求解，则得到的模型容易产生过拟合现象，并且得到的模型不够稀疏。RVM与其他方法的不同之处在于：其为每个权值wi引入了一个先验分布，即假设每个wi都服从一个关于超参数αi的零均值分布，即

上述零均值假设对权值起到了限制作用，随着“学习”过程的深入，大部分权值的分布渐渐演化为零附近的δ分布，这些权值对应的基函数即可从模型中删掉，这相当于一个对模型“剪枝”的过程。Tipping的灵感来自于自动关联决策(automatic relevance determination，ARD)，因此 Tipping将在“剪枝”过程中保留下来的基函数所对应的样本称为“关联向量”(relevance vectors)。

RVM处理分类问题时，导出的后验不是正态分布，因此不能得到权值的解析解，为此Tipping采用了Laplace近似。详细的求解过程可参阅文献[14]。

2 材料与方法

2.1 实验数据及预处理

2.1.1 波恩大学癫痫研究中心数据库

为评价所提出的脑电信号分类方法的性能，采用波恩大学癫痫研究中心的脑电数据进行仿真实验[18]。该数据库自建立以来得到了众多研究者的青睐，并渐渐成为癫痫脑电信号分类研究中的“标准数据库”。

数据库包含5组脑电信号(A～E)，每组都有100段脑电信号，每段信号长23.6 s，包含4097个数据点(采样频率为173.61 Hz)，这些脑电信号段截取自连续的脑电信号，在截取之前经过了人工伪迹去除。A组和B组分别是健康志愿者睁眼和闭眼时的脑电信号。C、D、E取自5位癫痫患者术前的脑电信号，C组和D组记录的是癫痫患者发作间期的脑电信号，只是电极放置的位置不同，E组记录的是癫痫发作时患者的脑电信号。顺承Ubely、Lima、Subsai等的研究[4，10，12]，笔者将主要研究 A 和 E 两组脑电信号的分类。为了更好地检验基于AR模型和RVM的癫痫脑电信号分类方法的性能，将每段脑电信号截成4段(每段含1024个数据点，约为5.9 s)。这样，共得到A类脑电信号400段，E类脑电信号400段，即两类样本各400例，样本比例1∶1。

采用10折交叉验证评价笔者所提出的癫痫脑电信号自动分类方法，验证过程有以下步骤。

步骤1：随机取1/10的 A类样本和1/10的 E类样本，构成测试样本集，余下样本组成训练样本集，计算测试精度。

步骤2：随机选取另外1/10的A类样本和E类样本，构成测试样本集，余下的样本组成训练样本集，计算测试精度。

步骤3：重复步骤2，直至遍及每个样本。

步骤4：将10次实验的平均测试精度作为最终测试精度。

其中，随机化处理是为了使训练样本集更具代表性，不会对最终测试结果造成影响。

2.1.2 脑电信号预处理

在特征提取之前，首先对脑电信号预处理。预处理包括脑电信号的平稳化和归一化。采用差分法对脑电信号平稳化，差分平稳化表达式为

式中，{xt}是原始脑电的时间序列，{yt}是平稳化后的时间序列。为了在计算机运算过程中提高运算精度，减小舍入误差对最终结果的影响，进一步对{yt}归一化，归一化公式为

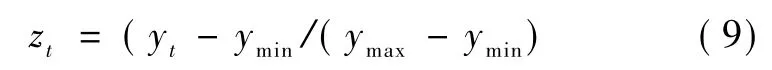
2.2 脑电信号特征提取

根据AIC信息准则，AIC取得最小值时对应的p值为最优p值，此时AR模型对时间序列的拟合程度最好。仿真结果显示，A和E两组脑电信号的最优p值多在20～40之间，因此笔者选用 AR(30)进行脑电信号的特征提取，参数估计方法为Burg法。

2.3 特征变换

引入特征变换方法，降低特征空间维数。在将特征空间维数降至二维时，两类样本的分布情况如图1所示。其中，(a)采用PCA进行特征变换，(b)采用LDA进行特征变换。由图1可以发现，经过特征变化后，即使是在二维特征空间，两类样本仍具有良好的线性可分性。因此，在癫痫脑电信号分类研究中，特征变换的引入是十分必要的。

2.4 分类器

选用SVM作为RVM的比较方法。如前所述，SVM是目前应用最为广泛的一种机器学习方法，并且在脑电信号分类研究中也取得了较高的分类精度。对于这两种核方法，核函数和核参数的选择是十分重要的。选用如下高斯核函数，即

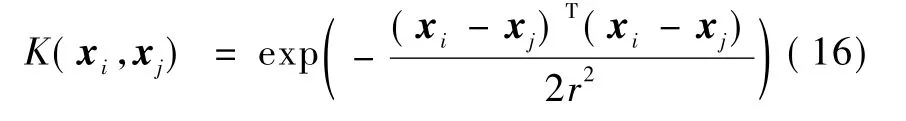
式中，r为核宽，xi和xj均表示列向量。

在这两种核方法中，最优核宽都需要通过交叉验证确定。对于癫痫脑电信号分类，通过10折交叉验证确定模型最优核宽有以下步骤。

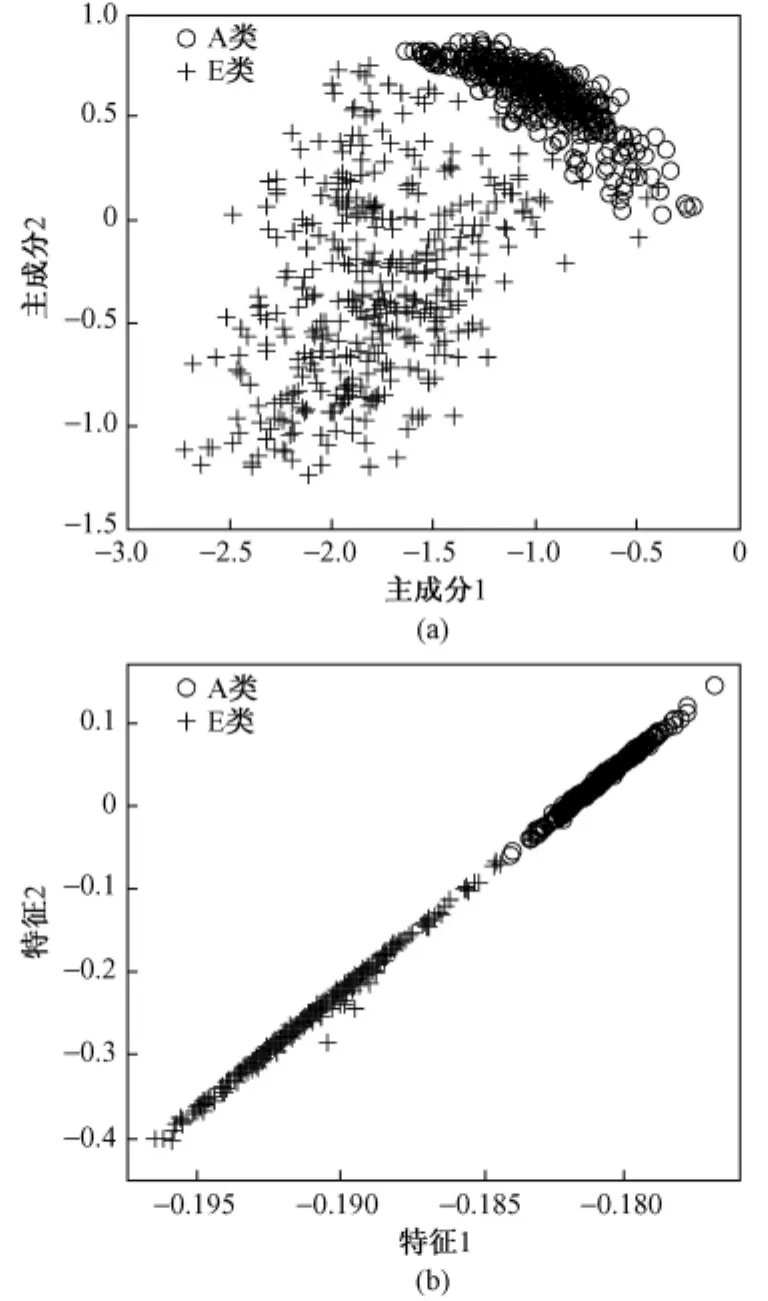
图1 特征变换后，两类样本的分布情况。(a)采用PCA降低特征空间维数;(b)采用LDA降低特征空间维数Fig.1 Samples distribute on 2-D feature space.(a)The dimensionality of feature space is reduced by PCA.(b) The dimensionality of feature space is reduced by LDA

步骤1：随机选取1/10的样本作为测试样本，其余样本为训练样本。

步骤2：对训练样本进行特征变换，并得到变换矩阵 WPCA和 WLDA。

步骤3：使用特征变换后的训练样本、训练分类器。

步骤4：采用步骤2中的特征变换矩阵，将测试样本映射到新的特征空间，并在新的特征空间中计算分类精度。

步骤5：随机选取另外1/10样本作为测试样本，其余样本作为训练样本，重复步骤2～步骤4，直至循环结束。

步骤6：计算 10折交叉验证平均测试精度ma(r)。按如上步骤计算核宽r取不同值时对应的ma(r)，并将ma(r)达到最大值时对应的核宽定义为分类器的最优核宽。

3 结果

为了综合评价所提出的脑电信号分类方法的性能，分别采用 PCA(2)、PCA(5)、LDA(2)、LDA(5)等方法进行脑电信号的特征变换，降低特征空间维数。其中，PCA(2)是指采用 PCA进行特征空间降维，降维后的特征空间维数为二维，其他如PCA(5)、LDA(2)、LDA(5)含义类同。

图2 基于SVM的癫痫脑电信号分类。(a)基于全部特征和基于二维特征的分类结果;(b)基于全部特征和基于五维特征的分类结果Fig.2 EEG signal classification for epilepsy based on SVM.(a)Based on all 30 features and 2 features.(b)Based on all 30 features and 5 features

采用支持向量机作为分类器，分类精度随核宽参数j的变化情况如图2所示。其中，分类精度是指10折交叉验证最终的测试精度，(a)是基于全部特征(30维)和基于二维特征的分类精度比较，(b)是比较了基于全部特征(30维)和基于5维特征的分类结果。核宽与核宽参数j的关系为：r =(j=-5，-4，…，12)。核宽参数j的引入是为了在较大范围内寻找最优核宽，D表示降维后特征空间的维数的引入仅仅是为了便于在同一图内比较降维幅度不同时的分类结果。

图3 基于RVM的癫痫脑电信号分类。(a)基于全部特征和基于二维特征的分类结果;(b)基于全部特征和基于五维特征的分类结果Fig.3 EEG signal classification for epilepsy based on RVM.(a)Based on all 30 features and 2 features.(b)Based on all 3O features and 5 features

采用关联向量机作为分类器，分类精度随核宽参数j的变化情况如图3所示。同采用支持向量机作为分类器时的情况一样，(a)是基于全部特征(30个)和基于二维特征时分类精度的比较，(b)是基于全部特征(30个)和基于五维特征时分类精度的比较。在图3中，核宽和核宽参数的定义与采用支持向量机作为分类器时的定义相同。

表1比较了上述各模型在取最优j值时模型的特征空间维数、稀疏性和分类精度。由于主要研究基于关联向量机的癫痫脑电信号分类，因此在表1中增加了两组仿真实验：PCA(15)+RVM和 LDA(15)+RVM。

如表1所示，基于不同特征空间维数进行分类时，采用关联向量机作为分类器时得到的分类精度与采用支持向量机作为分类器时得到的分类精度基本相当，但是模型稀疏性大幅度提高(平均关联向量数为：3.64，平均支持向量数为：171.32)。这意味着采用关联向量机作为分类器时，模型训练后仅根据几个关联向量即可确定分类边界，因此测试速度大幅度提高。在癫痫脑电信号自动分类系统中，测试速度是十分重要的。

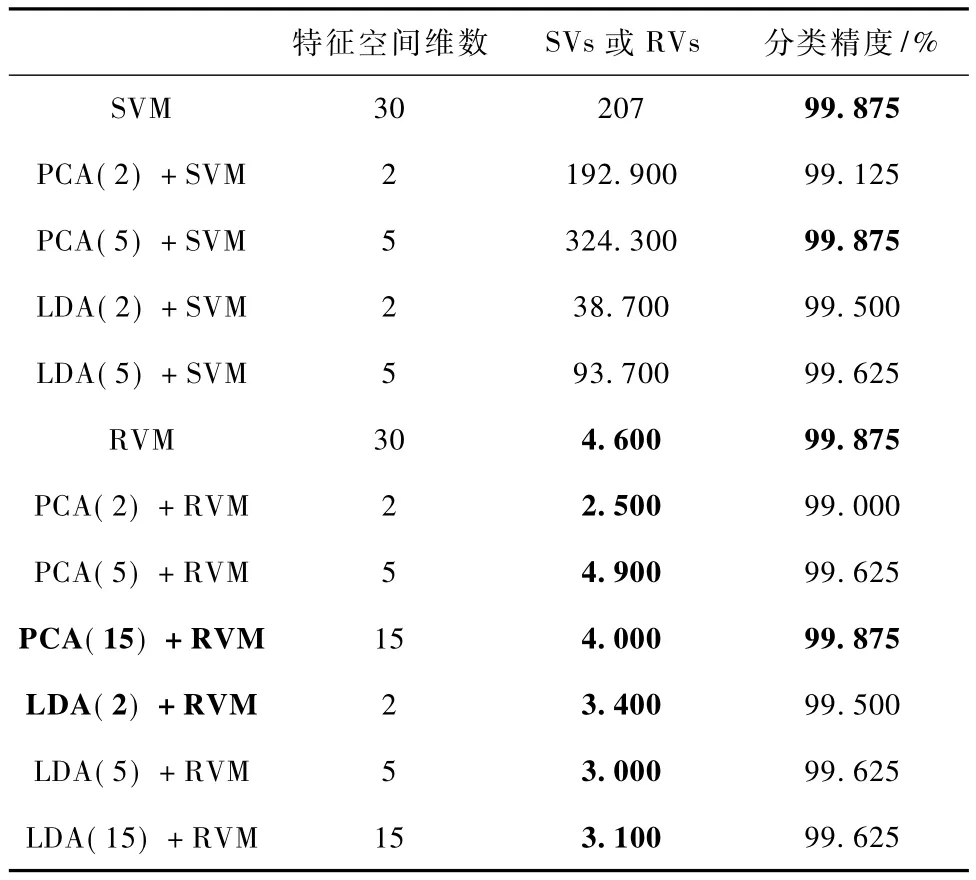
表1 最优核宽(j值)下模型性能Tab.1 Performance of different EEG signal classification methods with best kernel widths

特征变换方法的引入，可以使模型在保持较高分类精度的同时，有效降低特征空间维数。LDA(2)+RVM在将特征空间维数降为原始维数的1/15时，仍可以保持较高的分类精度(99.500%)。PCA(15)+RVM在将特征空间维数降为原始维数的1/2时，仍可以达到最高的分类精度(99.875%)。当需要对特征空间进行较大幅度降维时，LDA更适用;当需要在保证模型分类精度的同时降低特征空间维数时，PCA更适用。此外，由于经过LDA特征变换，两类样本具有良好的线性可分性，见图1(a)，因此基于LDA的分类方法对核参数的敏感性降低(见图1和图2)。

在表2中，将本研究所提出的癫痫脑电信号自动分类方法与近年来一些同类方法进行了比较，这些方法都采用波恩大学癫痫研究中心的A和E两组脑电信号。比较发现，本研究所提出的癫痫脑电信号自动分类方法可以达到较高的分类精度。

4 讨论和结论

本研究提出了一种基于自回归模型和关联向量机的癫痫脑电信号自动分类方法，主要探究了在癫痫脑电信号自动分类系统中引入特征变化方法，讨论了采用关联向量机作为分类器的可行性。

表2 与其他研究的比较Tab.2 Comparison of classification accuracy with other researches'

传统癫痫脑电信号自动分类方法往往直接将提取得到的脑电信号特征输入到分类器，而本方法则先对特征空间降维，再将降维后的脑电信号特征输入到分类器。研究结果显示，即使是将特征空间维数降至原始维数的1/15或者1/6，最终结果仍可以达到较高的分类精度。这说明，提取得到的原始脑电信号特征包含了大量的冗余信息，对原始脑电信号特征进行特征变换，进一步精炼有价值的分类信息，对于癫痫脑电信号自动分类系统的研究是十分有意义的。

关联向量机是比支持向量机更为稀疏的核模型，并且可以得到概率式输出，这些特点使得关联向量机非常适合应用于癫痫脑电信号分类。本研究表明，在癫痫脑电信号分类系统中选用关联向量机作为分类器，可以在保证较高分类精度的同时，大幅提高模型的稀疏性。这表明，关联向量机可以很好地用于癫痫脑电信号分类系统。

基于自回归模型和关联向量机，实现了癫痫脑电信号的自动分类。结果显示：本研究所提出的癫痫脑电信号分类方法可以达到较高的分类精度(99.875%);特征变换方法的引入可以有效降低特征空间维数，降低模型对核参数的敏感性;采用关联向量机作为分类器，可以在保证较高分类精度的同时，显著提高模型稀疏性。

综上所述，本研究提供了一种性能良好的癫痫脑电信号自动分类方法。该方法将特征变化引入到癫痫脑电信号自动分类系统，为癫痫脑电信号自动分类系统提供了一种三步式的设计思路：特征提取，特征变换，分类器。与传统的两步式(特征提取，分类器)设计思路相比，本方法更加科学合理、易于实现。本研究尝试了将关联向量机用于癫痫脑电信号分类系统的可行性，结果表明关联向量机可以很好地应用于癫痫脑电信号分类系统。

[1]Alkan A，Koklukaya E，Subasi A.Automatic seizure detection in EEG using logistic regression and artificial neural network[J].Journal of Neuroscience Methods，2005，148：167-176.

[2]Subasi A，Alkan A，Koklukaya E，et al.Wavelet neural network classification of EEG signals by using AR model with MLE preprocessing[J].Neural Network，2005，18：985-997.

[3]Chisci L，Mavino A，Perferi G，et al.Real-Time Epileptic Seizure Prediction Using AR Models and Support Vector Machines[J].IEEE Trans on Biomed Eng，2010，57：1124-1132.

[4]Ubeyli ED.Least squares support vector machine employing model-based methods coefficients for analysis of EEG signals[J].Expert Systems with Applications，2010，37：233-239.

[5]Han Min，Sun Leilei.EEG signal classification for epilepsy diagnosis based on AR model and RVM[C]//Wang Jun，Han Min，eds.2010 International Conference on Intelligent Control and Information Processing.Dalian，Liaoning，China，2010.134-139.

[6]Guler I，Guler NF，Ubeyli ED.Recurrent neural networks employing Lyapunov exponents for EEG signals classification[J].Expert Systems with Applications，2005，29(3)：506-514.

[7]Aslan K，Bozdemir H，Sahin C，et al.A radial basis function neural network model for classification of epilepsy using EEG signals[J].Journal of Medical Systems，2008，32(5)：403-408.

[8]Acir N，Guzelis C.Automatic spike detection in EEG by a twostage procedure based on support vector machines [J].Computers in Biology and Medicine，2004，34(7)：561-575.

[9]邱天爽，郑效来，鲍海平，等.一种基于支持向量机技术的癫痫脑电棘尖波识别方法[J].生物物理学报，2005，21(4)：317-321.

[10]Lima CAM，Coelho ALV，Chagas S.Automatic EEG signal classification for epilepsy diagnosis with Relevance Vector Machines[J].Expert Systems with Applications，2009，36：10054-10059.

[11]Nigam VP，Graupe D，A neural-network-based detection of epilepsy[J].Neurological Research，2004，26：55-60.

[12]Subasi A. EEG signal classification using wavelet feature extraction and a mixture of expert model[J].Expert Systems with Applications，2007，32：1084-1093.

[13]Aarabi A， Fazel-Rezai R， Aghakhani Y. EEG seizure prediction：measures and challenges[C]//Liang ZP，eds.2009 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minneapolis：Institute of Electrical and Electronics Engineers( IEEE )，2009.1864-1867.

[14]Tipping ME.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research，2001，1：211-244.

[15]邱浪波，王广云，王刚，等.相关向量机在肿瘤表达谱分类问题中的应用[J].中国生物医学工程学报，2008，27(1)：83-86

[16]Box GEP，Jenkins GM.Time series analysis：forecasting and control[M].San Francisco，USA：Prentice Hall publisher，1970.53-66.

[17]邓洪波，金连文.一种基于局部 Gabor滤波器组及 PCA+LDA的人脸表情识别方法[J].中国图象图形学报，2007，12(2)：322-329.

[18]Andrzejak RG，Lehnertz K，Mormann F，et al.Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity：Dependence on recording region and brain state[J].Physical Review E，2001，64(061907)：1-8.