遗传算法工具箱(GOAT)在M TM D参数优化中的应用

2011-08-11禹见达周小波

湖南工程学院学报（自然科学版） 2011年3期

李东,禹见达,金磊,周小波

(湖南科技大学土木工程学院,湘潭411201)

0 前言

结构的振动控制一直是人们关注的焦点,振动控制按其是否需要从外界输入能量,分为主动控制和被动控制[1],虽然主动控制从理论上要比被动控制优越一些,然而目前在工程上应用最多,最成熟的还是被动控制.调谐质量阻尼器是一种应用广泛的被动控制,按其数目分为单个调谐质量阻尼器(TMD)和多重调谐质量阻尼器(MTMD).但TMD对与主结构的频率变化比较的敏感,且一旦频率偏离TMD的固有频率时,减振效果会大大降低.为了扩大其减振频率的范围和更好地控制结构的振动,就需要应用多重调谐质量阻尼器(MTMD).多重调谐质量阻尼器参数优化就是对各个调谐质量阻尼器的阻尼系数,固有频率,以及多重调谐质量阻尼器的TMD数目进行调整,已达到最好的控制效果.

1 多重调谐质量阻尼器减振模型及原理

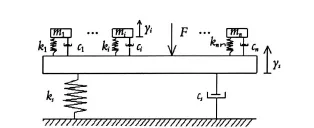
图1 主结构-MTMD系统

如图1所示,有n个调谐质量阻尼器安装在有阻尼(Cs)和刚度弹性(Ks)的主结构上,各个调谐质量阻尼器的阻尼、质量和弹性系数分别为ci、mi和(i=1、2、3、…n),通过安装多重 TMD 来抑制结构过大振动.

1.1 主结构-MTMD系统模型运动方程式

图1所示的主结构-MTMD系统的运动方程为:

其中y是位移向量,包括主结构的位移ys和各个调谐质量阻尼器的yi.即

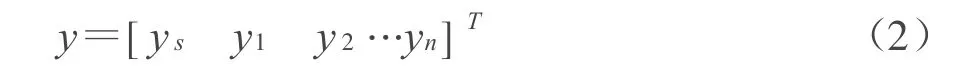
M、C和K分别是质量,阻尼和弹性系数矩阵.

1.2 结构响应的动力放大系数

为了获得主结构反应的DMF(动力放大系数),假设外力荷载为调谐荷载且作用在主结构上,则外力荷载F向量可表示为:F=f0eiωt[1 0 0 L 0]T,f0是外荷载的幅值,ω是外荷载的频率.

因此,根据动力学原理,主结构的动力放大系数(DMF)最终可以由以下公式求得:

(3)式中:

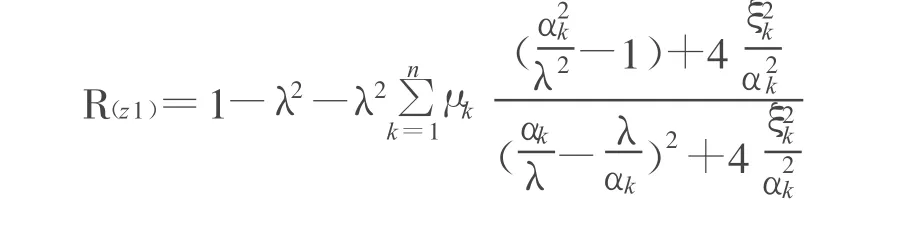
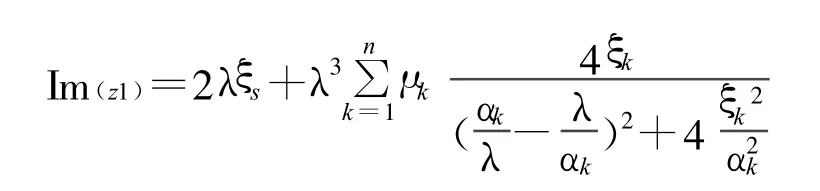
ω、ωs和ωk分别是外荷载、主结构和第 k个 TMD 的频率;mk、ms分别是第k个TMD和主结构的质量;ck和cs分别是主结构和第k个TMD的阻尼系数.

2 MATLAB遗传算法工具箱(GOAT)的MTMD参数优化

2.1 MAT LAB遗传算法工具箱(GOAT)

遗传算法[2](Genetic Algorithm,简称GA)是美国Holland教授首先提出来的,是一种基于基因遗传原理和自然选择的优化搜索方法.相对于其他优化算法,遗传算法有自身独特的特点和优越性[3],因此在各个领域都得到了广泛的应用.遗传算法在使用的过程中要编制大量的程序,但对于一般的使用者只希望使用现有程序优化得到需要的结果,MATLAB遗传算法工具箱(GOAT)可以直接调用工具箱里面现有的程序,解决实际问题,这给使用者节省了大量的时间和工作量,遗传算法工具箱很快被应用于解决许多实际优化问题.

2.2 遗传算法工具箱的MTMD参数优化

实际工程中,许多结构的频率在使用过程中并不是固定的,而是变化的,而且这种变化是不能忽略的.在考虑主结构频率在一定范围内变化的情况下,通过调用遗传算法工具箱(GOAT),得到适合主结构频率一定范围内变化的质量均匀分布的MTMD最优参数,实现了主结构的变频率最优MTMD振动控制.

图2 最优控制图

图2是在TMD数目N为10,单个TMD质量比 =0.001和主结构频率 ω=1.0,阻尼ξs=0.002情况下,得到优化参数后保持其他参数不变,并考虑主结构不同频率时的DMF控制图.

图3 频率变化的最优控制图

由图2可知一旦主结构频率发生偏移时,DMF的峰值都会突然增大,控制效果明显变差,根本达不到控制振动的效果,因此,在固定主结构频率条件下优化得到MTMD参数是不能满足主结构频率变化的使用要求的.为此要寻找一组最优MTMD参数值,使其主结构频率变化时也能达到很好的控制效果.图3是在TMD数目N为10,单个TMD质量比μk=0.001和主结构频率ωs=1且考虑变化范围为±3%,阻尼ξs=0.002的情况下,使用遗传算法工具箱优化(GOAT)得到的DMF最优控制图;从图中可以看出,虽然DMF的峰值相对于不考虑主结构频率变化的的峰值要大一些,但是其对主结构频率变化的敏感性明显降低,鲁棒性明显优化了很多,因此,在考虑主结构频率变化后优化得到的MTMD参数更加适用于实际工程的使用.

图4 方差曲线

图5 方差曲线

为了分析主结构频率为1,阻尼为0.002,均匀分布的MTMD总质量比为0.01在不同N值(N=2、3、5、10 、15、20),考虑不同频率变化范围(±1%、±2%、±3%、±4%),通过10次搜索优化的情况选择一个最优的作为最优解,先定义DMF峰值 x±i,方差σi,平均值及最大值 Xmax.即 x±i为考虑频率偏差±i%时所对应的DMF峰值,σi为主结构频率变化±i%时的方差值是主结构频率变化±i%时DMF峰值的平均值,Xmax为考虑频率偏差±i%时所对应的DMF峰值中的最大值.涉及到的计算公式如下:

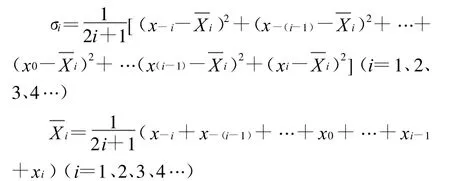
图4、图5反映了频率变化范围不同时,σ值的变化情况(横坐标是TMD的数目 N值),频率变化范围小得到的σ值越小,因此,更容易接近于最优解,当频率偏差过大时,σ值随之变大,DMF的峰值稳定性变差,要得到较好的解必须要通过多次搜索运算比较,才能保证其比较接近于最优解.而对于每一组频率变化情况下得到的σ曲线变化趋势,在 N等于5之前变化显著,后面变化趋于平缓.说明了过大追求N值并不能有效地控制结构的振动.

由以上的分析可以得出:质量均匀分布的M TMD在某一种结构上(文章是主结构频率为1,阻尼为0.002),考虑主结构频率变化时优化得到的M TMD参数对主结构频率变化的敏感性大大降低,鲁棒性更好;引入σ值,分析了各个DMF峰值的偏差性,结果显示,主结构变化范围越小,偏差越小,同时对于TMD个数N是越大偏差越小,但当数目N超过5时,变化不再明显,σ值越小,说明参数越接近于最优解.当σ值偏大时,要增加搜索优化次数,从而确定其优化参数值.