库水位下降时土坝上游面渗流稳定性研究

张大伟，严文群

（1.连云港市石梁河水库管理处，江苏连云港 222323；2.扬州大学水利科学与工程学院，江苏扬州 225009）

库水位下降时土坝上游面渗流稳定性研究

张大伟1，严文群2

（1.连云港市石梁河水库管理处，江苏连云港 222323；2.扬州大学水利科学与工程学院，江苏扬州 225009）

大坝迎水坡的最不利工况是长期蓄水（高水位运行）后水位骤降，影响此时上游坡土体稳定性的因素有水位降落速度、土体特性等。借助于渗流分析软件Geoslope和unsst2，不仅从渗流稳定性出发，说明了坡面渗水的危害；从防止大坝上游坡在库水位下降时产生自由溢出点出发，拟合了不同k／μv时库水位下降的临界高度；而且考虑了由于各种原因产生的土体各向异性和基质吸力摩擦角φb对上游坝坡稳定性的影响。研究表明，对于库水位下降时上游坡稳定性分析，尤其应结合渗流场计算结果，同时考虑工程实际中各种因素的影响。

库水位下降；渗流稳定性；坡面出渗临界坡降

1 概 述

大坝迎水坡的最不利工况是长期蓄水（高水位运行）后水位骤降，此时极易发生滑坡破坏。由于坝体土体排水能力的限制，坝内地下水浸润面无法与库水位下降速度同步，坝体中央易出现高水头区。此时地下水渗流由最初稳定渗流场时的上游流向下游，转变为由坝体中央高水头区分别向上游和下游流动，分别在上游坡和下游坡产生出渗点。根据文献［1］提出的自由出渗点处渗流临界坡降计算公式可知，对于内摩擦角35°的砂子，允许渗透坡降为0.3左右，坝坡应缓于1∶3。因此应尽量减少渗流自由出渗或在渗流出口处布置排水反滤（土工布及颗粒滤层）及压重。

对于库水位降落条件下的大坝渗流计算国内外普遍以相对比值k／μv作为判别降落快慢的依据。其中k为渗透系数；μ为给水度；v为水位降落速度。施特尼通过试验认为，k／μv＜0.1时，自由面下降缓慢，可以按骤降考虑问题，当k／μv＞10时，孔隙水与库水位同步下降，渗流对稳定影响较小。乌里希研究了骤降和缓降时k／μv的范围，认为骤降时应放宽至0.25，缓降应放宽至100，国内学者［1］将缓降指标放宽至60。尽管如此，国内外对k／μv与渗透坡降关系及库水位降落时上游坡渗流局部稳定性研究仍较少，本文对此做了一些模拟研究。

由于施工造成的土体渗透系数各向异性极大地影响了渗流场分布［2］，本文将此影响作为辅助因素予以考虑。同时本文也研究了饱和-非饱和抗剪强度理论中的基质吸力摩擦角φb对上游坡稳定性的影响。总之尽可能全面细致地研究库水位下降时上游坡渗流稳定性。

2 非稳定渗流微分方程式

考虑土体和水的压缩性，基于质量守恒定律和达西定律，推导出的非稳定渗流微分方程式为

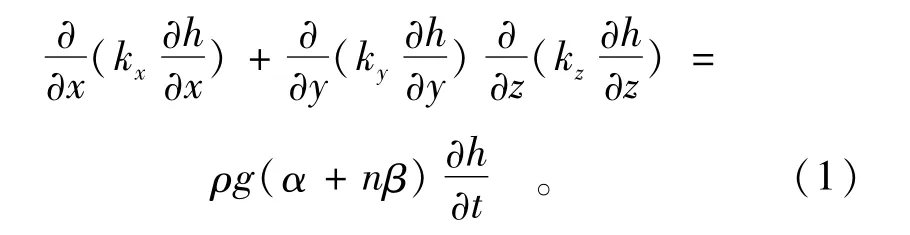
式中：α为土体的压缩模量；β为水的压缩模量，Ss＝ρg（α＋nβ）定义为单位贮存量；n为孔隙度。

各向同性土体忽略水的压缩性时，Ss＝ρgα，式（1）简化为

式（2）又被称为非稳定渗流的固结方程。

3 模型分析

3.1 非稳定渗流场分析

均质土坝尺寸如图1所示。下游无水，稳定渗流场时上游水位20 m，非稳定渗流（库水位下降）时库水位由最初的20 m最终降落至库底。采用的3种筑坝材料见表1，此3种材料由Geoslope软件的examples（材料库）提供，用Geoslope软件计算库水位下降时的非稳定渗流场。3种筑坝材料各计算3个降落速度，共9种计算工况。计算参数见表1。

给水度μ按照毛昶熙［1］公式

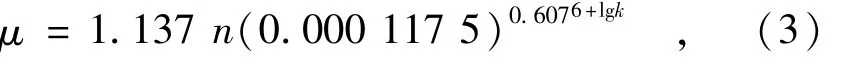
式中k的单位为cm／s。

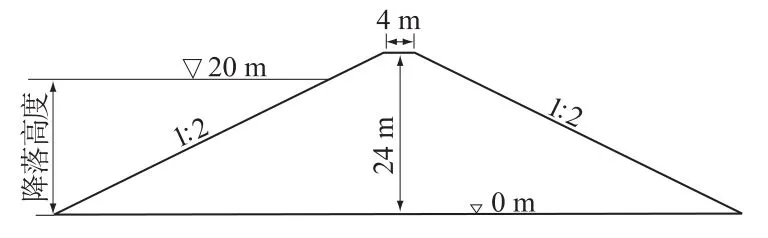
图1 土坝示意图Fig.1 Sketch map of earth-rockfill dam

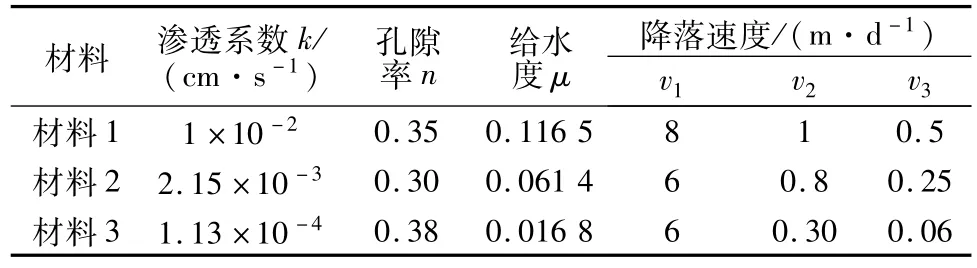
表1 计算参数表Table 1 Calculation parameters

9种工况对应的k／μv值与1，5，10，20，40，80，100，120，150接近。

库水位下降期间，当浸润线下降速度无法与库水位相一致时，在上游坡面上产生溢出点，没有反滤层保护时易发生局部破坏。同时水面线与坡面线的交点处也是局部渗透破坏的多发区。同理有二元结构的堤防汛期结束时河道水位急剧下降，地下水在下卧砂层坡面产生溢出点。溢出点和水面线的砂子极易产生渗透破坏，沿着坡面向下滑动，极易造成土体局部失稳，甚至酿成滑坡险情。

堤坝渗流局部稳定性分析主要是计算坝坡渗流溢出点处的渗透坡降，并与允许渗透坡降进行比较，当计算值大于允许值时土体发生渗透破坏。水闸设计时还应判断基础产生接触冲刷的可能性。

库水位从20 m下降到0 m的过程中，浸润线分水岭和渗流溢出点之间的平均水平向渗透坡降与k／v，k／μv的关系曲线见图2、图3和图4。

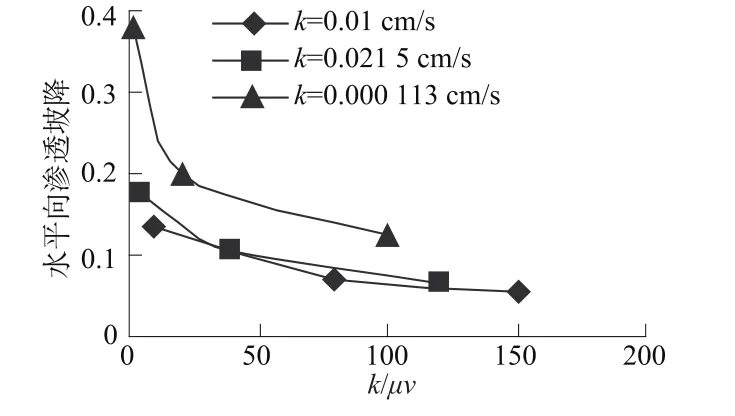
图2 不同材料k／μv-水平向渗透坡降关系图Fig.2 k／μv of differentmaterials versus the horizontal seepage gradient

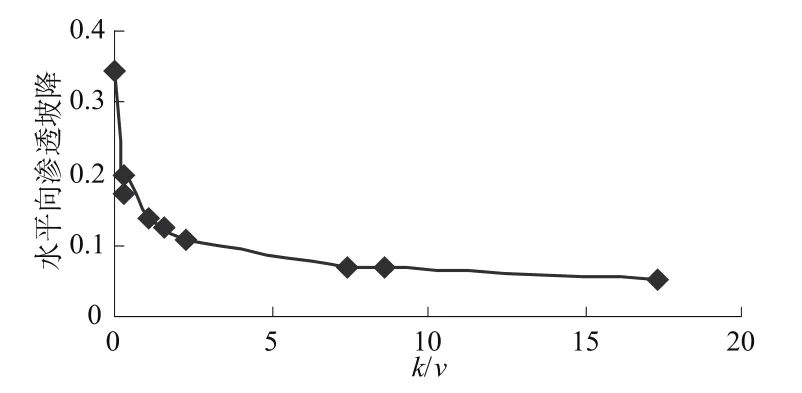
图3 k／v-水平向渗透坡降关系图Fig.3 k／v versus horizontal seepage gradient

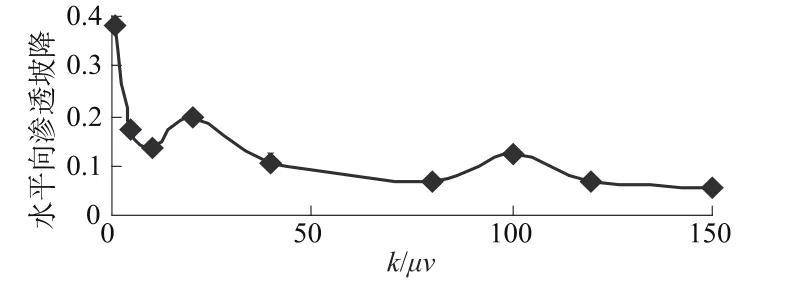
图4 所有k／μv-水平向渗透坡降关系曲线Fig.4 k／μv of allmaterials versus horizontal seepage gradient

图2 可以看出库水位下降时，水位降落速度越快（同种筑坝材料不同降速），浸润线与上游坡面溢出点间的的平均水平向渗透坡降大；渗透系数越小（不同筑坝材料相同降速），水平向渗透坡越大。图3可以看出库水位下降期间浸润线与上游坡面溢出点间的的平均水平向渗透坡降与k／v大致成反比关系，k／v越大水平向渗透坡降越小。从9种计算工况的水平向渗透坡降绘制成的图4可以看出对于饱和-非饱和理论而言，土水特征曲线的确定是至关重要的。饱和渗透理论计算非稳定渗流在浸润线变化区域给定流量补给边界条件（参数为给水度μ），计算区域在变化。饱和-非饱和理论计算区域是固定的，饱和区、非饱和区土壤的渗透系数与水压力或基质吸力的关系被称为土水特征曲线，因此确定给水度-土水特征曲线的关系值得深入研究。

Geoslope软件计算以上3种材料共计9种降落速度时大坝渗流，得到上游坡溢出点坡降在0.36～0.49之间（理论值为0.45），计算模型中的材料1、材料2（中细砂）的摩擦角在30～35°，其允许渗透坡降在0.1～0.3之间，即水位下降期间上游坡渗出点处易发生局部渗透破坏［3］。

当模型坝选用材料1填筑，初始水位为20 m，以1 m／d的降落速度历时20 d时（k／μv＝74.16），均匀选取11个时刻计算瞬态渗流场，浸润线见图5。图5可以看出当库水位降至10 m以下后坝体内产生高压区，浸润线上存在一分水岭。水位下降至2 m之前的所有时刻上游坡与水面线交点以上坡面未产生溢出点，浸润线和上游坡及水面线交于同一点，此时可以认为是缓降。

以上3种材料，9种库水位下降过程浸润线产生分水岭时水位下降值占初始上游水深（20 m）的比值与k／μv关系见图6。

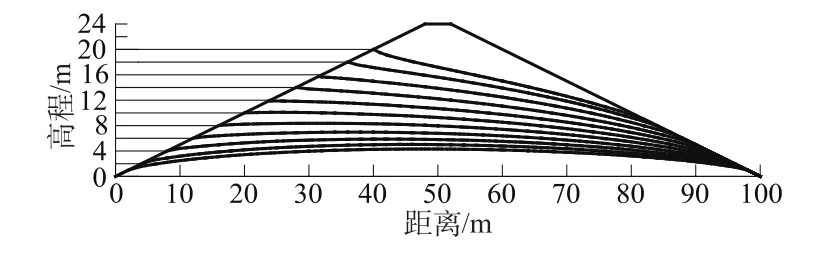
图5 缓降时非稳定渗流场图Fig.5 Unsteady seepage field under slow drop

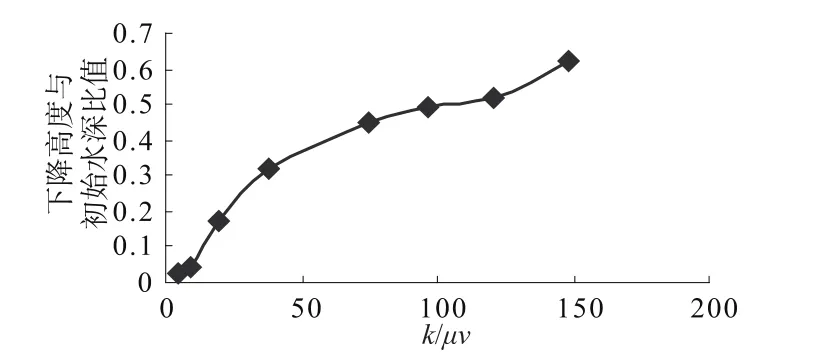
图6 下降高度与初始水深比值与k／μv关系图Fig.6 Drop height／initialwater level versus k／μv

当相对下降高度在图6中曲线下方时，浸润线不会产生分水岭，上游坡面不会出现溢出点，对上游坡稳定性影响不大。当水位下降高度大于图6所示的临界下降高度时，浸润线出现分水岭，坝体水分从分水岭分别向上游下游流动，随着库水位的下降，并伴随着坡面上产生自由出渗面，上游坡稳定性显著下降。库水位下降时的上游坡由于易出现渗流溢出点、较大的水平向渗透坡降和较高的坝体孔隙水压力，所示易出现局部渗流破坏，应采取渗流控制措施。

3.2 上游坡渗流稳定性分析

以kx＝ky＝2.15×10－3cm／s（材料2），n＝0.30，c＝0 kPa，γs＝20 kN／m3，γ干＝15 kN／m3的材料2为例，库水位下降速度为0.8 m／d时，k／μv＝37.8。库水位从20 m到0 m间隔2 m的11个瞬态渗流场浸润线如图7所示，渗流局部稳定性用公式（4）验算，整体稳定性分析结合渗流计算的坝体孔隙水压力值验算上游坝坡稳定性。由

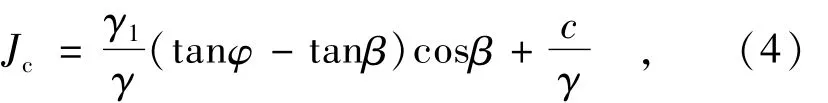
计算得到溢出点最大允许渗透坡降Jc＝0.18。库水位下降至10 m以下时上游坡产生溢出点，库水位下降期间溢出点渗透坡降计算值见表2。

表2 溢出点渗透坡降J表Table 2 Seepage gradient of spill point

从表2可以看出水位下降至10 m以下后，渗出点处土体在渗透力作用下起动并沿着坡面下滑，实际工程中应在溢出点以上铺设土工布并用块石压重。库水位与上游坡抗滑稳定系数［4］关系见图8。

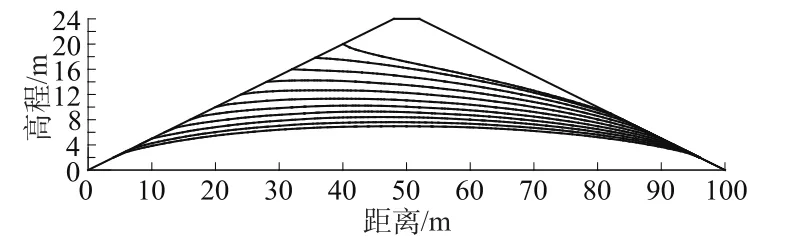
图7 下降速度为0.8 m／d时的浸润线图Fig.7 Saturation lines when the dropping speed is 0.8 m／d

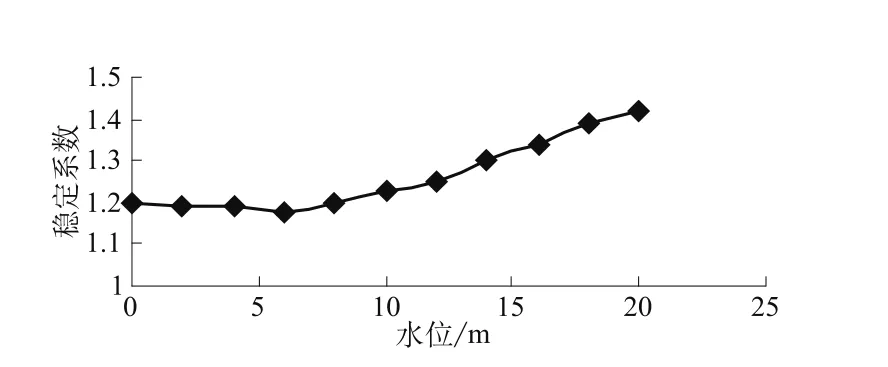
图8 v＝0.8 m／d时库水位与抗滑稳定系数关系图Fig.8 Curve of water level versus anti-sliding stability coefficient when v＝0.8 m／d

Geoslope软件计算结果此时上游坡即使发生滑坡也是浅层滑坡，此时库水位降落速度并未达到骤降标准（此时k／μv＝37.8）。故文中没有将危险滑动面画出，从表2计算值可以看出此时大坝上游坡主要的问题是溢出点发生局部渗透破坏。若渗流出口处没有保护措施，随着库水位的下降这种局部破坏会逐渐发展，坝体材料为砂子时表现为砂子在地下水渗流力作用下成块状塌落，形成浅层滑坡，类似于河道上的崩岸［5］险情。

3.3 各向异性对渗流场影响研究

岩土体透水性不均匀的现象普遍存在。天然的岩土不同程度上存在着各向异性的现象，对于岩石造成这种非均匀透水性主要是由于层理的存在及其走向不同、颗粒组成和结构上的不同及孔隙和裂隙的发育不均匀等。冲积层土在天然沉积过程中，水平透水性经常是垂直透水性的2～10倍，天然黏土野外原地试验表明，水平透水性一般比垂直大3～5倍。分层碾压也会使坝体渗流系数产生各向异性现象。羊角碾碾压时，堤坝横向渗透系数kx与纵向渗透系数ky之比为2～10。用气胎碾碾压时，kx与ky之比为20～30。以发生溃坝事故的青海省沟后面板砂砾石坝为例，事后调查坝体的各向异性倍数达到了45。正确考虑土体存在的这种透水性不均匀现象很重要。

3.3.1 各向异性对稳定渗流场影响分析

以ky＝2.15×10－3cm／s，n＝0.30，c＝0 kPa，γs＝20 kN／m3，γ干＝15 kN／m3的材料2为例。

kx／ky分别为1和10时，上游水位20m，下游无水稳定渗流场浸润线如图9所示。

图9 kx／ky分别为1和10浸润线Fig.9 Saturation lines when kx／kyis 1 and 10 respectively

从图9可知，kx／ky＝10较kx／ky＝1稳定渗流场的浸润线有所抬高，对下游坝坡的渗流局部稳定性造成不利影响，等势线更加向上游倾斜，同一垂直断面上下部水头明显小于上部水头，坝体地下水明显存在垂直向下的流速。理论上来说对渗流整体稳定性是有利的，但由于水平向渗透系数增加坝体渗流量，同时大坝管理单位若按照各向同性计算的溢出高度保护下游坡那将变得很危险。

3.3.2 各向异性对非稳定渗流场影响分析

由kx／ky＝10（ky＝2.15×10－3cm／s），库水位降落速度v＝0.8 m／d，降落时间为25 d，均匀截取水位从20 m到0 m的11个瞬态时刻的渗流场浸润线绘制成图10，不同水位时上游坡稳定系数绘制成图11。

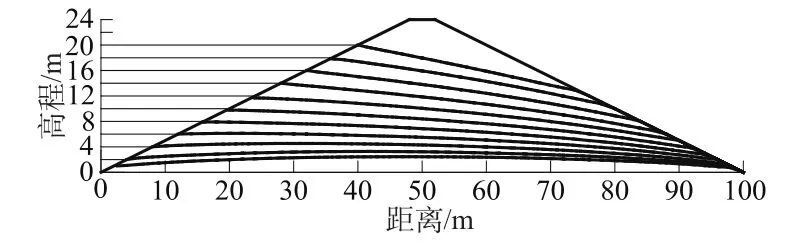
图10 kx／ky＝10时各时刻浸润线图Fig.10 Saturation lines at each moment when kx／ky＝10

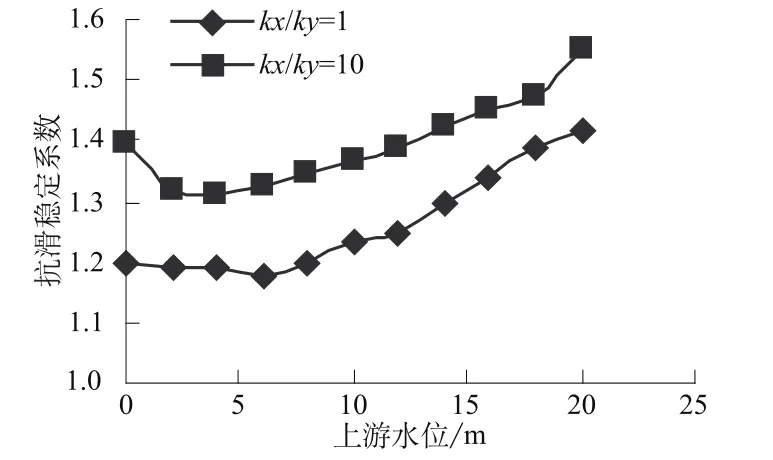
图11 不同kx／ky时水位-抗滑稳定系数关系曲线Fig.11 Curves of water level versus anti-sliding stability coefficient under different kx／ky

从图10、图11可以看出，保持垂直向渗透系数ky不变，增大水平向渗透系数时，库水位下降过程中上游坡稳定性增加，各向异性材料坝体上游部分孔隙水压力消散的比各向同性快，在库水位由12 m到0 m过程中，当kx／ky＝1时，浸润线分水岭高度分别为12.368，11.050，9.988，9.085，8.293，7.575，6.999 m；当kx／ky＝10时，分别为12，10，8，6，4.302，3.223，2.503 m。库水位下降至4 m之前kx／ky＝10的浸润线都能与水面线相交，而kx／ky＝1在库水位下降至12 m以下后就在上游坡产生了渗流溢出点。kx／ky＝10浸润面下降的较kx／ky＝1为快。各向同性材料和各向异性材料在垂直断面上水头分布也是有差别的，各向异性渗流场地下水有向下流动的趋势，整体稳定性增强。

3.4 φb对非稳定渗流影响分析

饱和-非饱和土渗流理论出现同时，Fredlund和Morgenstern两位专家提出了渗流、边坡稳定方面的非饱和土体抗剪强度理论。此理论考虑了浸润线以上土体的基质吸力的影响，可以有效地解释降雨期间滑坡产生的原因，降雨期间随着非饱和土体基质吸力的减小，抗剪强度明显下降，上部土体重度增加、滑动力增加，土体的抗滑力较小，最终造成滑坡破坏。

Fredlund-Morgenstern抗剪强度公式为

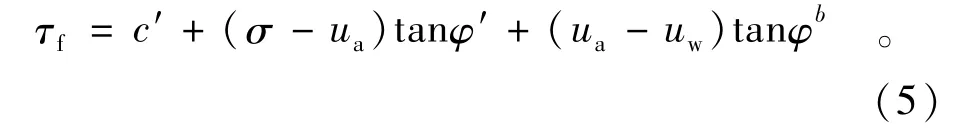
式中：τf为极限抗剪强度；c′为黏聚力；φ′为有效内摩擦角，σ为剪切面上法向压应力；ua为孔隙气压力；uw为孔隙水压力；参数φb作为吸力ua-uw的内摩擦角，早期人们假定φb是一个定值，后来许多学者从试验中发现φb是基质吸力的函数，当土体接近饱和时，φb接近于饱和土的内摩擦角。当土体饱和度降低时，基质吸力增加φb逐渐减小。φb随着基质吸力的增大而减小。

以材料2为例，kx＝ky＝2.15×10－3cm／s，n＝0.30，c＝0 kPa，φb＝18°和0°，φ′＝35°，γs＝20 kN／m3，γ干＝15 kN／m3。库水位降落速度为0.8 m／d，水位从20 m降落至0 m，共25 d。均匀截取水位从20 m到0 m共11个工况的瞬态抗滑稳定安全系数［6］绘制成图12。

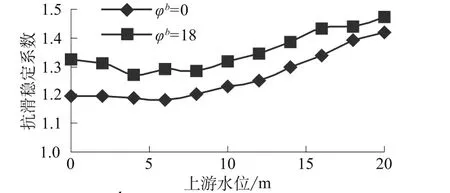
图12 不同φb时水位与抗滑稳定系数关系曲线Fig.12 Curves of water level versus anti-sliding stability coefficient under differentφb

从图12可以看出由于选用了较大的φb考虑浸润线以上天然状态土体的基质吸力的有利作用，库水位下降期间稳定系数较不考虑基质吸力内摩擦角为大。抗滑稳定安全系数最大上升了近10%。

4 结 论

（1）库水位下降时由于水体的压重作用消失，上游坡易在渗流溢出点和水位波动点产生局部破坏，砂质坝体易随水位下降产生块状坍落，最终形成浅层滑动。当库水位下降过快时（骤降）坝体孔隙水压力来不及消散，上游坝坡溢出点很高，往往会发生深层的整体滑动。

（2）对于土体水平向渗透系数较垂直向为大（主要是地质构造、沉积过程、施工碾压的原因）的土坝，其坝体渗漏量较均质坝体增大，浸润线有所抬高，对大坝下游坡渗流局部稳定性不利，当库水位下降时的上游坡整体稳定性却有利，应综合考虑。

（3）考虑基质吸力内摩擦角后大坝稳定性有所增加，但实际应用中难于准确获取φb值的大小。

［1］ 毛昶熙.渗流计算分析与控制［M］.北京：中国水利水电出版社，2003.（MAO Chang-xi.Seepage Computation Analysis＆Control［M］.Beijing：ChinaWater Power Press.2003.（in Chinese））

［2］ 黄永健，高季章，贾金生，等.崩岸整治新技术试验工程的设计与施工［J］.中国水利水电科学研究院学报，2003，（1）：23－29.（HUANG Yong-jian，GAO Ji-zhang，JIA Jin-sheng，et al.Design and Construction of Pilot Projects for Levee-Bank Collapse Treatment［J］.Journal of China Institute of Water Resources and Hydropower Research，2003，（1）：23－29.（in Chinese））

［3］ 郑颖人.库水作用下边坡稳定性分析［J］.岩土工程学报，2007，29（8）：1115－1121.（ZHENG Ying-ren.Stability Analysis of Slopes under Drawdown Condition of Reservoirs［J］.Chinese Journal of Geotechnical Engineering，2007，29（8）：1115－1121.（in Chinese））

［4］ 陈祖煜.土坡稳定性分析通用条分法及其改进［J］.岩土工程学报，1983，5（4）：11－27.（CHEN Zu-yu.The Generalized Method of Slices for Slope Stability Analysis and Its Modifications［J］.Chinese Journal of Geotechnical Engineering，1983，5（4）：11-27.（in Chinese））

［5］ SPENCER E.The Thrust Line Criterion in Embankment Stability Analysis［J］.Geotechnique，1973，23（1）：85－100.

［6］ 毛昶熙，段祥宝.渗流作用下的土坡圆弧滑动有限元计算［J］.岩土工程学报，2001，23（6）：746－752.（MAO Chang-xi，DUAN Xiang-bao.Finite Element Calculation on Circular Slip of Earth Slope under Seepage Action［J］.Chinese Journal of Geotechnical Engineering，2001，23（6）：746－752.（in Chinese））

［7］ 蔡正银.砂土的渐进破坏及其数值分析方法［C］／／2006年三峡库区地质灾害与岩土环境学术研讨会论文集.重庆：重庆大学，2006：72－81.（CAI Zhengyin.Gradual Failure and Numerical Analysis Method of Sand［C］／／Proceedings of the Special Topic Proseminar on Geologic Disasters in the Three Gorges ProjectRegion.Chongqing：Chongqing University，2006：72－81.（in Chinese））

［8］ 刘新喜.库水位下降对滑坡稳定性的影响及工程应用研究［D］.武汉：中国地质大学，2003.（LIU Xin-xi.Research on Landslide Stability in Drawdown of Reservoir Water Level and Its Application［D］.Wuhan：China U-niversity of Geosciences，2003.（in Chinese） ）

（编辑：周晓雁）

Seepage Stability of Upstream Slope of Earth Dam During the Drawdown of Reservoir W ater Level

ZHANG Da-wei1，YANWen-qun2
（1.Management Office of Lianyungang Shilianghe Reservoir，Lianyungang 222323，China；2.College of Hydraulic Science and Engineering，Yangzhou University，Yangzhou 225009，China）

When reservoirwater level drops sharply and rapidly from long-time high-level storage，the falling velocity of reservoir water level and soil property will exert adverse impact on the stability of upstream slope soilmass.The hazard of seepage on the upstream slope surface is demonstrated by seepage analysis softwares（Geoslope and unsst2）.Fitted curves between k／μv and critical descentaltitude of reservoir levelswhen flow with free surface does not appear are presented.Moreover，both the influence of soil anisotropy caused by various factors and the impact of substrate suction internal frictional angleφbon the stability of upstream slope seepage are also considered.The study reveals that all possible factors in practical projects and the results of seepage field calculation should be considered in the analysis of the seepage stability of upstream slope during the drawdown of reservoir level.

drawdown of reservoir water level；seepage stability；critical gradient of seepage from slope surface

P642

A

1001－5485（2011）07－0062－05

2010-08-02；

2011-04-14

张大伟（1984-），男，江苏东海人，助理工程师，硕士，主要从事岩土力学、水库管理等方面的工作，（电话）0518-86482070（电子信箱）daweiyz10＠163.com。