基于改进RBF神经网络的最大动剪切模量确定

陈志强，王亮清，刘顺昌，丰光亮

（中国地质大学工程学院，武汉 430074）

基于改进RBF神经网络的最大动剪切模量确定

陈志强，王亮清，刘顺昌，丰光亮

（中国地质大学工程学院，武汉 430074）

采用径向基函数（RBF）神经网络的手段，直接建立最大动剪切模量Gmax与孔隙比e、围压σ3、固结比kc这3个影响因素的非线性关系，避开了寻找Gmax与各影响因素之间定量经验公式的繁琐工作。通过模式搜索法计算出径向基函数的扩展速度的最优值，使模型的预测误差最小。以福建标准砂为例，模式搜索法得出的扩展速度SPREAD最优值为2.287，RBF网络预测的Gmax平均相对误差为0.931 6%，误差很小，说明RBF神经网络能方便、有效地确定不同条件下的Gmax，具有一定的推广利用价值。除了对Gmax能够很好地预测外，RBF网络对G-γ关系曲线也能很好地模拟。关 键 词：径向基神经网络；最大动剪切模量；Hardin公式；模式搜索法

1 概 述

土的动剪切模量是土体动力学特性的最重要参数之一［1－3］，同时也是土动力计算和场地地震安全性评价中不可或缺的内容。动剪切模量主要通过试验获得，通常分为现场测试和实验室测试2种，两者各有所长。对于土的非线性的情况，目前主要仍由室内试验测定［4］。确定动力学参数的仪器主要有：共振柱仪、扭剪仪、剪切仪、动三轴仪等。其中共振柱仪可直接测定在小应变范围内的动剪切模量，应用较普遍。

以式（1）双曲线模型对动剪切模量试验数据进行最小二乘法回归分析得到参数a和b。

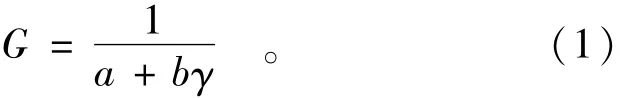
则最大动剪切模量

式中：G为动剪切模量；γ为动剪应变；a和b为拟合参数。

最大动剪切模量主要与孔隙比、围压、固结比等因素有关，但这些因素对最大动剪切模量的作用机理难以用数学表达式进行精确建模。Hardin和Black［1，2］给出平均主应力公式来计算固结比大于1.0时的最大动剪切模量，该公式中固结比对最大动剪切模量的影响不大。袁晓铭和孙静［5］对均等固结（kc＝1.0）时的最大动剪切模量G0m和kc＞1.0与kc＝1.0时最大动剪切模量的增量值ΔGm分别进行回归，即Gmax＝G0m＋ΔGm。在回归ΔGm时，使用最大动剪切模量的相对增量ΔGm／G0m，描述固结比kc在大于1.0时对最大动剪切模量的影响。这种方法虽然较Hardin公式有一定的改进，但过程繁琐，且将最大动剪切模量分成两部分来建模缺乏理论依据。

本文运用RBF神经网络的方法直接建立最大动剪切模量Gmax与孔隙比e、围压σ3、固结比kc的非线性关系，避开了寻找Gmax与各影响因素之间定量经验公式的繁琐工作。并通过模式搜索法计算出径向基函数扩展速度的最优值，使模型的预测误差最小。

另外，本文运用RBF网络对动剪切模量的非线性衰减情况也进行了预测。

2 确定最大动剪切模量的传统模型

Seed和Idriss［6］建立了砂土最大动剪切模量Gmax的经验公式：

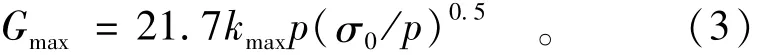
式中：kmax为土性参数；p为大气压力；σ0为有效平均主应力。式（3）较为简单，只考虑了有效平均主应力的影响。

Hardin和Black［1］给出适合各类土的最大动剪切模量Gmax经验表达式：

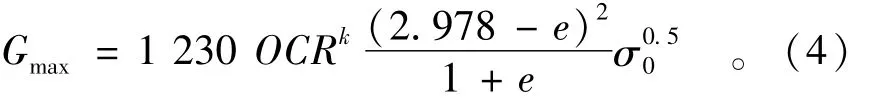
式中：σ0为有效平均主应力；OCR为超固结比；e为孔隙比。

袁晓铭、孙静［5］采用共振柱试验方法对Hardin公式进行了改进得到式（5），新公式对非等向固结下砂土最大动剪切模量的拟合相对式（4）有一定的改进。

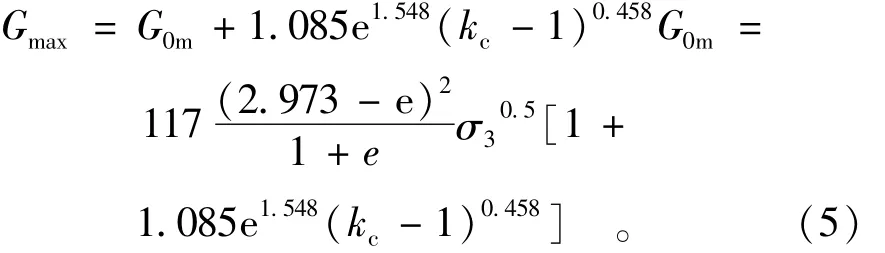
式（5）的建立过程为：先推导出计算均等固结下标准砂最大动剪切模量G0m的回归公式，该公式与Hardin公式在形式上完全一致，只是前面所选用的系数略有不同；再以幂函数模式建立非均等固结下最大动剪切模量相对于均等固结下最大动剪切模量的增量ΔGm／G0m和固结比的增量kc－1之间的关系。可见式（5）只针对固结比对最大动剪切模量的影响作了修正，孔隙比和围压的影响仍沿用Hardin公式的思想。

由于土体结构的复杂性，最大动剪切模量的影响因素较多，一些因素对最大动剪切模量的影响难以用简单的数学模型加以描述，而神经网络则可以通过对样本的反复学习来反映最大动剪切模量与各影响因素之间复杂的非线性关系。所以采用神经网络模型确定最大动剪切模量的方法应该优于传统方法。

3 径向基函数神经网络

3.1 径向基函数神经网络简介

由此可得隐含层第i个神经元的输入为

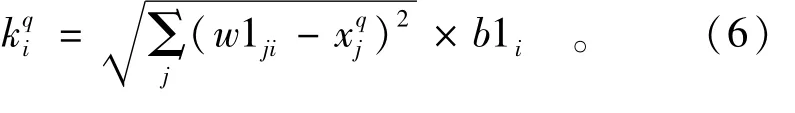
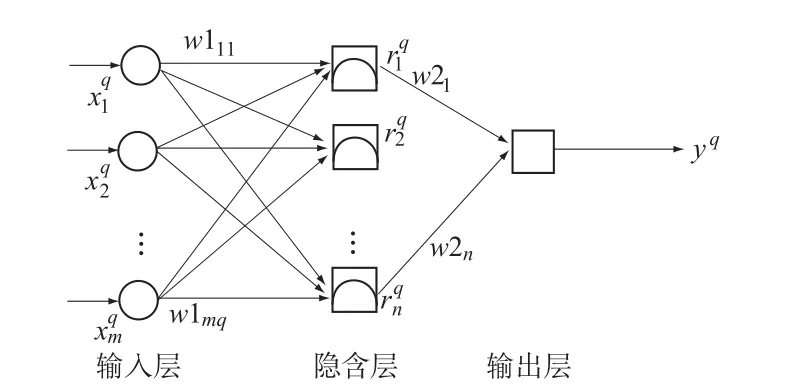
图1 RBF网络结构Fig.1 Structure of RBF Neural Network

输出为

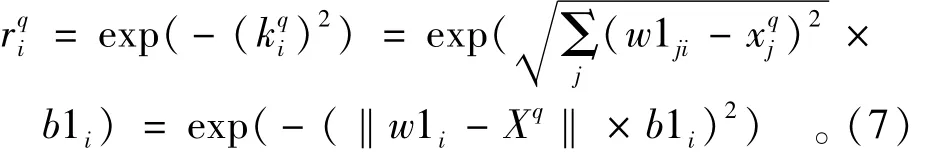
径向基函数的阈值b1可以调节函数的灵敏度，但实际工作中更常用另一参数C（称为扩展常数）。b1和C有一定的关系，本文取b1i＝0.832 6／Ci。

输入层的输入为各隐含层神经元输出的加权求和。由于激励函数为纯线性函数，因此输出为

3.2 径向基函数神经网络的MATLAB实现

MATLAB神经网络工具箱为径向基网络提供了许多工具箱函数，其中newrbe函数是一个用于设计准确径向基网路的函数。调用格式为

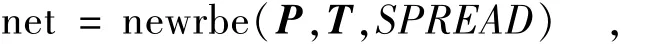
其中：P为Q组输入向量组成的R×Q维矩阵；T为Q组目标向量组成的S×Q维矩阵；SPREAD为径向基函数的扩展速度，默认为1；SPREAD越大，函数拟合就越光滑。但是过大的SPREAD意味着需要非常多的神经元以适应函数的快速变化。如果SPREAD设得过小，则意味着需要许多神经元来适应函数的缓慢变化，这样一来，设计的网络性能就不会很好。因此，在网络的设计过程中，选择一个合适的SPREAD很关键。本文将使用模式搜索法寻找出最优SPREAD值。

利用函数newrbe创建一个精确的神经网络，该函数在创建RBF网络时，自动选择隐函层的数目，对于给定的训练向量能够生成一个零误差的网络对象。

径向基传递函数为radbas函数。该函数原型为y＝exp（－x2）。

悄寂的山坳，悄寂的坟地，周边一个人影儿也没有，只有不会说话的高天白云一脸坏笑的窥测，以及荆棘绿草满含讥讽的睨视。如此好的保密条件，足足可以帮助三喜实现这一小小的阴谋。他因喜不自禁而抓耳挠腮，下定了决心就照此办理！

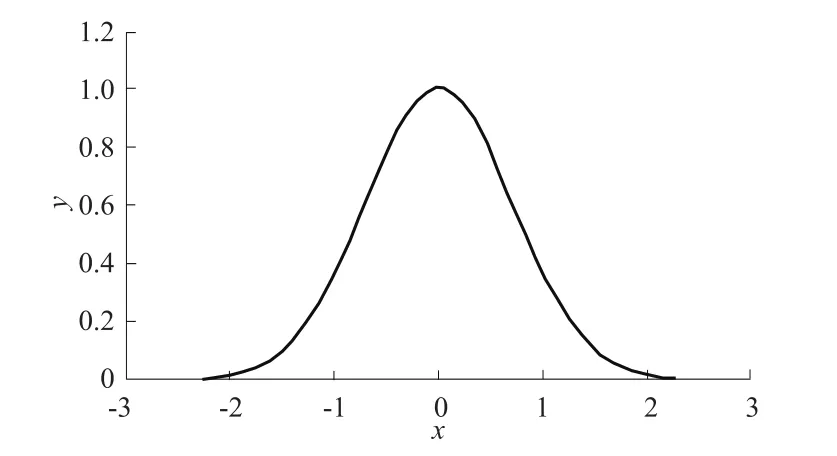
图3 径向基传递函数radbasFig.3 Radbas－the transfer function of RBF Neural Network

3.3 RBF神经网络相对于BP网络的优点

BP神经网络是一种常用的全局逼近神经网络，从理论上讲，3层BP网络就可以实现从输入到输出的任意函数映射。但是由于BP神经网络是基于梯度下降的误差反向传播算法进行学习的，且在训练过程中需要对网络的所有权值和阈值进行修正，所以网络的学习速度较慢，而且很容易陷入局部最小点，易产生振荡，无法保证每次训练时BP算法的收敛性和全局最优性。

与BP神经网络相比，RBF网络是一种局部逼近网络，对于每个训练样本，它只需要对少量的权值和阈值进行修正，所以RBF神经网络不仅学习速度快，而且避免了局部最小问题，同时，由于只有少量的权值需要调整，其推广能力显著增强，使得其对新样本的预测能力显著增强。因此，RBF神经网络在逼近能力、分类能力和学习速度等方面均优于BP神经网络［8－9］。故本文采用RBF神经网络进行预测。

4 模式搜索法

与遗传算法一样，模式搜索法也可以用来寻找最优解。与使用梯度或高阶导数信息来搜索优化点的较传统的优化算法相反，模式搜索法不要求任何目标函数梯度的信息。模式搜索算法搜索当前点周围的一系列点，寻找出目标函数值低于当前点值的点，并将该点作为下一次迭代的当前点。它可以处理边界约束、线性等式、线性不等式，并且不需要目标函数可微或连续［10］。

本文定义目标函数F：

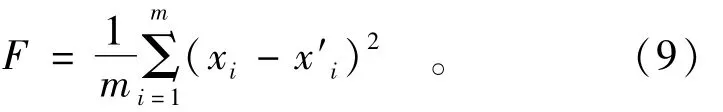
式中：m为预测数据组数；xi为第i组真实值；x′i为其对应的预测值。

本文计算最优SPREAD的具体步骤为：①确定一个初始点X0；②通过RBF神经网络计算出初始点的目标函数值F（X0），然后按同样方法计算其相邻的其它各点的值F（X0＋V（j）L），j∈（1，2，…，2N），L默认为1，因为只有一个自变量，则N＝1，V＝［－1；1］；③如果X0相邻点中有一点的函数值比F（X0）更优则表示搜索成功，那么X1＝X0＋V（j）L，且下次搜索时以X1为中心，以L＝L×2为步长，若没有找到这样的点则表示搜索失败，返回仍以X0为中心，以L＝L×0.5为步长搜索；④重复②③的操作直到满足终止条件为止，终止条件可以是迭代次数已到设定值或者误差小于规定值等，最终得到的Xk即为最优SPREAD（k为成功搜索的次数）。

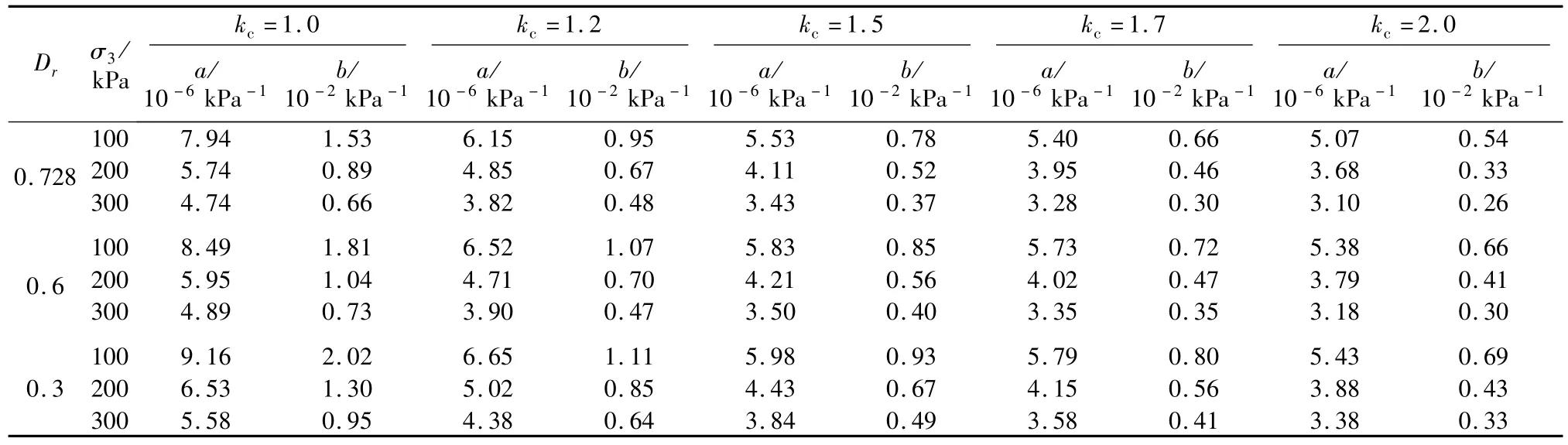
表1 标准砂在不同条件下G-γ关系曲线参数a，b值［4］Table 1 Parameter values of G-γrelation curve of standard sand in different conditions

5 标准砂最大动剪切模量预测

孙静等［4］采用筛选后的福建标准砂进行试验。试验用砂的主要技术指标如下：土粒密度ρs为2.66 g／cm3；最大干密度ρdmax为1.686 g／cm3；最小干密度ρdmin为1.481 g／cm3；最大孔隙比emax为0.796；最小孔隙比emin为0.578；不均匀系数Cu为1.64，曲率系数Cc为0.85。属于级配良好的中砂。

采用3种不同相对密度的标准砂进行偏压试验，对同一种相对密度的标准砂，施加3种不同围压，每一种围压下，施加5种不同的偏压进行试验，在共振柱上测出相应的动剪切模量，得到45种工况下不同相对密度、不同围压和不同固结比的动剪切模量与剪应变的试验关系。根据式（1）对测得的动剪切模量试验点进行分析，可以得到每种工况下的拟合参数a，b值，如表1所示。根据a值和式（2）可得到每种工况下最大动剪切模量值，如表2所示。

相对密度和孔隙比存在的转换关系如式（10）所示：

故相对密度为0.728，0.6，0.3对应的孔隙比分别是0.637 296，0.665 2，0.730 6。

如果将孔隙比、围压、固结比作为一组输入向量，将对应的最大动剪切模量值作为目标向量时，可将表2中数据构造成45组向量，如表3所示。

将序号为奇数的数据作为训练样本，其中前面3列数据作为输入向量P，最后1列作为目标向量T，将序号为偶数的数据作为测试样本，检查网络的预测精度。

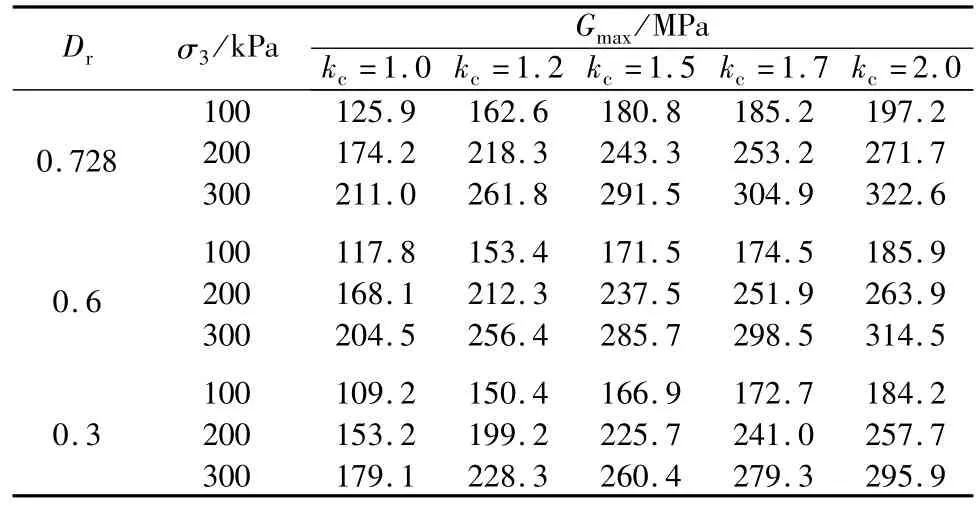
表2 标准砂在不同条件下最大动剪切模量值Table 2 Themaximum dynam ic shear modulus of standard sand in different conditions

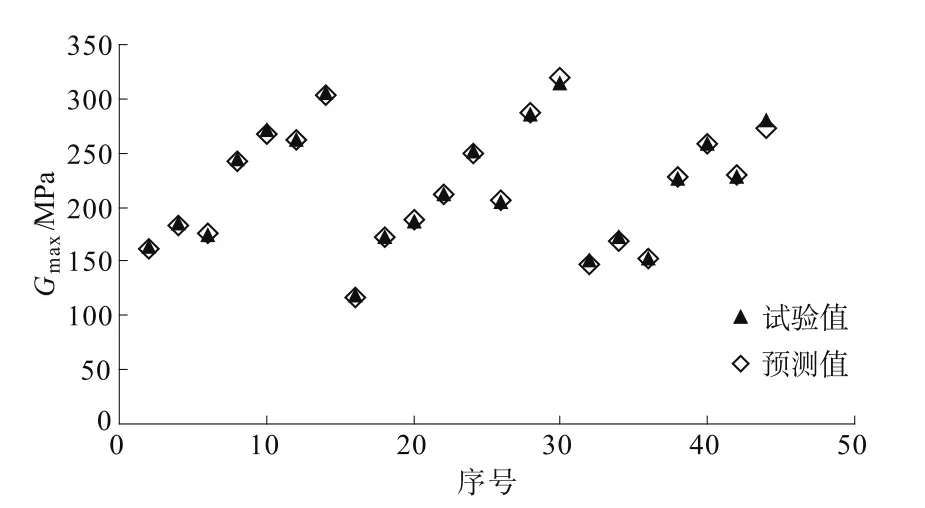
图4 RBF神经网络预测效果图Fig.4 Prediction results by RBF Neural Network

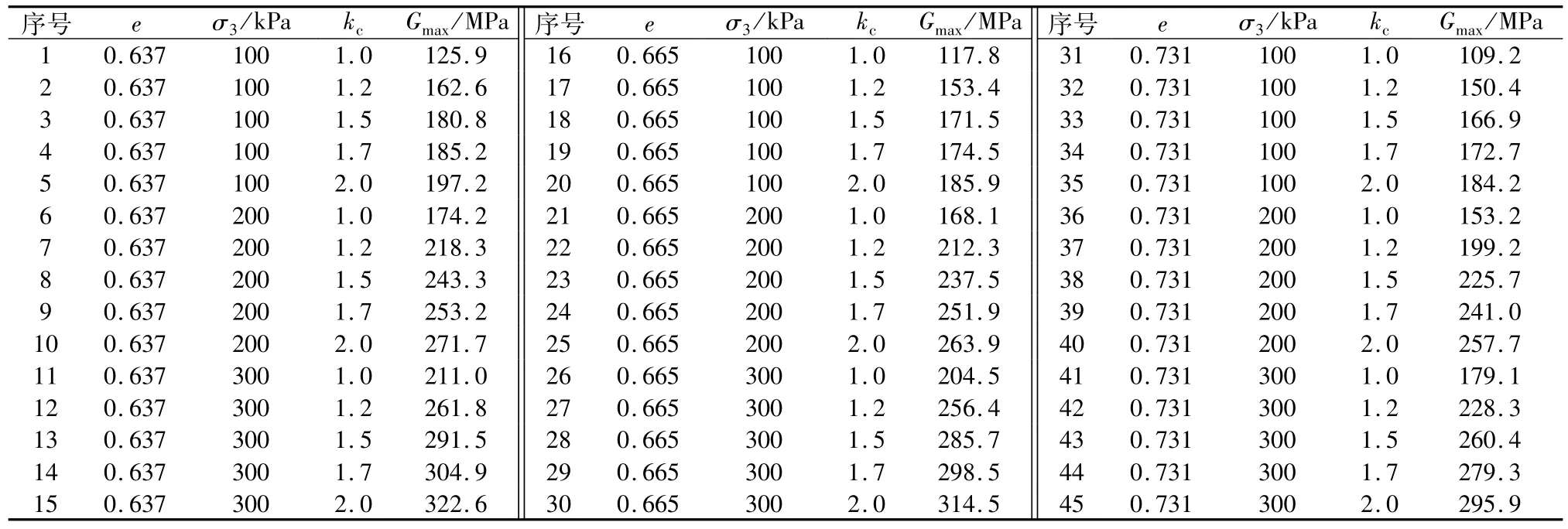
表3 RBF神经网络训练及测试样本Table 3 Training sam ples and test samples of RBF Neural Network

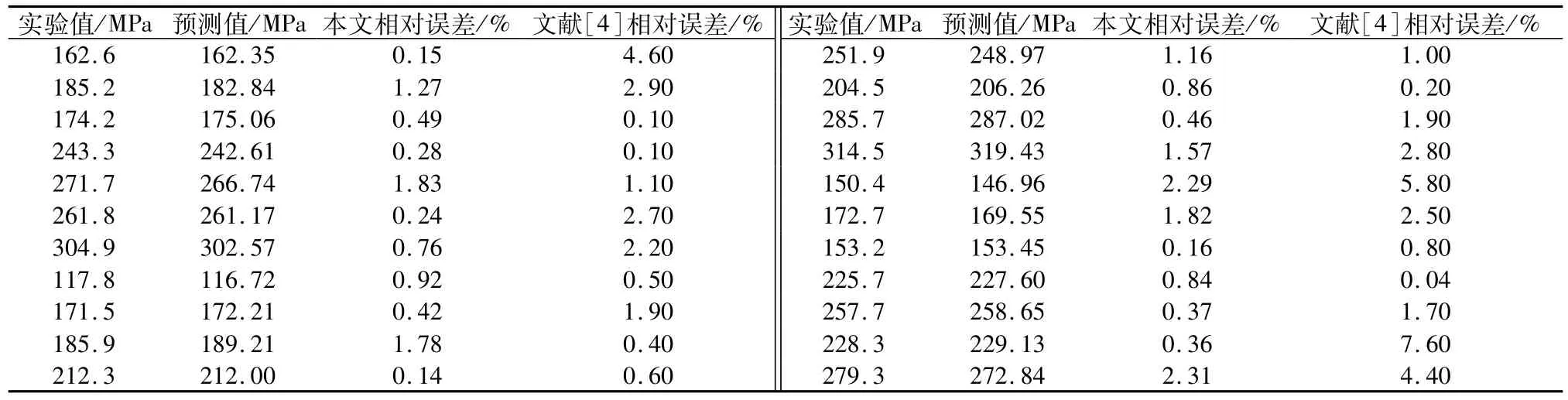
表4 RBF神经网络预测与文献［4］误差对比Table 4 The error com parison between the forecast of RBF Neural Network and the forecast in reference［4］

经模式搜索法得出最优SPREAD＝2.287。此时目标函数值为7.108 8，RBF网络预测的预测结果如图4和表4所示。

由图4和表4可知，基于RBF神经网络的预测方法预测误差很小，相对误差最大值为2.31%，而文献［4］的相对误差最大值为7.60%。经计算，文献［4］的平均相对误差为2.083 6%，而本文预测结果的平均相对误差为0.931 6%。可见RBF神经网络预测不同条件下最大动剪切模量的优越性。

6 标准砂模量比曲线预测

同样的，将孔隙比、围压、固结比作为一组输入向量，将对应的非线性关系曲线参数a，b值作为目标向量时，可将表1中数据构造成45组向量。与前面建立最大动剪切模量预测网络的方法相同，只不过将目标向量改为a和b。

经模式搜索法得出的最优SPREAD＝0.653，RBF神经网络预测结果如表5所示。

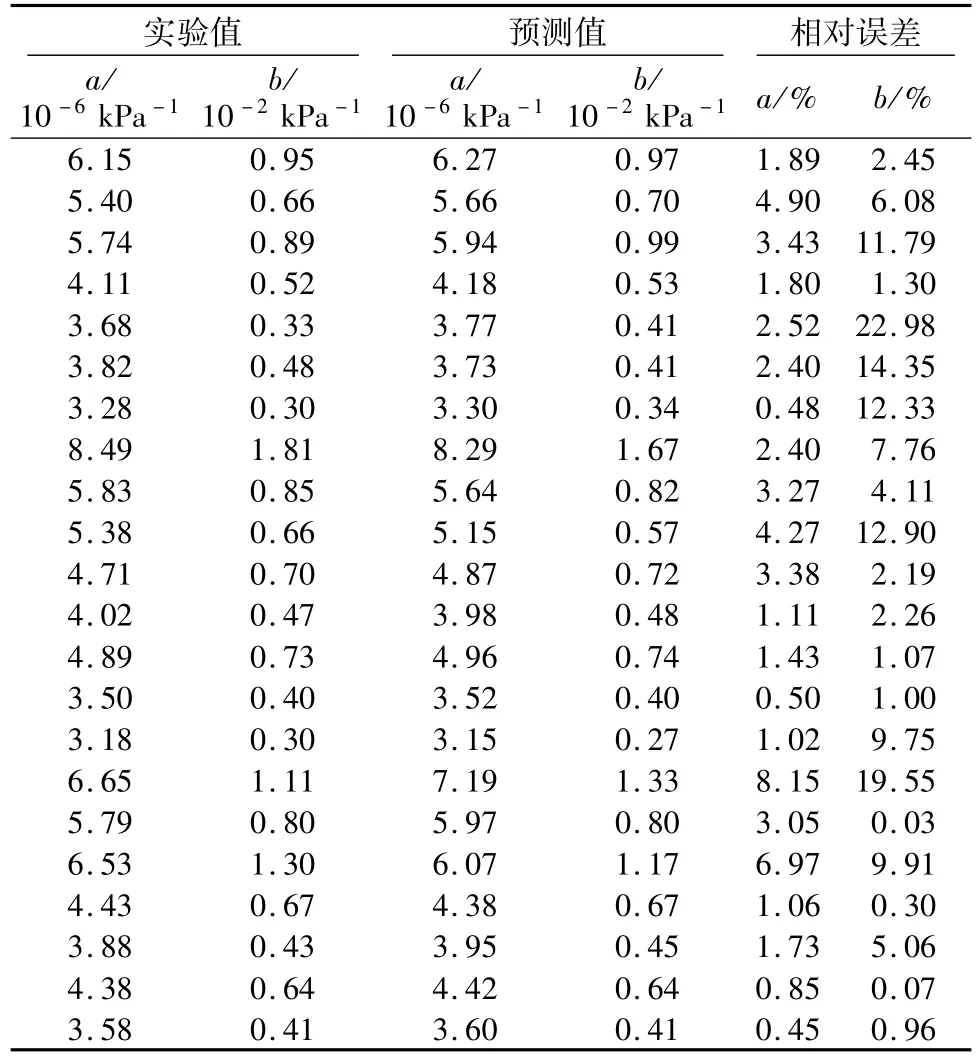
表5 RBF神经网络对非线性参数预测情况Table 5 The p rediction of non linear parameters by RBF Neural Network

由表5可知，网络对a值的预测误差普遍偏小，对b值的预测误差局部偏大而总体较小。经计算，a值的平均相对误差为2.593 3%，b值的平均相对误差为6.736 7%，可见RBF神经网络还可以较好地模拟不同固结比、围压、孔隙比条件下的动剪切模量比与剪应变非线性关系。

7 结 语

由于土体的复杂性与混沌性质，经验公式不可能完全反应动剪切模量的变化规律。某些影响因素与最大动剪切模量的非线性关系非常复杂，它们之间不能用简单的基本函数表示。另外，经验公式中各变量之间的关系是相互独立的，而事实上他们可能是相关联的。例如围压和固结比都会对孔隙比造成一定的影响。所以在影响因素比较多时，确定最大动剪切模量的公式会非常复杂，且不一定准确。

而神经网络具有原则上容错、结构拓扑鲁棒、联想、推测、记忆、自适应、自学习、并行和处理复杂模式的功能，人工神经网络可以通过对一组样本的反复学习，反应一个非常复杂的映射关系，从而避免了繁琐的公式推导。采用模式搜索方法对RBF网络结构进行优化，方法简单，效果显著。以福建标准砂为例，说明改进的RBF神经网络不仅对最大动剪切模量能很好地预测，对动剪切模量与动剪应变关系曲线也能很好地模拟。

另外，采用改进RBF神经网络的方法代替传统的数学公式方法对最大动剪切模量的确定不仅适用于砂土，还可以推广至其它性质土的最大动剪切模量的确定，具有一定的推广应用价值。

［1］ HARDIN B O，BLACKW L.Vibration Modulus of Normally Consolidated Clay［J］.SoilMechanics and Foundations Division，ASCE，1968，94（2）：353－369.

［2］ HARDIN B O，BLACKW L.Vibration Modulus of Normally Consolidated Clay（Closure）［J］.Soil Mechanics and Foundations Division，ASCE，1969，95（6）：1531－1537.

［3］ SEED H B，WONG R T，IDRISS IM，et al.Modulus and Damping Factors for Dynamic Analysis of Cohesionless Soils［J］.Geotechnical Engineering，ASCE，1986，112（11）：1016－1032.

［4］ 孙 静.岩土动力学参数测试技术与应用［M］.哈尔滨：黑龙江大学出版社，2007.（SUN Jing.Soil Testing Technology and Application of Dynamic Parameters［M］.Harbin：Heilongjiang University Press，2007.（in Chinese））

［5］ 袁晓铭，孙静.非等向固结下砂土最大动剪切模量增长模式及Hardin公式修正［J］.岩土工程学报，2005，27（3）：264－269.（YUAN Xiao-ming，SUN Jing.Model of Maximum Dynamic Shear Modulus of Sand under Anisotropic Consolidation and Revision of Hardin’s Formula［J］.Chinese Journal of Geotechnical Engineering，2005，27（3）：264－269.（in Chinese））

［6］ SEED H B，IDRISS IM.Soil Moduli and Damping Factors for Dynamic Response Analysis，Report No.EERC 70－10［R］.Berkeley：Earthquake Engineering Research Center，University of California，1970.

［7］ 葛哲学，孙志强.神经网络理论与MATLAB2007实现［M］.北京：电子工业出版社，2007.（GE Zhe-xue，SUN Zhi-qiang.Neural Network Theory and Its ApplicationUsing MATLAB 2007［M］.Beijing：Electronic Industry Press，2007.（in Chinese））

［8］ 沈 强，陈从新，汪 稔.边坡位移预测的RBF神经网络方法［J］.岩石力学与工程学报，2006，（S1）：2882－2887.（SHEN Qiang，CHEN Cong-xin，WANG Ren.Method to Forecast Displacement of Slope Based on RBF Neural Network［J］.Chinese Journal of Rock Mechanics and Engineering，2006，（S1）：2882－2887.（in Chinese））

［9］ 李 红，彭 涛.基于BP、RBF神经网络混凝土抗压强度预测［J］.武汉理工大学学报，2009，31（8）：33－36.（LIHong，PENG Tao.Prediction of Concrete Compression Strength Based on BP and RBF Neural Network Theories［J］.Journal of Wuhan University of Technology，2009，31（8）：33－36.（in Chinese））

［10］雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及运用［M］.西安：西安电子科技大学出版社，2005.（LEI Ying-jie，ZHANG Shan-wen，LI Xu-wu，et al.MATLABGA Toolbox and Application［M］.Xi’an：Xidian University Press，2005.（in Chinese） ）

（编辑：王 慰）

Determ ination of the M aximum Dynam ic Shear M odulus Based on Improved RBF Neural Network

CHEN Zhi-qiang，WANG Liang-qing，LIU Shun-chang，FENG Guang-liang
（Faculty of Engineering，China University of Geo-sciences，Wuhan 430074，China）

To avoid the complicated work of searching for quantitative experiential formula，a nonlinear relationship betweenmaximum dynamic shearmodulus（Gmax）and the influence factors including void ratio（e），cell pressure（σ3），and consolidation ratio（kc）was built directly by using Radial Basis Function（RBF）neural network.In addition，the optimal value of spread speed（SPREAD）of RBF was calculated by pattern search method tominimize the prediction error.Taking standard sand in Fujian province as an example，the optimal value of SPREAD calculated by pattern searchmethod equals to 2.287，and the average relative error of Gmaxpredicted by RBF neural network is0.931 6%，which is quite small.It shows that RBF neural network can determine Gmaxunder different conditions conveniently and effectively.Besides，the relationship curve of G-γcan also be simulated by this network.Therefore，themethod of using RBF neural network to calculate themaximum dynamic shearmodulus is recommended to be used widely.

radial basis function neural network；maximum dynamic shear modulus；Hardin formula；pattern search method

TP183

A

1001－5485（2011）07－0051－06

2010-07-15

陈志强（1987-），男，四川绵阳人，硕士研究生，主要从事岩土体工程性质及边坡稳定性分析方面的研究，（电话）15927189793（电子信箱）cug50061＠163.com。