基于MMMA的双模式变步长盲均衡算法

王晓东，孟玲玲，韩宝如

（1.燕山大学 信息学院，河北 秦皇岛 066004；2.海南软件职业技术学院 电子工程系，海南 琼海 571400）

责任编辑:许 盈

0 引言

数字无线通信系统中信号会因为多径衰落而在接收端产生严重的码间干扰，因此在实践中经常会用均衡技术来消除码间干扰。恒模算法（CMA）是实际应用中最为普遍的算法，该算法利用信号模值的统计特性进行均衡，因为其稳健性良好、计算复杂度低等特点而得到了广泛应用。但是该算法虽能实现盲均衡效果，但是它有收敛速度慢、剩余误差大、相位模糊等不足[1]。文献[2]在恒模算法的基础上提出了一种修正恒模算法（MCMA），从根本上解决了相位旋转问题,但是该算法在收敛速度和剩余误差方面没有明显的改善。文献[3]在文献[2]的基础上提出MCMA+DD－LMS的方法，不仅解决了CMA的相位偏转问题，而且在收敛速度和剩余误差方面也有很多改进。上述文献中提出的方法都是采用固定步长，文献[4]提出了VS－MCMA+DD－LMS方法，改固定步长为变步长，这样可以有效地减小剩余误差，提高收敛速度。笔者在此基础上，以MMMA算法为核心，结合DD－LMS算法和变步长算法，比文献[4]算法减小了剩余误差，引入解相关处理，进一步提高了收敛速度。

1 算法描述

1.1 常见的盲均衡算法

设a（n）是原始发送序列，h（n）是信道的冲激响应，v（n）是信道中加性噪声，X（n）是经信道加噪后的信号，w（n）是采用抽头延迟线模型的线性均衡器，Y（n）是均衡后的信号，e（n）代表迭代误差。

在CMA中，误差函数定义为

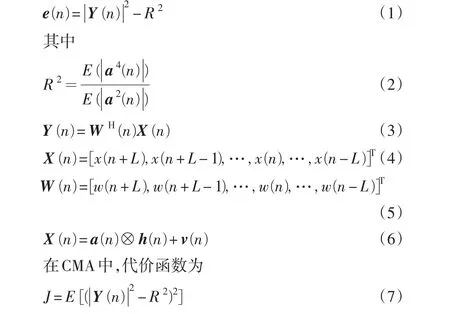
均衡器权向量的迭代过程为

式中:μ是步进长度。

可以看出，CMA的误差函数仅包含信号的幅度信息，这样就导致不能克服信道引起的相位误差。文献[2]中提出分别对信号的实部和虚部进行均衡的MCMA算法，在均衡的过程中既包含了信号的幅度信息又包含了相位信息，从而可以补偿信道引起的相位偏转。该算法误差函数的实部和虚部分别为

DD－LMS的误差控制函数为

式中:Y1(n)是判决输出值。

抽头系数递推公式为

DD－LMS算法具有计算简单，收敛速度快，剩余误差小的优点，但是在判决错误率较高的时候，算法可能无法收敛。

DD－LMS算法比较典型的应用是由其他收敛能力较好的盲均衡算法做冷启动，当剩余误差降低到一定的程度时切换到DD－LMS算法。文献[3]中提出MCMA算法和DD－LMS算法相结合，充分利用了两种算法的优点。

自适应均衡器的收敛速度在很大程度上都取决于步进长度μ，当步进长度较大时，均衡器收敛速度快，步进长度较小时收敛速度慢，但是剩余误差会随着步进长度的变大而变大。变步长算法可以有效解决这一矛盾，在开始阶段使用较大的步长因子加快收敛速度，随着迭代次数增加，当均衡逐渐接近最优时步长因子也会随之减小，因此减小了剩余误差。在文献[4]中提出VS－MCMA+DD－LMS算法，利用了变步长算法的优点。

1.2 新算法描述

1.2.1 VS－MMMA+DD－LMS算法

由于CMA算法和MCMA算法中代价函数中模值都是恒定的，导致均衡器的抽头趋势都是使均衡器输出的数据向半径为的圆上靠近，对于非常模信号（如QAM信号），即使在算法收敛时也会存在较大的剩余误差。多模算法（MMA）[5]用均衡器输出的判决值来代替常模算法中的R，使均衡器输出与多个模相吻合，算法收敛后误差函数趋于零，减小剩余误差。该算法的误差函数为

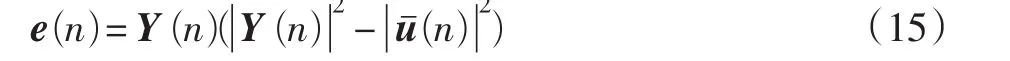
抽头递推公式为

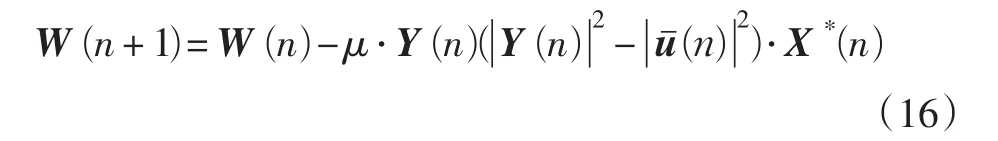
同样可以发现，MMA算法也存在相位偏转的问题，类似于MCMA对CMA的修正，MMMA算法分别对信号的实部和虚部进行均衡，使得信号在均衡过程中包含了相位信息，有效克服了信号的相位偏转。该算法误差函数的实部和虚部分别为

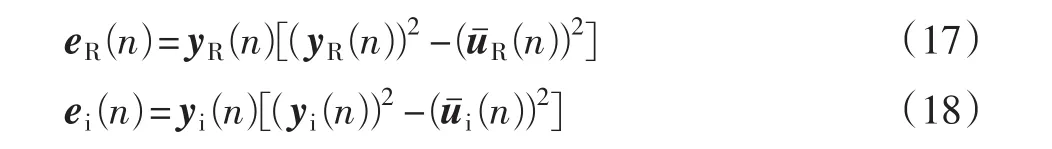
抽头系数递推公式为

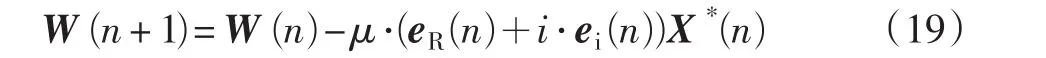
从以上分析可知，对于非常模信号，MMMA算法的均衡性能要优于MCMA，所以笔者对VS－MCMA+DD－LMS算法进行了改进，提出VS－MMMA+DD－LMS算法。

为了提高收敛速度，采用指数型变步长公式[6]

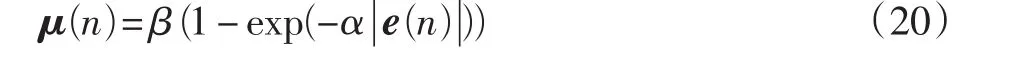
式中:α，β为参数，α用来控制曲线的形状，β用来控制曲线的取值范围，通过调节α和β的值来改善算法的收敛速度。

VS－MMMA+DD－LMS算法的切换准则为:设定误差判决值γ，开始阶段采用VS－MMMA算法进行均衡，当剩余误差小于判决值时自动切换到DD－LMS算法进行均衡。γ值的设定根据均衡器输入端的信噪比来确定，设输入的信噪比为SNR[4]，则有

式中:E2s是信号功率，σ2噪声功率，由此可得

判决值γ〈σ，经过多次试验确定判决值的最优值。

1.2.2 VS－UMMMA+DD－LMS算法

MMMA算法中，输入信号高度相关时会影响均衡的收敛速度。针对此不足，对MMMA算法做了进一步改进，提出UMMMA算法，即对输入信号进行解相关处理，使得输入信号尽可能保持独立，这样可以进一步提高均衡的收敛速度。

定义X（n）与X（n-1）在n时刻的相关系数为[7]

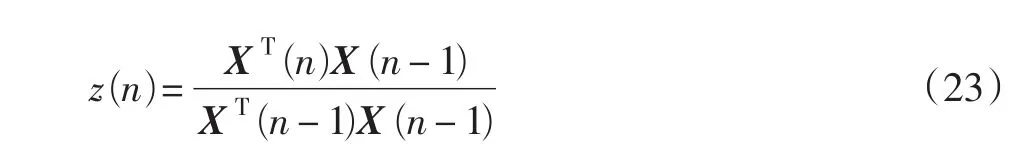
若z（n）=0，则称X（n）与X（n－1）不相关；当0〈z（n）〈1时，称X（n）与X（n－1）相关，并且z（n）越大，它们之间的相关性越大。显然z（n）X（n－1）代表了X（n）中与X（n－1）相关的部分，若从X（n）中减去该部分，则这一减法运算就相当于解相关，现在用解相关的结果作为更新方向向量V（n）

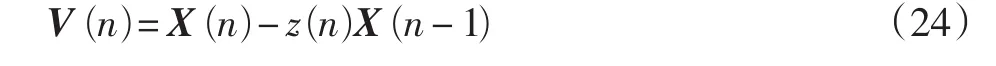
该算法的抽头递推公式为

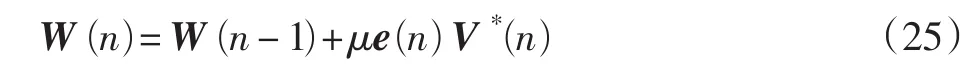
式中:误差函数e（n）同MMMA算法。

上述分析可知，UMMMA均衡性能要优于MMMA均衡，所以笔者又提出VS－UMMMA+DD－LMS算法，新算法在均衡过程中的切换准则同VS－MMMA+DD－LMS算法。

2 仿真结果分析

对未经过处理的数字信号，以及经过CMA均衡、新算法均衡后信号的星座图进行了仿真，对文献[3]中提出的VS－MCMA+DD－LMS算法、文中提出的VS－MMMA+DDLMS算法和VS－UMMMA+DDLMS算法的剩余误差进行了仿真，并对仿真结果进行了对比分析。文中以常用的数字信号16QAM作为处理信号，以信道条件比较恶劣的数字无线信道作为传输信道，信道响应为h=[－0.005－0.004j，0.009+0.030j，－0.024－0.104j，0.854+0.520j，－0.218+0.273j，0.049－0.074j，－0.016+0.020j]，抽头系数取11，DD－LMS迭代步进长度为0.05，变步长因子α=10，β=0.016，判决值设定为0.08，当信噪比SNR=10 dB时仿真的结果如图1～图4所示。

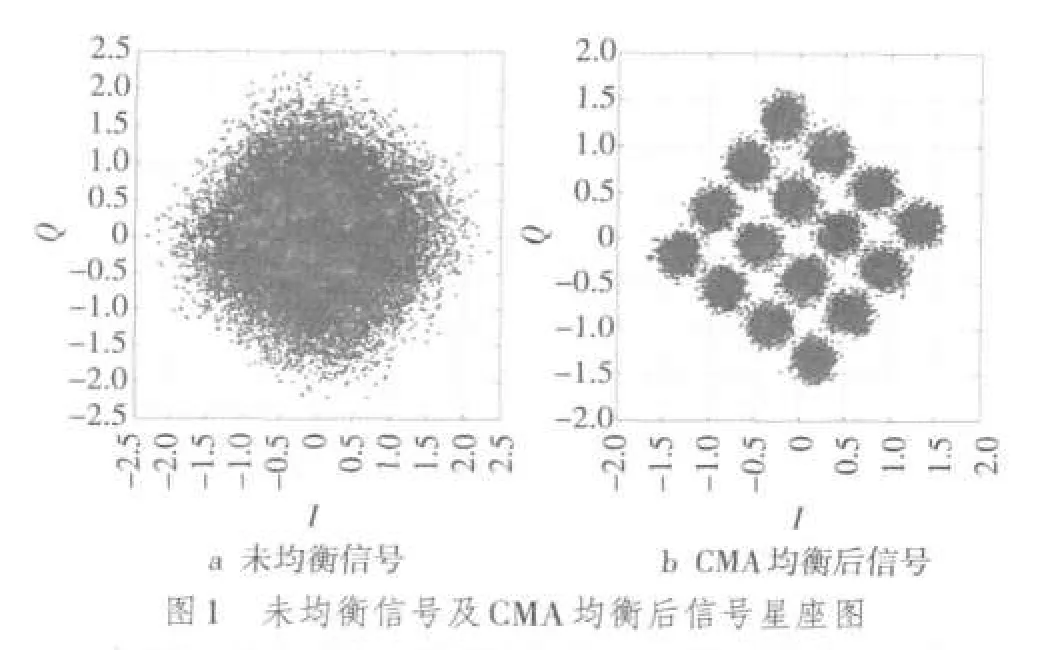
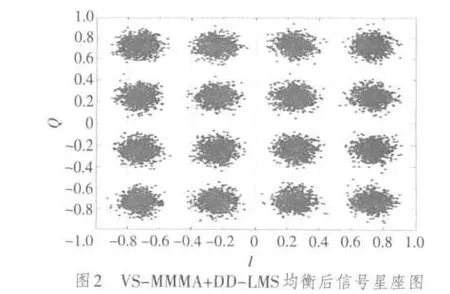
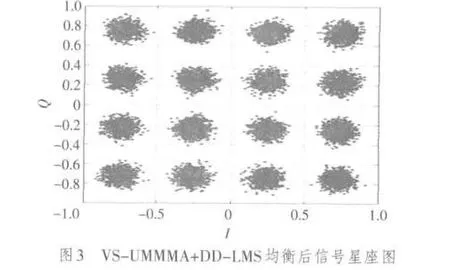
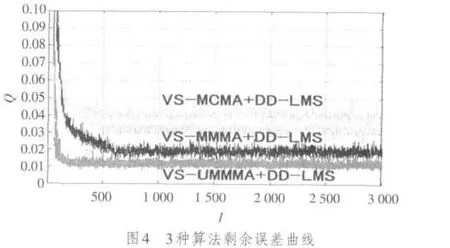
由图1对比可知，信号经过CMA算法均衡后，信号在信道传输过程中产生的相位偏转无法修正。图2、图3为接收信号经提出的两种算法均衡后的信号星座图，从图中可以看出，新算法可以有效地修正接收信号的相位偏转。图 4是 VS－MCMA+DD－LMS算法、VS－MMMA+DD－LMS算法和VS－UMMMA+DD－LMS算法的剩余误差比较，从图中看出VS－MMMA+DD－LMS算法与VS－MC⁃MA+DD－LMS算法的收敛速度相当，但是VS－MMMA+DD－LMS算法收敛后的剩余误差要小于VS－MCMA+DD－LMS算法，VS－UMMMA+DD－LMS算法收敛后的剩余误差和VS－MMMA+DD－LMS算法接近，但是收敛的速度有明显的改进。

3 小结

提出了SV－MMMA+DD－LMS，VS－UMMMA+DD－LMS这两种新的盲均衡算法，两种算法既能有效克服数字接收信号存在的相位偏转，同时在剩余误差和收敛的速度方面也有明显的改进。仿真结果表明该算法具有较好的性能，有一定的参考使用价值。

[1]孙兰清，葛临东，刘锋.常模类盲均衡算法的研究[J].电视技术，2006，30（10）:12－14.

[2]ENDRESTJ.Equalizing with fractionally space constant modulus and second orderstatistics blind receiver[D].Ithaca，N Y:CornellUniversity，1997.

[3]朱行涛，刘郁林，敖卫东.一种基于MCMA的双模切换变步长盲均衡算法[J].重庆邮电学院学报，2006，18（6）:689－692.

[4]杨斌，郭黎利，吴浩江.一种变步长双模式盲均衡算法的研究[J].信息技术，2009（2）:89－91.

[5]李昌斌，徐昌庆.修正多模算法的盲信道均衡[J].信息技术，2004（10）:16－18.

[6]段正华，王梓展，鲁薇.一种改进的解相关LMS自适应算法[J].湖南大学学报，2006，33（3）:114－118.

[7]孙丽君，孙超.几种适用于水声信道的常模类盲均衡算法研究[J].电声技术，2005，29（1）:7－8.