改进Verhulst模型与灰色效果测度的软岩巷道顶板破坏规律分析

陈建宏，郑海力，施飞，杨瑞波，蒋权

(中南大学 资源与安全工程学院 湖南省深部金属矿产开发与灾害控制重点实验室，湖南 长沙，410083)

在软岩巷道破坏的众多方式中，顶板沉降位移过大是最常见的破坏方式之一。由于顶板承受的地应力过大、顶板岩体质量太差、巷道跨度过大以及支护方式不合理等都会导致顶板位移过大而使得巷道破坏。软岩巷道顶板位移的影响因素是繁多而复杂的，而且各影响因素对位移的影响至今尚没有合理的计算公式来进行计算，因此，对软岩巷道顶板位移影响因素的选取并根据这些因素判定软岩巷道顶板位移以及最终破坏方式比较困难[1−5]。改进 Verhulst 模型[6−7]与灰色效果测度则可以很好地解决这些问题。改进 Verhulst模型可以根据软岩巷道顶板位移的早期观测值而预测出巷道顶板位移的最终值，根据最终位移判断巷道是否被破坏。相对于传统的Verhulst模型，改进Verhulst模型的预测结果具有更高的精度，预测结果更加准确、可靠。对于软岩巷道顶板位移预测出现微小偏差便有可能酿成事故的情况，预测结果的准确性是至关重要的。为此，本文作者根据矿山实际情况，选取软岩巷道顶板位移的影响因素，对这些影响因素与软岩巷道位移以及是否破坏的关系，利用灰色效果测度理论对这些因素进行效果测度，并利用相对重要程度相关等级计算法确定这些因素对巷道位移影响的权重，最终对这些因素对软岩巷道顶板的影响进行综合测量。灰色效果测度适合于对不同量纲、不同含义的量综合效果进行测量。将灰色效果综合测度值与软岩巷道顶板位移最终值以及巷道破坏方式对应，得出与灰色综合效果测度值对应的巷道顶板稳定性分析结果，以便为矿山提前应对巷道顶板破坏、开展合理的二次支护工作提供依据。

1 系统建模

1.1 影响因素的选取

影响软岩巷道顶板位移的因素繁多而又复杂，目前仍没有形成统一的选取标准，但归结起来无非是外部因素与自身因素。外部因素通过外界媒介影响软岩巷道顶板位移，内部因素因为巷道自身条件而影响软岩巷道的位移。结合矿山的具体实际情况，本模型选取地应力、围岩质量、巷道跨度与支护方式作为软岩巷道顶板位移的影响因素，见图1。

1.2 最终位移的预测

选取一批具有代表性的巷道，在其顶板安装位移应变片，对巷道顶板的位移进行观测统计。很显然，顶板的位移有一个从不稳定到稳定的过程，最初的位移较大，后来，巷道顶板应力重新分布，趋于稳定，位移越来越小，即观测值的原始数据变化规律近似为“S”形。要对这种曲线的观测值进行预测，应使用Verhulst模型。这里使用比传统的Verhulst模型预测精度更高的改进Verhulst模型对最终位移进行预测。

设巷道位移初期观测值为(1)X=

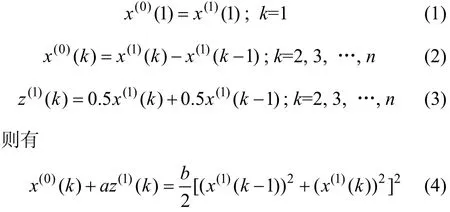
式(4)即为改进Verhulst模型。其中，利用最小二乘法得出的为差分Verhulst模型的参数列。

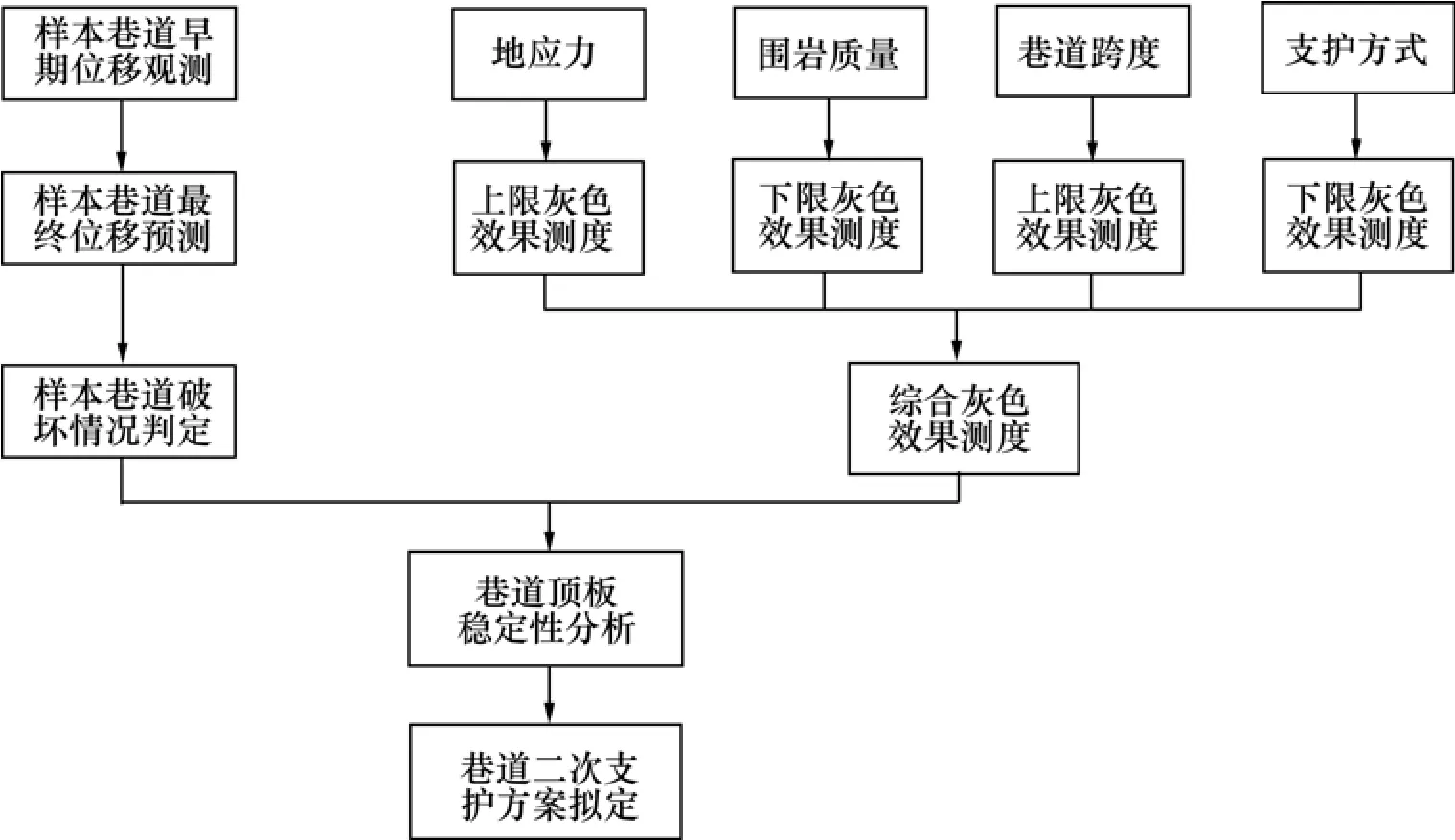
图1 系统建模流程图Fig.1 Flowchart of system model

若有矩阵：

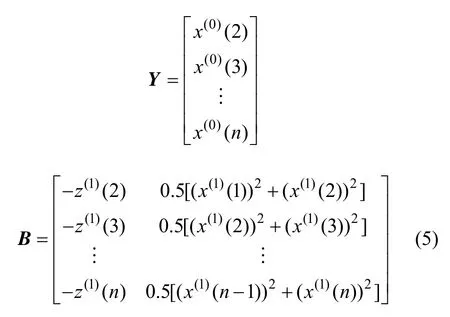
则改进Verhulst模型的最小二乘估计参数列为：

改进Verhulst模型的影子方程为：

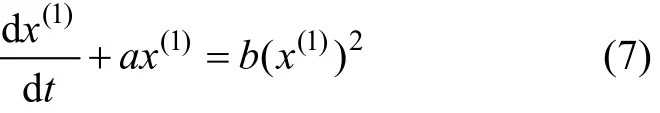
影子方程的解即时间响应函数为：

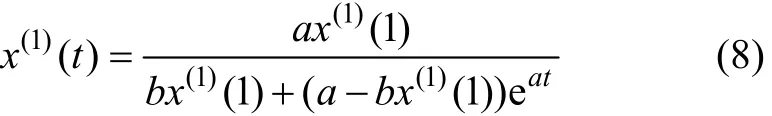
改进Verhulst模型的时间响应序列为：

式中：k=1, 2, …,n。

建立改进Verhulst模型后对式(9)进行误差检验，包括残差检验、相对误差检验、后验差检验以及后验比值检验[8]。只有当误差检验均合格时，模型的精度才被认为是合格的，可以用于对巷道最终位移进行预测。当模型的精度不高时，可对原模型进行修正，以提高精度。误差检验等级如表1所示。

检验合格后即可利用其时间响应序列对巷道顶板最终位移进行预测。由于巷道顶板位移在后期仍然慢慢变大，因此，当巷道顶板位移预测值在一个极小的区间范围内变化时，便可忽略其对巷道位移的影响，判定其为最终位移。

表1 灰色预测模型精度检验等级Table1 Precision inspection level of grey forecasting model

1.3 影响因素效果测度

在选取的影响软岩巷道顶板位移的因素中，地应力与巷道跨度越大，巷道顶板位移也就越大，因此，对这2项指标采用上限效果测度进行评价：

式中：Umax和Ui分别为矿山所有巷道中地应力与巷道跨度的集合{Ui}中的最大值以及一般值。

围岩质量与支护方式越好，则巷道围岩顶板产生的位移就越小，也就越不容易破坏，因此，对Umax和Ui这2项指标采用下限效果测度进行评价：

式中：Umin和Ui分别为矿山所有巷道中围岩质量与支护方式评价值的集合{Ui}中最小值。根据各因素灰色效果测度的结果，建立所有巷道的统计决策矩阵R。

利用决策矩阵，并考虑各因素对软岩巷道顶板位移的影响，对多因素的总体灰色效果进行测量。由于各因素对巷道顶板位移的影响并不是等同的，因此，在决策中不能以算术平均值求得总体灰色效果测度，而应取加权平均值。

1.4 巷道顶板稳定性分析

对于巷道，其高度是严格按照相关标准设计的，当其顶板的位移超过一定值时，就意味着巷道部分或全部失去了使用价值，即当巷道顶板的位移超过数值ζ时，巷道即被视作被破坏[9]。

将样本巷道的顶板最终位移预测值与ζ进行比较，当最终预测值大于ζ时，巷道顶板即视为被破坏，其二次支护方式应取比较稳固的支护方式；当最终预测值小于ζ时，巷道视作安全有保证，其二次支护方式采取一般的支护方式即可。将样本巷道的顶板最终破坏情况与其总的灰色效果测度值对应，通过分析，找出总的灰色效果测度值ε1。当总的灰色效果测度不小于该值，即时，则巷道极有可能因顶板位移量过大而破坏，该软岩巷道顶板稳定性极差，巷道极有可能因顶板位移过大而被破坏。

找出另外一个灰色效果测度值ε2，当总的灰色效果测度值大于等于ε2而小于ε1，即

时，则巷道可能因顶板位移过大而破坏。该软岩巷道顶板稳定性较差，巷道可能因顶板位移而被破坏。

将由样本巷道得到的ε1以及ε2推广到矿山所有巷道，当巷道的综合灰色效果测度值大于ε1时，则该巷道顶板稳定性极差，其二次支护方式应慎重考虑，采取十分可靠的支护方法；当巷道的综合灰色效果测度值在ε2～ε1之间时，则巷道顶板稳定性较差，其二次支护方式应当仔细考虑，采取较可靠的支护方式；当巷道的综合灰色效果测度值小于ε2时，则巷道顶板稳定性较好，采取一般的支护方式进行二次支护即可满足要求[10−15]。

2 实例验证

2.1 巷道基本条件

某新建矿山巷道位于中粒砂岩、砂质泥岩、泥岩地层中，围岩属于软岩。由于顶板位移过大，矿山决定在巷道开挖支护3月后，对巷道进行二次支护。经统计，矿区巷道共有103条，其中：巷道跨度(净跨度，不包括支护厚度)大于等于4.5 m的巷道有13条；跨度大于等于3.0 m而小于4.5 m的巷道有67条；跨度小于3.0 m的巷道有23条。矿区巷道顶板所受的地应力(包括构造应力与自重应力)的范围为 22.37～76.19 MPa，围岩质量按 RMR标准测定，其评分值范围为23～57，巷道跨度范围为2.2～5.7 m，支护方式评分值范围为57.6～88.4。对矿区巷道统一编号后按巷道跨度分层抽样，选取具有代表性的 17条巷道作为样本巷道，其中：跨度大于等于4.5 m的巷道2条；跨度大于等于3.0 m而小于4.5 m的巷道有11条；跨度小于3.0 m的巷道有4条。样本巷道参数如表2所示。

2.2 顶板位移预测

在样本巷道的顶板上安装多点位移计进行位移监测，在3月内等时距地进行6次检测，其位移监测结果见表3。

由于软岩巷道自身的不稳固性，在样本巷道的观测过程中，58号巷道已经破坏，这也说明进行巷道位移预测及破坏情况判定对指导二次支护工作的重要性。

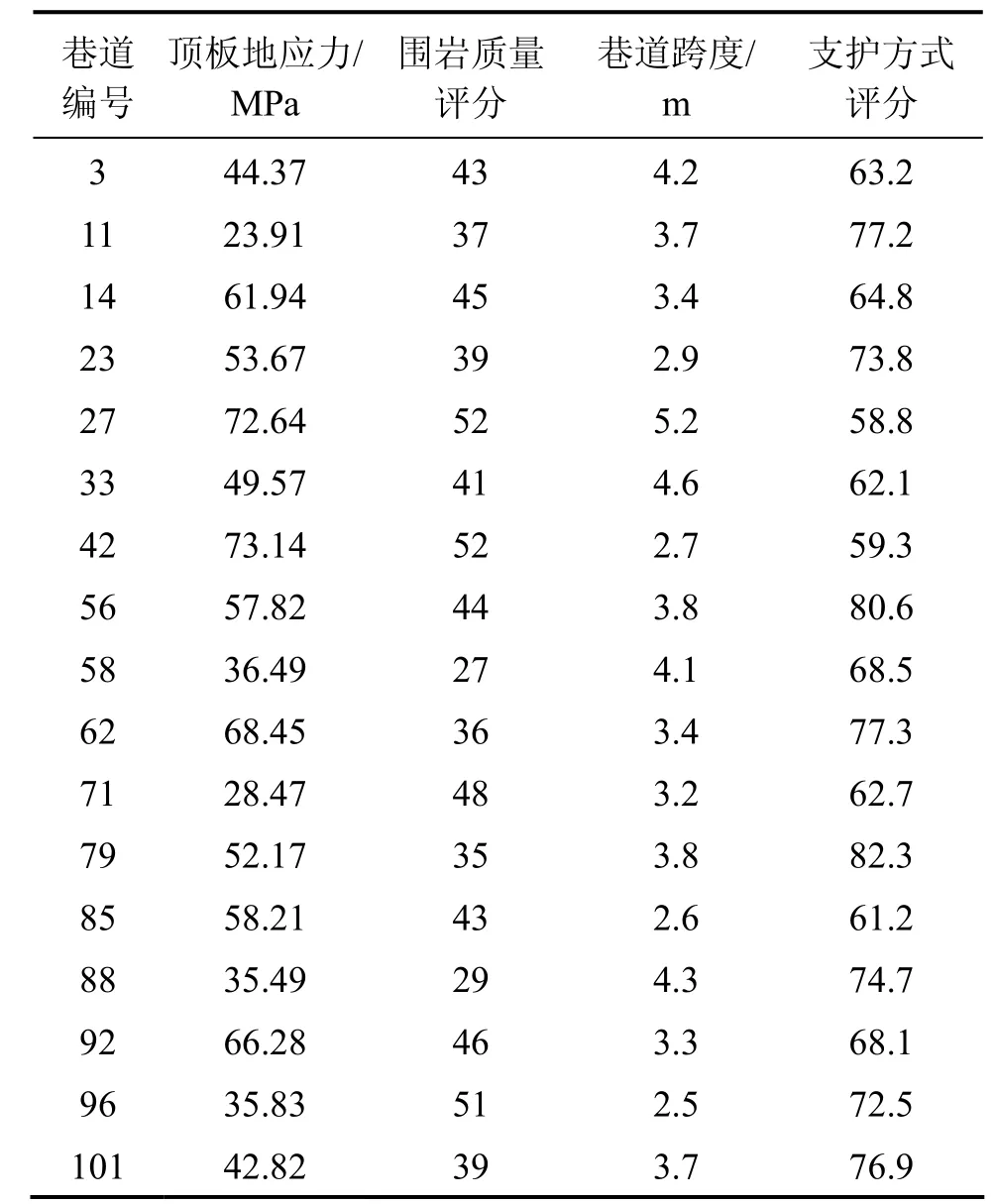
表2 样本巷道基本参数Table2 Basic parameters of sample roadways

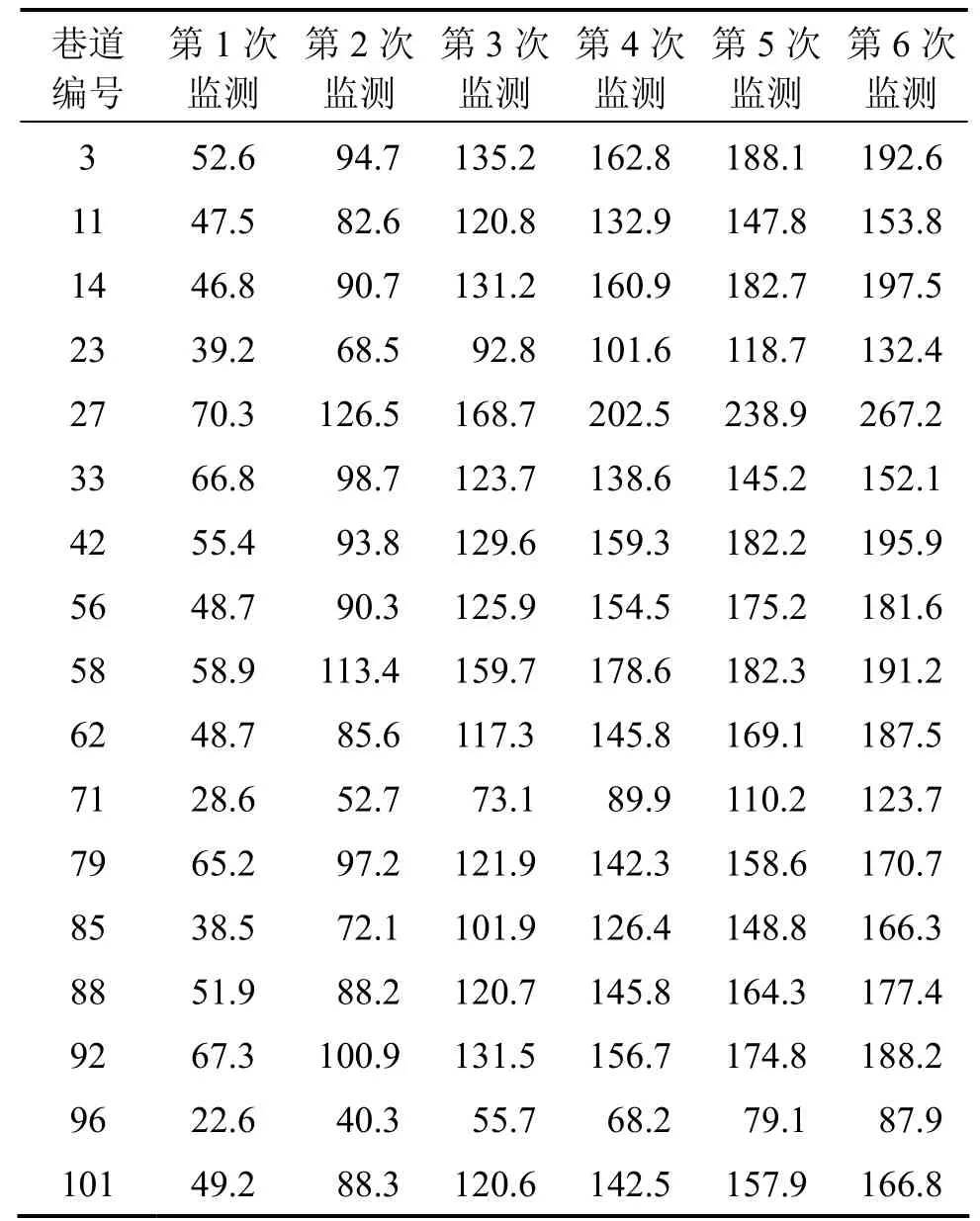
表3 顶板位移监测结果Table3 Monitoring results of displacement of final roof mm

以3号巷道为例，利用改进Verhulst模型对最终位移进行预测。

3号巷道的位移观测值原始数据为X(1)=(52.6,94.7, 135.2, 162.8, 188.1, 192.6)，则X(1)的 1-IAGO 序列X(0)以及紧邻均值生成序列Z(1)分别为：

根据3号巷道的位移观测值原始数据序列、1-IAGO序列以及紧邻均值生成序列，按式(5)构造矩阵：

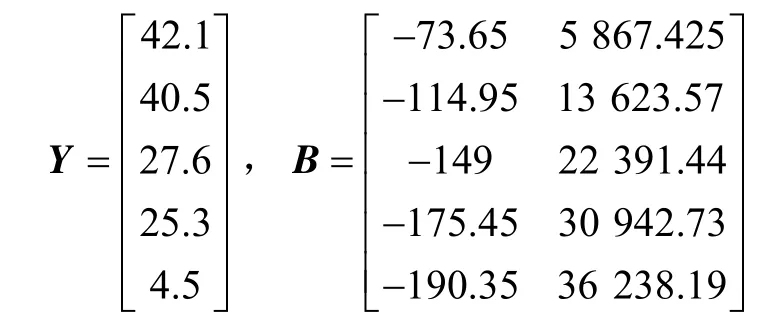
利用上述矩阵按式(6)对灰参数序列a=[a,b]T进行最小二乘估计，得到灰参数序列为：

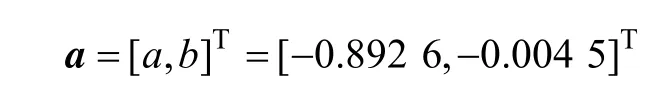
取x(1)(1)= 5 2.6，按式(9)得到差分Verhulst的时间响应式为：

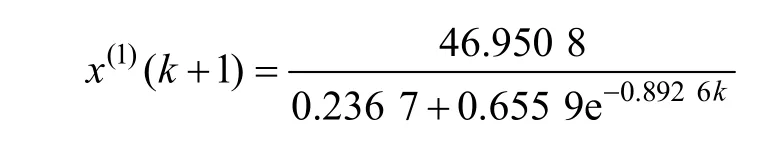
对改进后的Verhulst模型进行误差检验，并与传统的Verhulst模型的精度进行比较，其结果如表4所示。

根据上述结果，参照《灰色预测模型精度检验等级表》，改进Verhulst模型与传统Verhulst模型的精度等级均为一级，可以进行长期数据预测。但改进Verhulst模型的相对精度比传统 Verhulst模型的相对精度要高，其残差平方和比传统的Verhulst模型的残差平方和要小，因此，改进Verhulst模型精度高于传统Verhulst模型精度，预测软岩巷道最终顶板位移更加准确，这对于软岩巷道顶板位移出现小量偏差便可能酿成重大事故的情况，该方法更加有用，采用该方法预测出3#巷道顶板的最终位移为199.3 mm。对所有样本巷道利用改进后的Verhulst模型对最终位移进行预测，对于该矿山，当其巷道顶板最终位移大于 200 mm时，便可视作巷道被破坏，其结果如表5所示。

2.3 灰色效果测度

对样本巷道灰色效果进行测度。对巷道中的顶板地应力与巷道跨度，其测度值越大，巷道顶板位移也就越大。因此，对这2项指标采用上限效果测度进行评价，对于顶板地应力，其上限值为 76.19 MPa；对于巷道跨度，其上限值为5.7 m。对于巷道中的围岩质量评分与巷道支护评分，其值越大，巷道顶板位移也就越小，因此，对这2项指标采用下限效果测度进行评价。对于围岩质量评分，其下限值为23；对于巷道支护评分，其下限值为 57.6。利用式(10)对顶板地应力与巷道跨度的灰色上限效果进行测度，利用式(11)对围岩质量评分与巷道支护评分的灰色下限效果进行测度，最终得到样本巷道各影响因素的灰色效果测度值如表6所示。

根据相对重要程度相关等级计算法确定巷道顶板位移影响因素的权重矩阵为W=[顶板地应力，围岩质量评分，巷道跨度，支护方式评分]=[0.36, 0.22, 0.25,0.17]，利用巷道顶板位移影响因素的灰色效果测度值构建决策矩阵R，按式(12)对决策绝阵与权重矩阵根据加权平均算法的关系进行合成，得到综合灰色效果测度矩阵A。将样本巷道的综合灰色效果测度值与巷道破坏情况对应，其结果如表7所示。

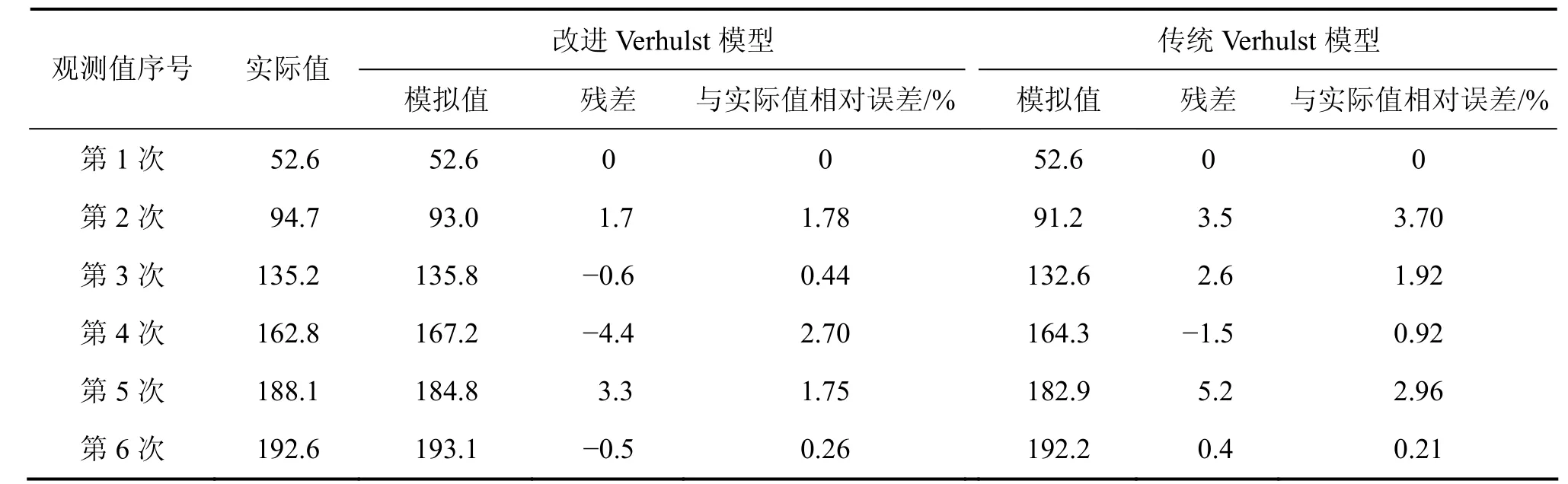
表4 改进Verhulst模型与传统的Verhulst模型精度比较Table4 Improved Verhulst model with traditional Verhulst model accuracy comparison

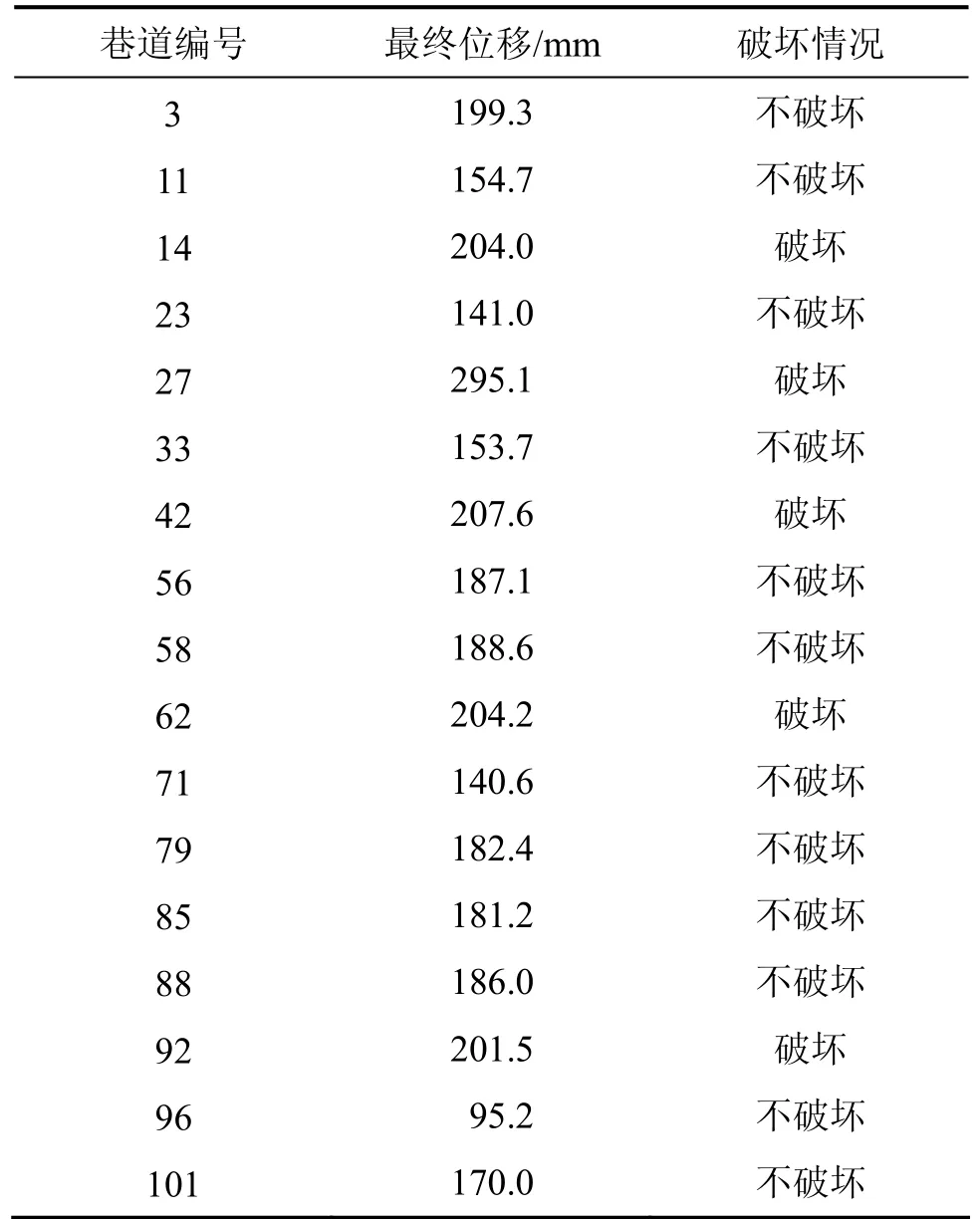
表5 样本巷道顶板最终位移Table5 Final roof displacement of sample roadways mm

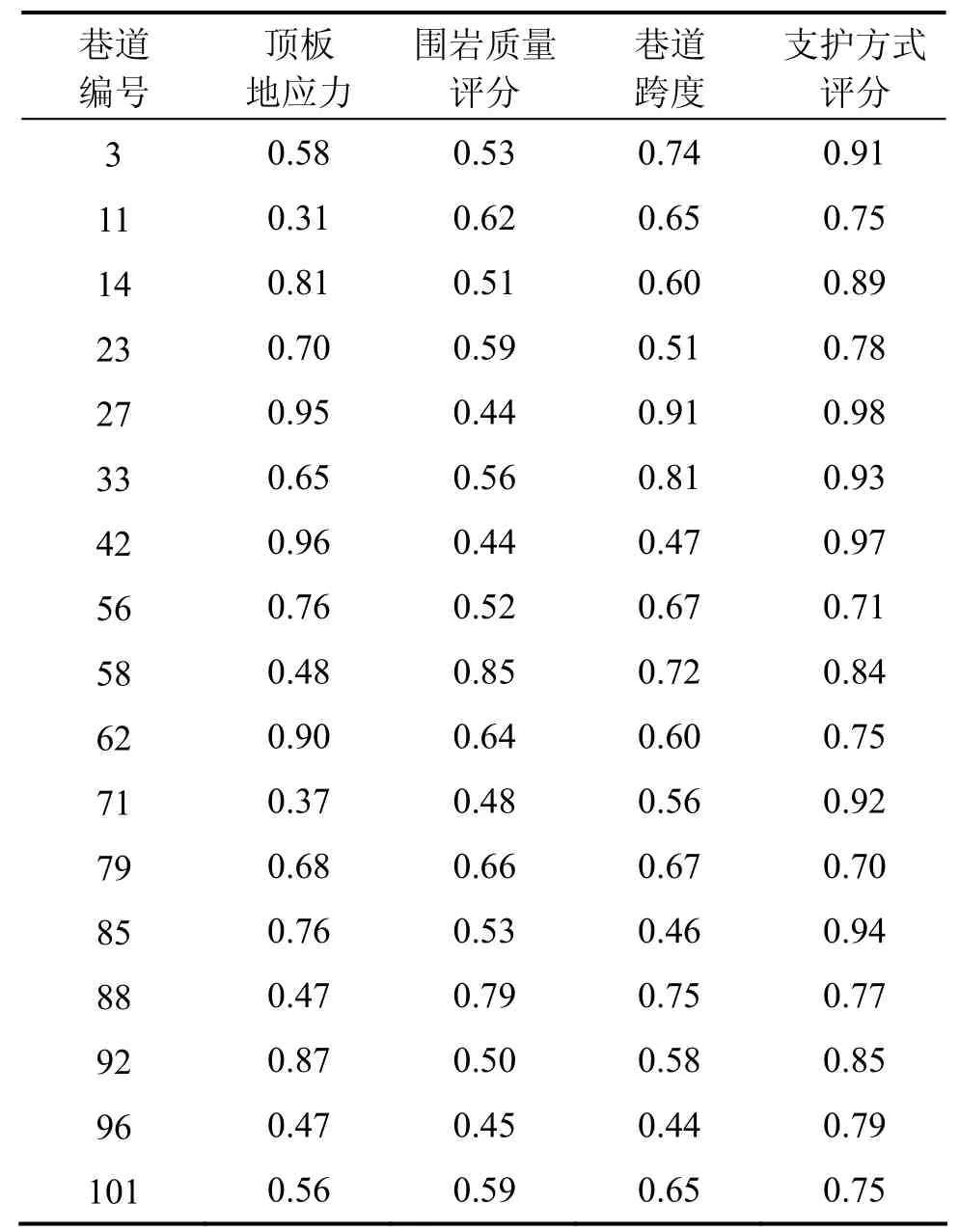
表6 样本巷道顶板位移影响因素灰色效果测度值Table6 Grey measurement Tableof roof displacement affecting factors of sample roadways

表7 样本巷道顶板破坏规律分析Table7 Roof failure pattern analysis of sample roadways

2.4 结果分析

由表7可以看出：破坏巷道的最小综合灰色效果测度值为0.705 1，即只要巷道综合灰色效果测度值大于等于0.705 1时，巷道即有可能因顶板位移过大而破坏。在不破坏巷道中，其最大综合灰色效果测度值为0.717 8，破坏巷道综合灰色效果测度值大于此值的最小值为0.724 8，因此，可以得到如下规律：

(1)当巷道总的灰色效果测度值为[0.724 8, 1]时，巷道极有可能因顶板位移过大而破坏，则该软岩巷道顶板稳定性极差。

(2)当巷道总的灰色效果测度值为[0.705 1, 0.724 8)时，则巷道极有可能因顶板位移过大而破坏，该软岩巷道顶板稳定性较差。

(3)当巷道总的灰色效果测度值为[0, 0.705 1)时，则巷道最终顶板位移还是处于比较安全的范围之内，不会因位移过大而破坏，该软岩巷道顶板稳定性较好。

对矿山所有的103条巷道的综合灰色效果测度值进行计算。将上述规律推广到矿山所有巷道。按巷道顶板稳定性不同将矿区巷道分级成为顶板极不稳定巷道、顶板较不稳定巷道与顶板较稳定巷道，对顶板极不稳定巷道，采用喷射混凝土加钢筋网加锚杆的二次支护方式；对顶板较不稳定巷道，采用喷射混凝土加锚杆的二次支护方式；对顶板较稳定巷道，采用喷射混凝土的二次支护方式。

在采用二次支护方式2 a内，只有4条巷道出现了因顶板位移过大而产生的局部破坏，破坏巷道数仅占矿山巷道数的 3.89%，大大低于相似矿山的巷道破坏比例。

3 结论

(1)采用 Verhulst模型可以预测数据曲线具有“S”形特征的情况；与传统的Verhulst模型相比，改进Verhulst模型具有更高的预测精度。

(2)灰色效果测度算法可以忽略各影响因素的影响，对巷道顶板位移影响因素能进行综合、客观可靠的评价。将样本巷道顶板位移影响因素综合灰色效果测度值与样本巷道最终破坏情况进行对应，得出巷道顶板稳定性分级标准，根据分级标准对巷道顶板稳定性进行分析，根据顶板稳定性分析结果指导软岩巷道的二次支护工作。

(3)在选取巷道围岩顶板位移的影响因素时，应尽量全面考虑。选取的因素越全面，所得出的规律可靠性就越高。

[1]王光颖.巷道围岩应力场分布分析方法探讨[J].煤炭科学技术, 2003, 31(7): 44−46.WANG Guang-ying.Discussion on analysis method for stress field distribution in surrounding rocks of mine roadway[J].Science and Technology of Coal, 2003, 31(7): 44−46.

[2]贾蓬, 唐春安, 王述红.巷道层状岩层顶板破坏机理[J].煤炭学报, 2006, 31(1): 11−15.JIA Peng, TANG Chun-an, WANG Shu-hong.The roof damage mechanism of layered rock roadway[J].Journal of Coal, 2006,31(1): 11−15.

[3]姜耀东, 赵毅鑫, 刘文岗, 等.深部开采中巷道底鼓问题的研究[J].岩石力学与工程学报, 2004, 23(14): 2396−2401.JIANG Yao-dong, ZHAO Yi-xin, LIU Wen-gang, et al.Research on floor heave of roadway in deep mining[J].Chinese Journal of Rock Mechanics and Engineering, 2004, 23(14):2396−2401.

[4]李文远.析巷道破坏与其位置和支护方式的关系[J].淮南职业技术学院学报, 2006, 5(3): 10−12.LI Wen-yuan.Analysis roadway destruction with location and the supporting method[J].Journal of Huainan Vocational and Technical College, 2006, 5(3): 10−12.

[5]王正新.GM(1,1)模型的特性与优化研究[D].南京: 南京航空航天大学经济与管理学院, 2007: 39−43.WANG Zheng-xin.Study on the characteristics and optimization of GM(1,1)model[D].Nanjing: Nanjing University of Aeronautics and Astronautics.College of Economics and Management, 2007: 39−43.

[6]宋彦辉, 聂德新.基础沉降预测的灰色Verhulst模型[J].岩土力学, 2003, 24(1): 13−16.SONG Yan-hui, NIE De-xin.Grey base settlement Verhulst model[J].Rock and Soil Mechanics, 2003, 24(1): 13−16.

[7]刘玉成.改进的灰色Verhulst GM(1,1)建筑物沉降模型[J].中国地质灾害与防治学报, 2006, 17(4): 61−63.LIU Yu-cheng.Improved gray like Verhulst GM(1,1)building subsidence model[J].The Chinese Journal of Geological Hazard and Control, 2006, 17(4): 61−63.

[8]罗云, 吕海燕, 白福利.事故分析预测与事故管理[M].北京:化学工业出版社, 2005: 12.LUO Yun, LÜ Hai-yan, BAI Fu-li.Accidents and accident analysis and prediction[M].Beijing: Chemical Industry Press,2005: 12.

[9]陈秀友.任楼煤矿巷道破坏原因分析与治理对策[D].徐州:中国矿业大学矿业工程工程学院, 2008: 24−25.CHEN Xiu-you.Reasons analysis and control methods on roadway damage of Renlou Coal Mine[D].Xuzhou: China University of Mining and Technology.Mining Engineering College, 2008: 24−25.

[10]邱淑芳, 周其华, 王泽文.改进的GM(1, 1)模型及其在地下水环境预测中的应用[J].东华理工学院学报, 2006, 29(2):176−180.QIU Shu-fang, ZHOU Qi-hua, WANG Ze-wen.Improvement of GM(1,1)model and its application on groundwater environments prediction[J].Journal of East China Institute of Technology,2006, 29(2): 176−180.

[11]李秀珍, 孔纪名, 王成华.灰色 GM(1,1)残差修正模型在滑坡预测中的对比应用[J].山地学报, 2007, 25(6): 741−746.LI Xiu-zhen, KONG Ji-ming, WANG Cheng-hua.Comparison and application of grey GM(1,1)modified residual error models in landslide predicting[J].Journal of Mountain Science, 2007,25(6): 741−746.

[12]肖有才, 张秀成, 王宏艳.灰色理论在预测深埋型矿井涌水量中的应用[J].辽宁工程技术大学学报, 2004, 23(2): 175−177.XIAO You-cai, ZHANG Xiu-cheng, WANG Hong-yan.Application of grey theory model in prediction of pit water discharge in coal mine[J].Journal of Liaoning Technical University, 2004, 23(2): 175−177.

[13]Yeh M F, Lu H C.A new modified grey model[J].The Journal of Grey System, 1996, 8(3): 209−216.

[14]DENG Ju-long.Solution of grey differential equation for GM(1,1|τ,r)in matrix train[J].The Journal of Grey System, 2002,14(1): 105−110.

[15]Wu J H, Lau C R.A study to improve GM(1,1)via heuristic method[J].The Journal of Grey System, 1998, 10(3): 183−192.