一种新的用于编制露天矿生产计划开采模型

黄俊歆 ，郭小先，王李管，谭正华，毕林，李德，陈建宏

(1.中南大学 资源与安全工程学院，湖南 长沙，410083；2.湖南工学院 安全与环境工程系，湖南 衡阳，421001；3.西部矿业股份有限公司，青海 西宁，810001；4.玉溪矿业有限公司，云南 玉溪，653100)

编制露天矿采掘进度计划的总目标是确定一个技术上可行且能够使总体经济效益最大化的矿岩采剥顺序。矿床开采的总体经济效益最大是指从动态经济观点出发，使矿床开采中实现的总净现值最大；技术上可行是指采掘进度计划必须满足一系列技术上的约束条件，主要包括：(1)在每一个计划期内为选厂提供较为稳定的矿石量和入选品位；(2)每一计划期的矿岩开采量应与可利用的采剥设备的生产能力相适应；(3)各台阶水平的推进必须满足正常生产要求的时空发展关系，即最小工作平盘宽度、安全平台宽度、工作台阶的超前关系、采场延深与台阶水平推进的速度关系等[1]。目前，国内编制露天矿采掘进度计划普遍采用手工方法，即使借助计算机，现在已有的辅助设计软件都只是提供模拟手工操作的方法，无法准确考虑上述技术约束条件，导致编制出来的露天矿采掘计划难以指导生产。国外发达国家通常利用计算机来解决露天矿生产计划编制问题(Open-pit mine production scheduling problems, OMPSP)。最初有研究者提出利用LG图论法[2]或浮锥法[3]通过调整价值模型分别进行计算，得出一系列嵌套分期境界作为各计划期的期末图，但这种方法无法满足采掘进度计划的技术约束条件，而且试算法调整价值模型的工作量非常大。随后又相继产生 heuristics算法[4]、Korobov算法[5]、参数化算法[6]、动态规划法[7]、混合整数规划法[8]，等等。其中：混合整数规划法能够充分考虑露天矿生产计划编制问题的一系列技术约束条件，该算法的时间复杂度为指数阶[9]，因计算量太大，该方法仅在理论上可行，无法解决实际的大规模 OMPSP。Natashia等[10]针对OMPSP从优化线性规划问题求解算法的角度进行研究，有效地降低了其时间复杂度，但该方法实现难度非常大。在此，本文作者提出一种基于成本流的开采锥模型(CFCM)。采用图论的方法将正价值块与其开采锥内相关负价值块聚合，减少了混合整数规划模型中的变量个数，降低了计算复杂度，从而使解决实际的大规模OMPSP变成可能。此外，通过工程实例验证了该模型的有效性及可行性。

1 露天矿生产计划编制流程

将矿床划分为有限个尺寸相等的长方体(包括开采的矿石和剥离的废石)，每个块体形成的离散模型称为矿床块段模型。采用矿体解译、地质资料分析等方法，通过估值使块段模型中每一块的净价值变为已知，估值后的块段模型称为价值块段模型。露天矿境界优化流程图见图1。

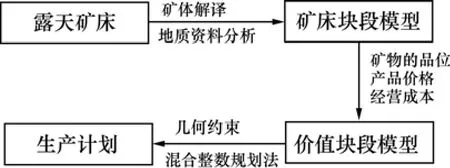
图1 露天生产计划编制流程图Fig.1 Flow chart of open-pit mine production scheduling

块段净价值是根据块中所含可利用矿物的品位、经营成本及产品价格计算的。由于矿床所含矿物的多样性及矿山企业经营体制和成本管理制度的差异，计算净价值时用到的参数并不固定。其净价值计算方法见图2。其中：每个块体的值表示开采该块体的净利润，剥离的废石为负值，Vore=Vo−Com−Cot−Cor−Cp−Cs；Vwaste=−Cwm−Cwt−Cwr。

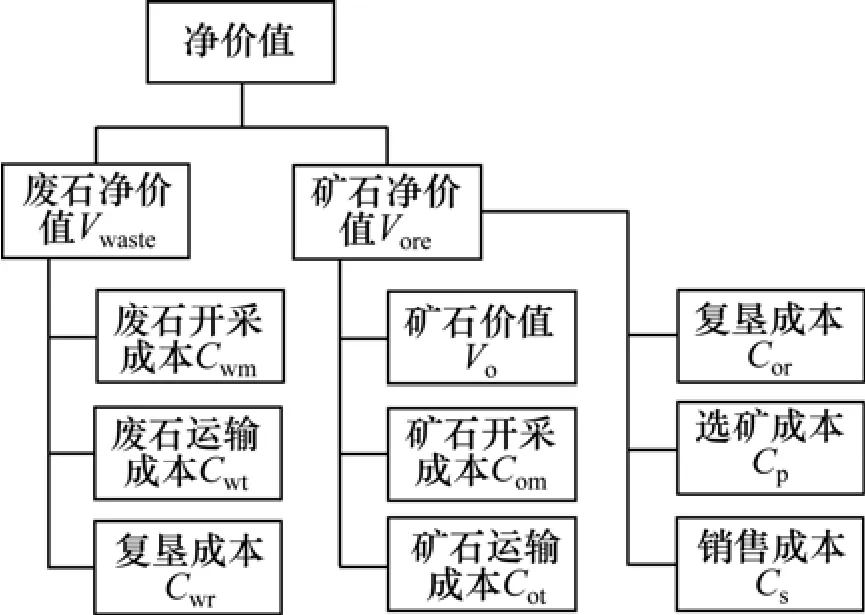
2 CFCM模型的构建

实际的露天矿矿床块段模型的块数通常在 106数量级以上。构建混合整数规划计算模型时，为了充分考虑露天矿生产计划约束条件，必须为每一个块建立一个整数变量(0表示不开采，1表示开采)。这样一个大型的混合整数规划问题，对现有的计算机软、硬件技术来说是无法实现的。

2.1 基本原理

为便于叙述CFCM模型的基本原理，采用图3所示的简单二维块段模型进行阐述，以块段的中心点表示该块段(以下称节点)。

在满足工作帮坡角几何约束条件的前提下，只考虑开采矿床块段模型中某一正价值节点，该节点记为Ni，其净价值记为Vi，其上方所有必须先开采的负价值节点的净价值代数和即为开采正价值节点Ni所须承担的成本。节点Ni与其上方所有必须先开采的节点形成1个倒圆锥，称为正价值节点Ni的开采锥，记为Ci；开采锥Ci的顶点为Ni，正价值节点Ni与其开采锥内某负价值节点Nj之间以有向边相连，该有向边表示节点Ni与节点Nj之间的成本流，记为fij；该开采锥顶点Ni与锥内所有负价值节点的价值代数和称为开采锥的锥价值，记为Vci。矿床块段模型中的所有正价值节点都与其开采锥内的负价值节点以有向边相连，在其底部加一源节点，记为S；在其顶部加一汇点，记为T。形成的有向图称为初始CFCM，如图3所示。

这样，矿床块段模型中每一正价值节点都与其上所有可能对其构成成本负担的负价值块以成本流连接，但节点作为模型中的最小单元，每一个负价值节点只可能对1个正价值节点构成成本负担。以此作为理论基础，采用线性规划方法对初始CFCM进行成本最优分配。构建混合整数规划计算模型时，其整数变量个数也从原来的矿床块段模型节点总数减少为其正价值节点数，极大地减少了整数变量个数，降低了计算复杂度。

2.1.1 构建线性规划模型目标函数

对于一个给定的矿床块段模型，在其最终开采境界内的所有负价值节点的价值代数总和为定值，即总开采成本为定值，则其成本流之和也为一定值，即∑fij为定值。

为力求早投产、快达产、缩短基建期、减少基建投资，应从最先能开采到正价值块处开始开采，从而达到尽快回收成本的目的。这样，就应该使成本流尽量地流向价值更大的开采锥。依据该原则构建如图3所示的线性规划模型。

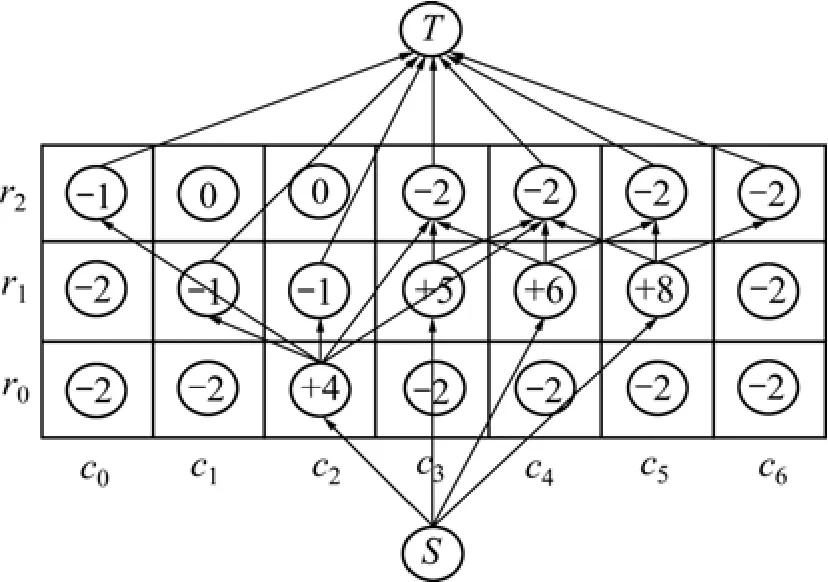
图3 二维块段模型及初始CFCM模型Fig.3 2D block model and initial CFCM model

图3所示为简单二维块段模型的CFCM模型初始图，为便于阐述，令工作帮坡角为 45°。构建模型的具体步骤如下。

(2)为每个正价值节点按其CV分配 1个权值系数，记为Ce。将所有节点按其在块段模型中的层号从大到小排序(坐标系统如图4所示)，层号相同的按其CV从大到小排序，权值系数Ce则按排好序的节点。其Ce则按该顺序从小到大分配，下一层的各正价值块的Ce则从上一层最大Ce开始分配。

(3)构建目标函数。该线性规划模型的目标是使成本流尽量地流向价值更大的开采锥，因此，取上述分配了权值系数的表达式的最小值作为线性规划模型的目标函数，即

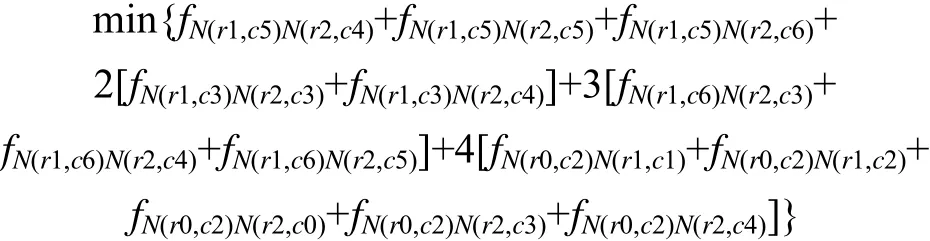
注：fN(r1,c5)N(r2,c5)表示节点N(r1,c5)流向节点N(r2,c5)的成本流，其他项类同。

2.1.2 构建线性规划模型约束条件

由于成本流是从源点流出，流向汇点，根据图的性质，有：

(1)中间任意节点流入的与流出的成本流代数和为0；对于正价值节点Ni，有：价值节点Nj，有：

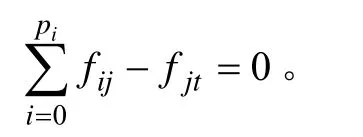
(2)从源点流向正价值节点的成本流不大于该节点的价值，即：fSi≤Vi；

(3)从负价值节点流入汇点的成本流等于该节点的价值，即：fjT=Vj。

其中：S表示源点；T表示汇点；i表示正价值节点；j表示负价值节点；ni表示从正价值节点Ni引出的有向边条数；pi表示指向负价值节点Nj的有向边条数。

因此，对于图3所示的简单块段模型，其线性规划模型约束条件如下：

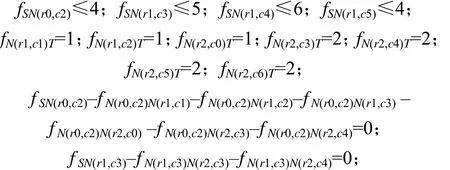
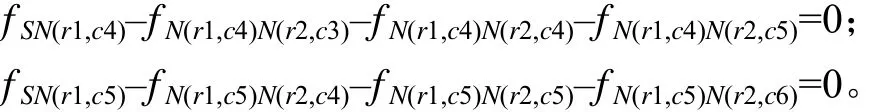
2.2 算法描述

建立图4所示的坐标系统，XYZ坐标系为世界坐标系，其值为块段的真实坐标值；ijk坐标系为相对坐标系，其值为块段在矿床块段模型中的序号。

2.2.1 CFCM构建算法

第1步：形成初始图。遍历所有节点，当前节点记为Ni，若节点Ni为正价值节点，将节点Ni与其开采锥内所有负价值节点以有向边相连，正价值节点Ni与负价值节点Nj间的有向边记为fij。同时，将Ni存入正价值节点数组中。

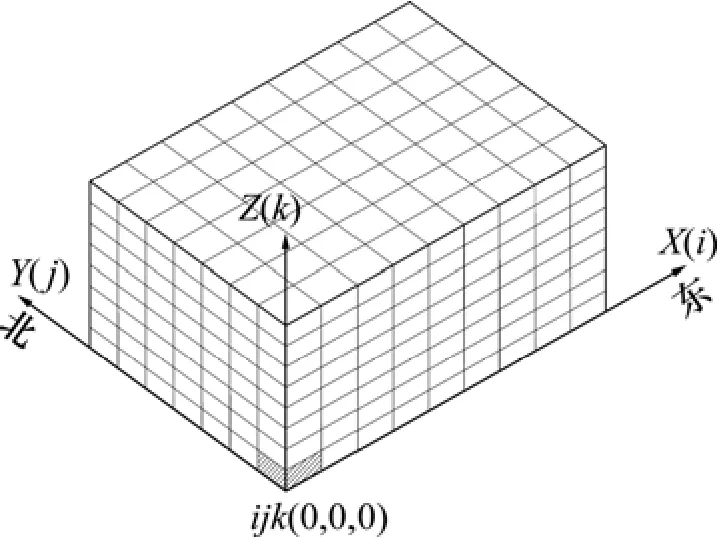
图4 三维块段模型坐标系统Fig.4 Coordinate system of 3D block model

第2步：计算锥价值。遍历所有正价值节点，当前节点记为Ni，节点Ni及所有与它以有向边相连的负价值节点的价值代数和即为节点Ni的锥价值。

第3步：赋权系数。将正价值节点数组中所有节点按其在块段模型中的层号从大到小排序，层号相同时按节点的锥价值从大到小排序。在排序后的数组中，第1个节点权系数Ce1为1，第2个节点权系数Ce2为2，依此类推，第n个节点权系数Cen为n。

第4步：建立线性规划模型。

第5步：求解线性规划问题，遍历结果中所有成本流，当前成本流记为fij。若fij为0，则将节点Ni与节点Nj之间的有向边删除。删除所有为0的成本流后形成新的CFCM，执行第2步；若无结果为0的成本流，则程序结束，得到最终CFCM。

2.2.2 线性规划模型算法的建立

第1步：构建目标函数。遍历所有正价值节点，共有m个正价值节点，当前节点记为Ni；其权系数为Cei；Ni引出的成本流有n条，记为f1～fn。则目标函数

第2步：构建约束条件。

(1)遍历所有从源点S流出的成本流，共有x条，当前成本流记为fSi，流向正价值节点Ni，Ni的价值为Vi。据此可以构建出x个约束条件：fSi≤Vi；1≤i≤x

(2)遍历所有流入汇点T的成本流，共有y条，当前成本流记为fjT，从负价值点Nj流出，Nj的价值为Vj。据此可以构建出y个约束条件：fSi=|Vj|；1≤j≤y

(3)遍历所有正价值节点，共有z个正价值节点，当前节点记为Ni，流入该节点的成本流有u条，记为fiI1～fiIu；从该节点流出的成本流有v条，记为fiO1～fiOv；据此可以构建出z个约束条件：1≤i≤z。

3 实例应用

3.1 三维地质模型的创建

基于CFCM的算法已用于DIMINE数字矿山系统中。以云南某矿为研究对象，用DIMINE创建了该矿的空间地质数据库、数字地形模型(Digital Terrain Model，DTM)[9−11]、矿体模型、矿床品位块段模型，见图5，这些资料是该矿露天矿生产计划编制工作的基础。

图5 DTM、钻孔空间位置及主要矿体分布Fig.5 DTM and drill spatial location and main orebodies distribution

矿体呈北西向北东呈波状缓倾斜，倾角为 10°～25°，局部大于 35°。地面标高 1.21 km，矿体总体长2.00 km，宽100～670 m，埋深从地表到280 m标高，矿体厚度为2～50 m，平均品位约0.4%。矿体形态较复杂，呈多个不规则的透镜体或构造块体。同一矿体厚度与品位变化较大。

本次建立地质数据库包含钻孔486个，测斜数据2 246条，所有钻孔、槽探和坑探取样38 411个。矿床主要有Ⅰ号、Ⅱ号、Ⅲ号3个矿体，其中Ⅱ和Ⅲ号矿体储量大，为该矿区的主要矿体，块段模型创建中选择单元块长×宽×高为10 m×20 m×4 m。矿体分布情况及最终设计境界见图6。

图6 矿体分布情况及最终设计境界(即范围)Fig.6 Ore bodies distribution and its final designed limit

3.2 露天矿生产计划编制参数选择

3.2.1 经济参数的选取

此次优化的参数主要来源于地质报告、选矿实验指标和根据目前开采技术条件下通过工程类比法选取出相关指标，本例以云南某露天矿的3 a采剥计划编制为例。其主要优化参数见表1。

3.2.2 优化参数的选取

在计划编制过程中，按照矿山的选厂处理能力等实际情况，确定6 000 t/d方案各年采矿量为：第1年75万t，第2年150万t，第3年以后按照198万t进行编排，直至减产结束。矿量容差为 5%，各年品位及剥采比约束如表2所示。

3.3 结果分析

将上述参数输入DIMINE软件露天矿生产计划编制模块中。矿床块段模型XYZ3个方向的块数为89×55×93，共455 235块；但其中正价值块数仅为75 315块。利用CFCM构建计算模型，采用混合整数规划法进行露天矿生产计划编制，其整数变量数从455 235个减少到75 315个，极大地减少了计算量。

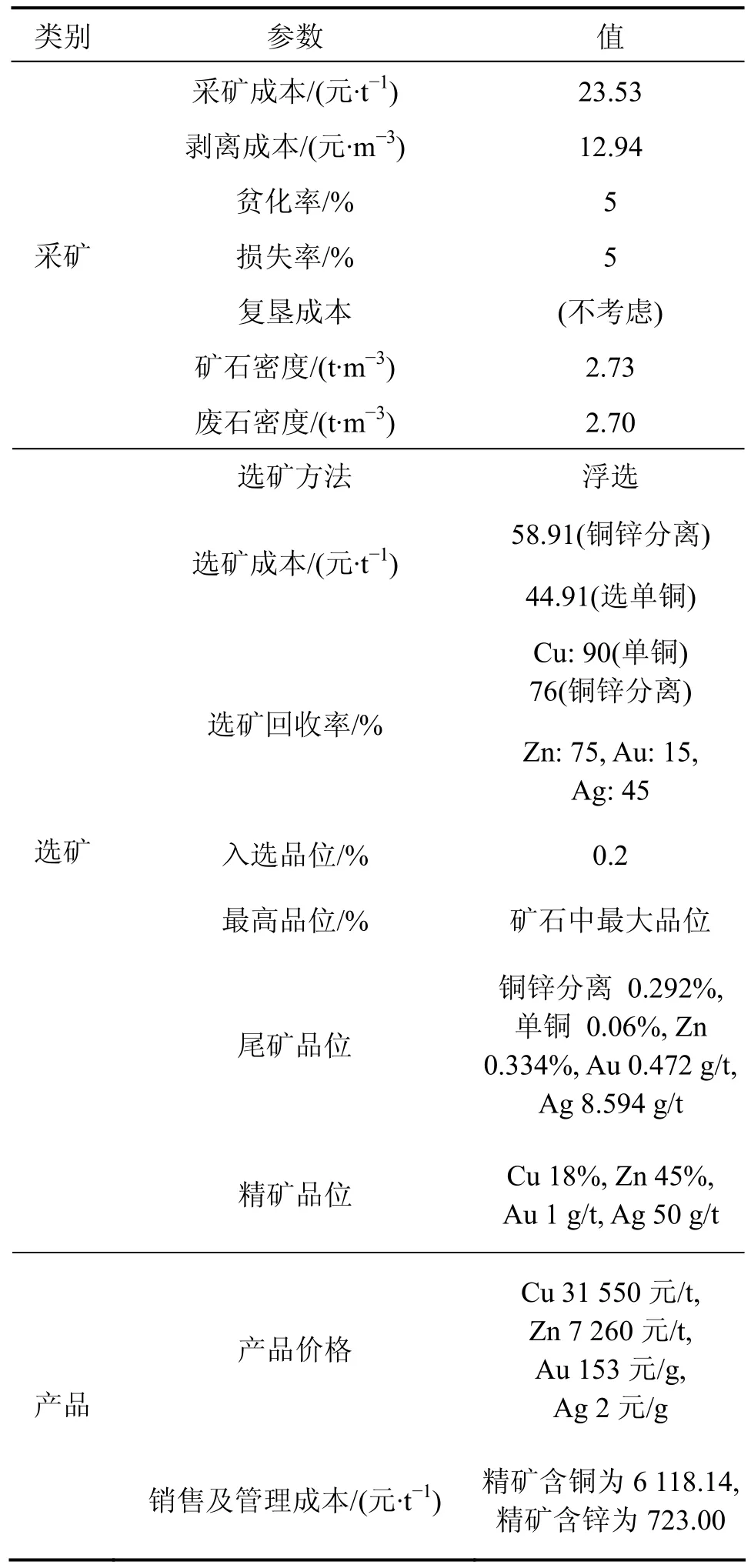
表1 优化参数表Table1 Optimal parameters table

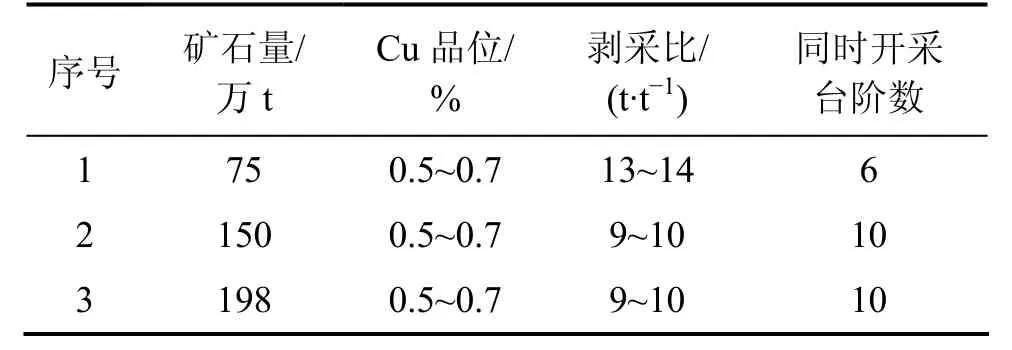
表2 优化参数表Table2 Optimal parameters table

经计算，得到各年度采剥块段集合。在该结果数据为指导的基础上进行生产计划设计，其设计结果见图7，采剥量见表3。

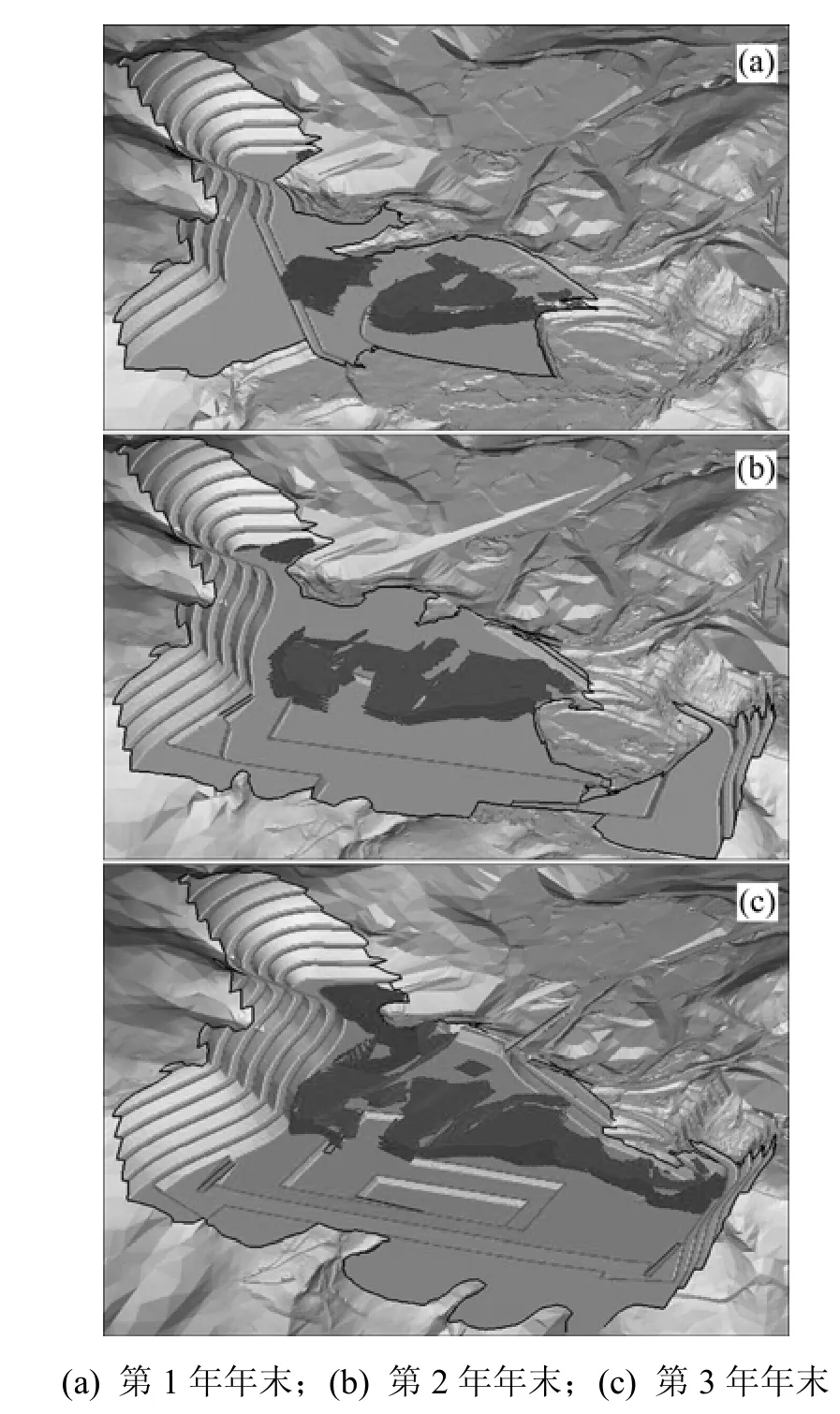
图7 露天矿生产计划设计结果Fig.7 Design results of open pit mine production scheduling

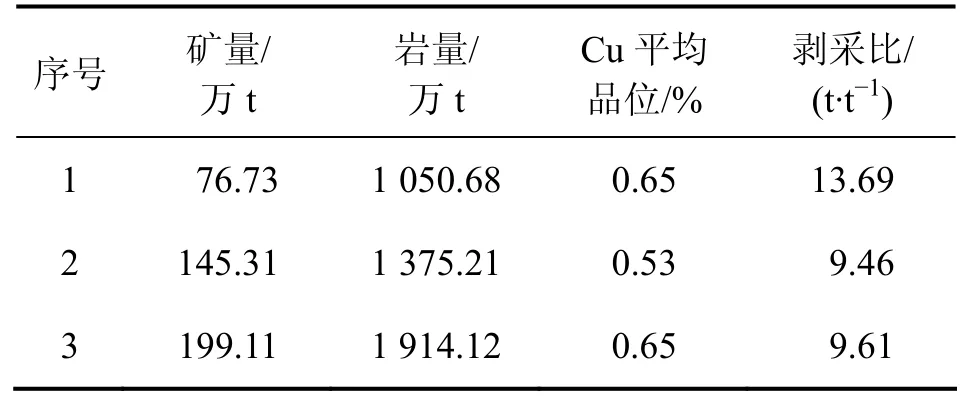
表3 各年度采剥量Table3 Stripping quantity for each year

4 结论

(1)针对采用混合整数规划法求解 OMPSP时的高复杂度，提出了一种新的露天矿开采锥模型即CFCM。CFCM 能够极大地减少采用混合整数规划法求解OMPSP时的整数变量个数，为解决OMPSP提供了一种新的有效方法。

(2)CFCM 的不足之处在于其依赖于规则三维块段模型，块段的细分程度及各个方向的尺寸对工作帮坡角的精度影响很大。然而，混合整数规划算法为指数复杂度，块段划分过细将会导致计算量过大。如何构建一种不规则块段模型，通过调整不同台阶、不同工作地点的块段尺寸、形状、细分程度来更精确地模拟工作帮坡角、开采条带等，是未来露天矿开采锥模型构建技术的难点与发展方向。

[1]王青.采矿学[M].北京: 冶金工业出版社, 2007: 344−394.WANG Qin.Mining science[M].Beijing: Metallurgy Industry Press, 2007: 344−394.

[2]Lerchs H, Grossmann I F.Optimum design of open pit mines[J].CIM Bull, 1965, 58(633): 47−54.

[3]Lemieux M.Moving cone optimizing algorithm[C]//Computer methods for the 80s in the Mineral Industry.New York, 1979:329−345.

[4]Gershon M.Heuristic approaches for mine planning and production scheduling[J].International Journal of Mining and Geological Engineering, 1987, 5(1): 1−13.

[5]Yegulalp T M, Arias J A.A fast algorithm to solve the ultimate pit limit problem[C]//Proc of 23rd Symposium on the Application of Computers and Operations Research in the Mineral Industries (APCOM).Colorado, 1992: 391−397.

[6]Dowd P A, Onur A H.Open-pit optimization.part 1: Optimal open-pit design[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(1):95−104.

[7]Wilke F L, Wright E A.Determining the optimal ultimate pit design for hard rock open pit mines using dynamic programming[J].Erzmetall, 1984, 37(3): 139−144.

[8]Caccetta L, Hill S P.An application of branch and cut to open pit mine scheduling[J].Journal of Global Optimization, 2003,27(2/3): 349−365.

[9]Natashia B, Irina D, Gary F, et al.LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity[J].Computers &Operations Research, 2007, 36(4): 1064−1089.

[10]庞碧君.线性规划与随机规划[M].郑州: 郑州大学出版社,2009: 1−16.PANG Bi-jun. Linear programming and stochastic programming[M].Zhengzhou: Zhengzhou University Press,2009: 1−16.

[11]周智勇, 陈建宏, 杨立兵.大型矿山地矿工程三维可视化模型的构建[J].中南大学学报: 自然科学版, 2008, 39(3):423−428.ZHOU Zhi-yong, CHEN Jian-hong, YANG Li-bing.3D visualization modeling on geological and mining engineering in a large-sized mine[J].Journal of Central South University:Science and Technology, 2008, 39(3): 423−428.