VBA 在均质土坝渗流计算中的应用

宁鹏飞，许经宇，高乃东，陈中竹

（吉林省水利水电勘测设计研究院，吉林 长春 130021）

在水利工程中，土坝渗流量计算和浸润线的位置确定是土坝设计的重要工作，常常通过渗流量及浸润线确定土坝的安全性。在计算时，根据坝体上下游水位、坝体形状及材料等参数采用试算法确定浸润线方程。由于人工计算工程量大而且误差大，因此本文引用Excel中的VBA编程进行计算，大大地提高了计算的速度和精度。

1 计算理论及试算原理

在土坝设计中，各种土坝如均质土坝、粘土心墙土坝、斜墙土坝无排水设备和贴坡排水等渗流计算理论基本相同，文章将以不透水地基上均质土坝为例来论述VBA的渗流计算中应用（如图1所示）。

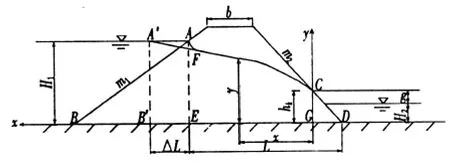
图1 筑于水平不透水地基上的均质土坝图

土坝渗流常假定为平面问题去进行分析，一般采用两段法，建立上游段流量方程和下游段流量方程，通过方程联立来求出浸润曲线下游溢出点的高度及单宽流量。

上游段所通过的单宽渗流量为：

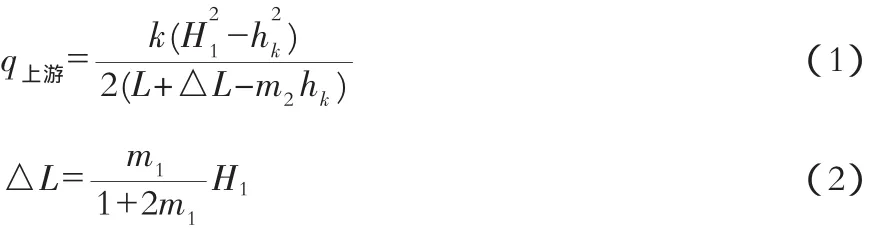
下游段所通过的单宽流量为：

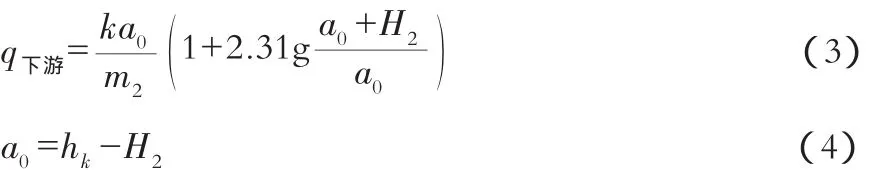
浸润曲线的方程式为：

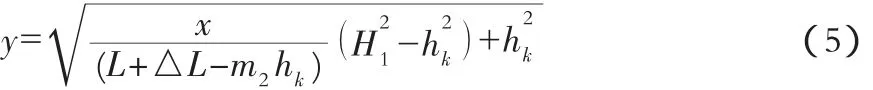
式中：H1为坝上游水深；H2为下游水深；m1为上游边坡；m2为下游边坡；k为坝体渗透系数；ΔL为等效矩形宽度；L为上游水位坝坡交点和下游坝坡与坝基交点的距离；hk为出水点水深；a0为逸出点水位以上的高度；q上游为坝体上游段单宽流量；q下游为坝体下游段单宽流量。

根据通过上下游段的单宽流量相等，由公式（1）、（2）、（3）、（4）联立导出：

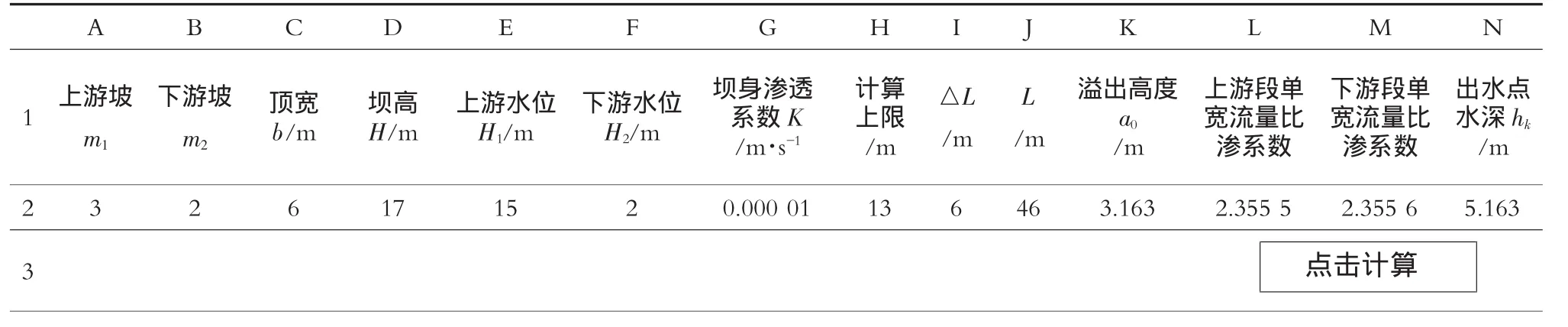
表1 迭代计算表

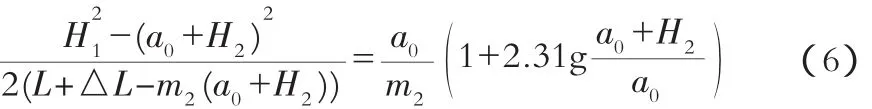
可以看出，公式（6）的两侧为关于a0的高次非线性方程，用一般纯数学的解析方法是难以求解的。而Excel的VBA程序恰好能够实现这一功能。据此，运用VBA编制程序计算可以在满足设计要求的前提下准确、高效地完成任务。

2 工程实例应用

吉林省某均质坝建于不透水地基上，坝高17 m，上游水深为15 m，下游水深为2 m，上游边坡为3，下游边坡为2，坝顶宽6 m，坝体土的渗透系数经实验测得为0.001 cm/s。要求：计算单宽流量并画出坝体内的浸润线曲线。

通过以上已知条件，把 H1，H2，m1，m2，K，b 带入公式（6）两侧，则左右分别为关于a0的表达式，只要计算出一个a0使左右两式的值相等，即为所求。根据a0的物理意义，取值范围为 a0∈[0，（H1-H2）]，给 a0赋予初始值（取 0.01），将分别得到公式（6）两侧的两个值，如果两值差的绝对值不满足要求（如大于0.000 1）,则继续给a0赋予新值，新值为原值基础上加一个微量（如0.001），重新计算，直到认为两值相等（即小于0.000 1），停止运算，此时a0的值即为所求。通过公式（4）的变形公式hk=a0+H2可求hk，在计算出hk后通过公式（5）则能求出浸润曲线方程。

3 VBA及其实现[1]

VBA是基于Microsoft Excel提供的IDE编程环境实现的一种自动化程序语言，通过在Excel的“宏”实现程序的自动化运行。在“工具”菜单下找到“宏”，点开“Visual Basic编辑器”，执行以下程序即可实现例题的求解结果。

将已知条件输入编好的电子表格中，按“点击计算”按钮再开始循环计算，直到L3和M3相等为止，a0，hk即为所求结果，如表1所示。

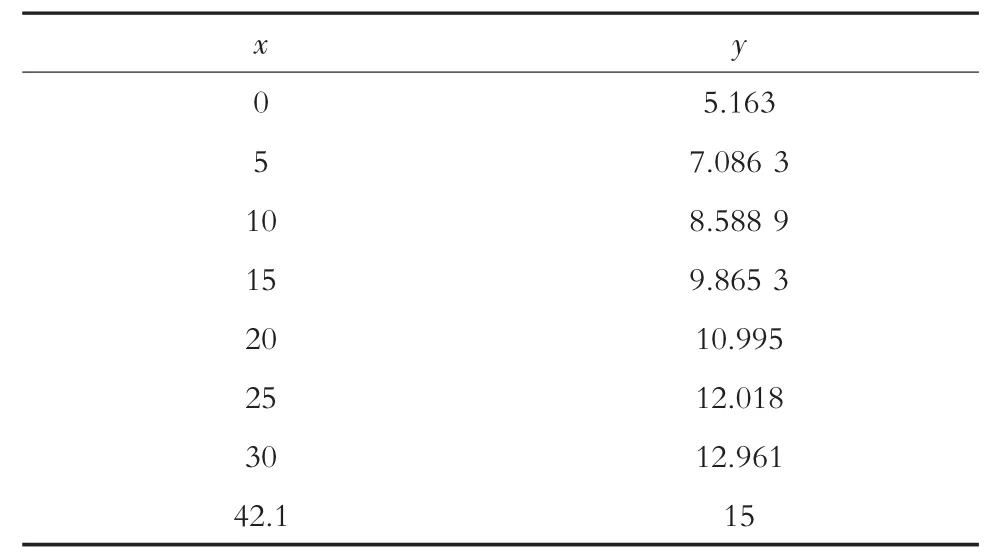
表2 浸润线坐标点计算

将hk值带入到公式（5）中，得下式：

根据 x 的取值范围[0，L+ΔL-m2·hk]，即[0，42.1]，计算出浸润线坐标点如表2所示。

按描点法绘出如图1中所示的浸润曲线，其上游段是从A′点开始的，而实际式（7）从A点渗入坝体，故需对前段A′F加以修正，采用近似方法把A点作为上游起点，与F点光滑连接。

4 结语

通过VBA在渗流计算中的应用，将复杂的试算过程用计算机程序来实现，省去了大量计算的工作时间和查表带来的误差以及人工试算的繁杂过程，并通过在Excel表格中的可视化做到了输入、输出格式直观方便，大大提高了准确率和工作效率。此方法适合大部分含有复杂试算过程的工程计算，比如溢流坝下游收缩水深，明渠均匀流正常水深及临界水深、消力池收缩水深等，供参考使用。

[1]神龙工作室编著.Excel高效办公：VBA范例应用[M].北京：人民邮电出版社，2006.

[2]李炜主编.水力学计算手册(第二版)[M].北京：中国水利水电出版社，2006.