基于WSN的CRC算法的改进与实现

李冠楠 李强

（顺德职业技术学院 电子与信息工程系，广东 顺德 528300）

1.CRC算法介绍

CRC校验采用多项式编码方法。利用生成多项式为k个数据位产生r个校验位进行编码，其编码长度为n=k+r，所以又称为（n，k）码。其编码格式如下：

1.1 编码规则[1]

设有k个数据位，需要添加r个校验位，n=k+r，其编码规则如下：

用W(x)=W W…W表示k个数据位，把W(x)左移r位，即相当于W(x)×2，给校验位空出r位来；

给定一个r阶的多项式E(x)，可以求出一个校验位表达式F(x)。E(x)称为该循环码的生成多项式。即如下表达式：

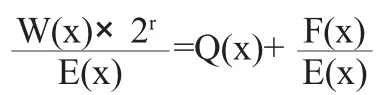
根据上面公式可知，用W(x)去除生成多项式G(x)，商为H(x)，余数则为R(x)。据此可得：

在CRC编码过程中，四则运算采用模2运算，即不考虑借位和进位。所以有：

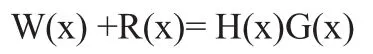
M(x)+R(x)即为所求n位CRC码，它应是生成多项式G(x)的倍式，即可以被G(x)整除。

校验数据时用数据的n位CRC编码去除G(x)，若余数为0则说明数据正确，否则根据余数的值即可查出差错位。

1.2 生成多项式特点

生成多项式应满足以下条件：

（1）任何一位发生错误，W(x)×2+R(x)即CRC码除以G(x)的余数不能为0；

（2）余数继续作模2除，应使余数循环；

（3）若要能纠正一位错，则不同的码位错不能有相同的余数，且当给定生成多项式后，余数与出错位之间的对应关系应保持不变，与编码无关。

1.3 原算法实现[2]

/*以CRC-CCITT为例，按位计算CRC算法实现，不使用额外空间*/

从上述代码可知，直接基于问题的描述和所涉及的概念出发，利用按位计算CRC，虽然代码简单（也可采用模拟硬件电路按位操作加以实现），所占用的内存比较少，但其最大的缺点就是一位一位地计算会占用很多的处理器处理时间，尤其在高速通讯的场合，这个缺点更是不可容忍，因而实现对它的改进具有理论和实际的意义。

2.CRC算法改进

2.1 快速算法基本思想[3]

CRC常用的生成多项式如 CRC-16、CRC-CCITT和CRC-32，由它们产生的校验码字节数均为整数个字节。而单片机的操作是以字节形式进行的，所以，算法应以字节为单位进行运算。显然，单片机的数据序列、校验序列都是字节序列。实际上，这种算法所要解决的问题就是如何对多字节序列进行除法取余式运算的问题，从而达到时空的权衡。

2.2 多字节序列运算规律

设一个由i个字节构成的字节序列Wi=[w1w2……wi-1wi]，取其前i-1个字节构成一个新的序列Wi-1=[w1w2……wi-2wi-1]，则两个序列之间的关系可以用多项式表示为Wi(x)=x8Wi-1(x)+mi(x)。

其中，mi(x)表示mi的二进制多项式形式，x8Wi-1(x)表示将Wi-1左移一个字节。

对于序列Wi-1来说，

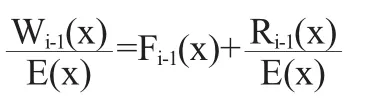
其中令二字节序列余数Ri-1=[hi-1li-1]

而对于序列Wi来说，可得

因此，对x8Ri-1（x）+wi(x)取余式运算就等价于对Wi(x)的取余式运算，即

其中，x8Ri-1（x）+wi(x)表示一个由Ri-1和mi共同组成的三字节序列[hi-1li-1wi]，故对它取余式运算就等于对Mi序列的取余式运算，其结果就是Mi序列的余式Ri=[hili]。故以此类推便可得到最终结果。

2.3 变字节序列的计算

为了时空的权衡我们在此引入了查表的思想，对于三字节序列如果事先计算出一字节即0x00至0xFF之间的所有的余式并汇制成表，这样就减少了时间开销且只需占用512个字节空间。

设三字节序列Tabc=[abc]、Ta00=[a00]和二字节序列Tbc=[bc]。用多项式表示为Tabc(x)=Ta00(x)+Tbc(x)。

对于序列Ta00来说，

而对于序列Tabc来说，可得

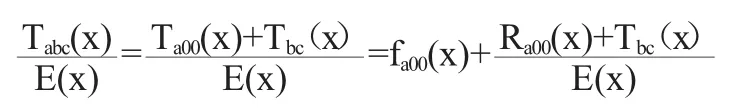
其中，Ra00和Tbc都是二字节序列，因此Ra00(x)+Tbc（x）仍然是二字节序列，它是Tabc的余数Rabc，即

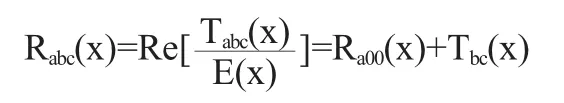
故三字节序列Tabc可分解为两个步骤进行计算：

通过查表，获取Ta00=[a00]的余式Ra00=[ha00la00]

计算 Rabc=[habclabc]，其中 habc=ha00⊕b，labc=la00⊕c

很显然，对于三字节序列只需建立一字节即0x00到0xFF的余式表，即按字节求CRC的思想，由于采用了查表法，大大提高了计算速度。但对于广泛运用的8位微处理器，代码空间有限，对于要求256个CRC余式表（共512字节的内存）已经显得捉襟见肘了，但CRC的计算速度又不可以太慢，故同理我们可以引入按半字节计算CRC的算法。

3.改进算法实现

在以上CRC原算法和改进算法的基础上，本文采用C51编码实现了CRC改进型数据校验算法，并对各改进方案进行了效率分析。

经过上述分析，无论是按字节还是半字节来计算CRC都采用了一种递推的思想。一种由小及大，利用一个问题给定实例的解和同样问题较小实例的解之间的关系建立起原问题的解。这一算法是基于递推运算的规律，并且每一次递推运算都是对一个三字节序列的计算（如图1所示）。

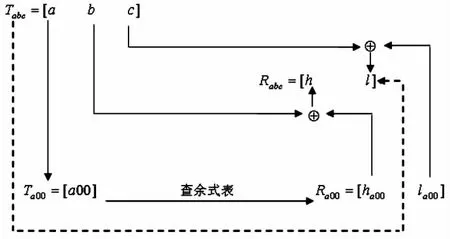
图1 三字节序列[abc]计算流程

4.算法效率分析

一个新算法的提出或改进是为了追求更高的效率，而对一个算法好坏的衡量除了最起码的正确性、易理解性外，其占用的存储空间和运算时间也是重要的标准。下面给出了以上三种计算CRC算法在相同条件、相同问题规模下的实验数据。以下为相关说明：

（1）按位计算

—按位计算CRC算法（b_CRC）

— 执行时间（b_CRC_t）：-ms

—额外空间：0Byte（恒定）

（2）按字节计算

—按字节计算CRC算法（B_CRC）

— 执行时间（B_CRC_t）：-ms

—额外空间：512Byte（恒定）

（3）按半字节计算

—按半字节计算CRC算法（HB_CRC）

— 执行时间（HB_CRC_t）：-ms

—额外空间：32Byte（恒定）

表1列出了三种计算CRC算法的对比（对应图2）。

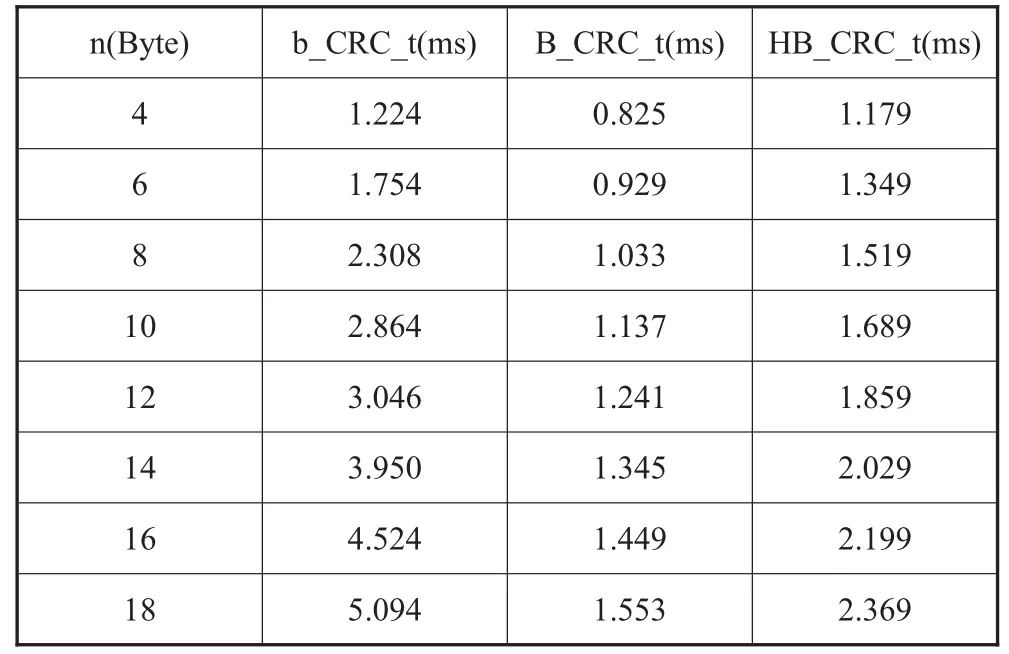
表1 三种计算CRC算法对比表

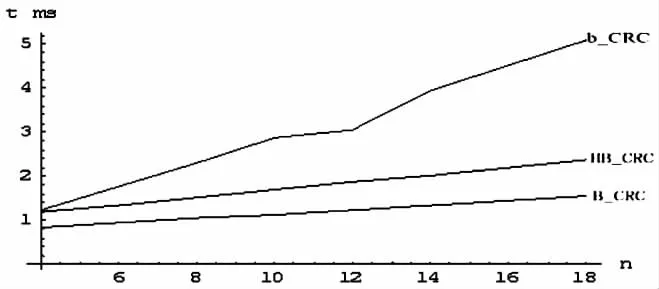
图2 CRC算法效率分析

通过对改进算法的编码实现，并在大量调试、统计和比较的基础上，我们可以得出以下结论：以上介绍的三种求CRC的程序，按位求法速度较慢，但占用最小的内存空间；按字节查表求CRC的方法速度较快，但占用较大的内存；按半字节查表求CRC的方法是前两者的均衡，即不会占用太多的内存，同时速度又不至于太慢，比较适合8位小内存的单片机的应用场合。

可见，以上几种算法从按位计算CRC的思想出发，并结合模2运算规则，在蛮力法的基础上提出了按字节、半字节计算CRC的改进策略，也就是从减治和时空权衡的角度进行问题的诠释，以一种空间换时间的思想实现了对原问题的快速、高效求解，从而满足无线MESH网络内节点的通信要求。

[1]王春森.程序员教程[M].北京：清华大学出版社,2002：75-93.

[2]W.Ye,J.Heidemann,D.Estrin.An energy-efficient MAC protocol for wireless sensor networks[J].The 21st Int'l Annual Joint Conf.on the IEEE Computer and Communications Societies(INFOCOM 2002).New York,USA,2002：1-10.

[3]常晓明.CRC校验及其软件实现[J].电子技术应用,1995(6)：67-71.