动态多模网络中演化社区发现算法改进

胡 昊，张小燕，苏 勇

（江苏科技大学 计算机科学与工程学院，江苏 镇江212003）

当今网络拥有海量数据，要从海量数据中得到有用的信息是很困难的，因此网络分析[1]和建模[2]受到越来越多的关注。目前很多研究工作都只涉及一种模式的网络，即网络中只存在一种类型的参与者（点），参与者之间只存在同种类型的关系（联系）。但是，最近迅猛发展的Web数据挖掘涉及到了不止一种类型的参与者，这些参与者之间的关系也不再仅限于一种。这种类型的网络称为多模网络[3]。

在多模网络中，不同模中点的进化是不相同的。对于具有动态关系的异构实体，发现演化社区有很多的好处：(1)能够清晰地了解迥异模式之间的联系和长期演化模式；(2)可以形象化具有多种实体和多种关系的复杂网络；(3)有助于在多种领域中做决策；(4)在早期如果发现不良的演化样式，也可以发出事件警告。

在动态多模网络中发现社区演化还是很困难的，原因有二：(1)不同的模式之间的演化是有关联的；(2)不同模式具有独特的演化样式。本文采用谱聚类架构，提出一种发现动态多模网络中演化社区的一般方法。一个动态多模网络会包含一系列的网络快照，利用这些快照可以找出社区是如何演化的。在这个模型下，加入正则项反映时态变化[4]，可以将有联系模式的聚类结果和相邻时间戳作为一个模式下的社区更新的属性，是一个将动态多模网络分析和常规的基于属性的数据挖掘联系起来的新方法。

1 问题阐述

给出含有 m种类型元素X1，X2，…，Xm的m模网络，找出每一模中的潜在社区是如何演化的[5]。在架构中，通过一系列的网络快照只关注离散时间戳，这个方法在正则项网络分析中得到广泛应用。表1所示为下文中所涉符号及其表示的内容。

1.1 使用网络序列发现社区

在动态多模网络中，有多种多样的网络快照。不考虑时态效应的目标函数F1可以写为：

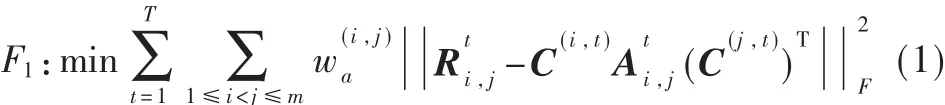
表1 符号及其表示的内容

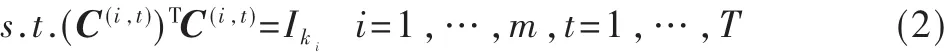
有如下定理：

定理 1： 如果 C(i，t)，1≤i≤m，1≤t≤T 是方程 F1的有效解，那么(i，t)也是具有相同目标值的有效解，其中(i，t)定 义 如 下 ：

1.2 使用时态正则化发现社区

公式F1并没有关注连续时间戳之间的关系。可以将F1归结为每一个快照单独地进行聚类。实际生活中的社区演化是非常缓慢的，为了得到平滑的社区演化，将增加时态正则项Ω，它可以迫使聚类序列通过不同的时间戳时变得平滑。

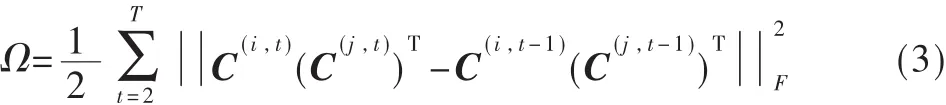
式(3)中，“1/2”只是为了下面求导方便做的计数。实际上，这里进行一阶马尔科夫假设，要求当前的聚类与前一个时间戳的聚类很相似。

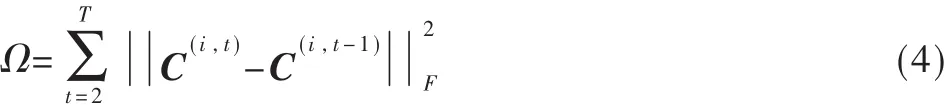
正如定理 1指出的，C(i，t)在正交变换下是相等的，因 此 ， 可 以 在 式(4)中 直 接 比 较 C(i，t)和 C(i，t-1)， 而 不 必 得出它们在不同时间戳下聚类指示符的不同。相比较而言，式(3)中正则项与正交变换无关，因此应该得到相邻时间戳下社区结构的不同。因为正则化，发现演化社区的问题就可以阐述成：

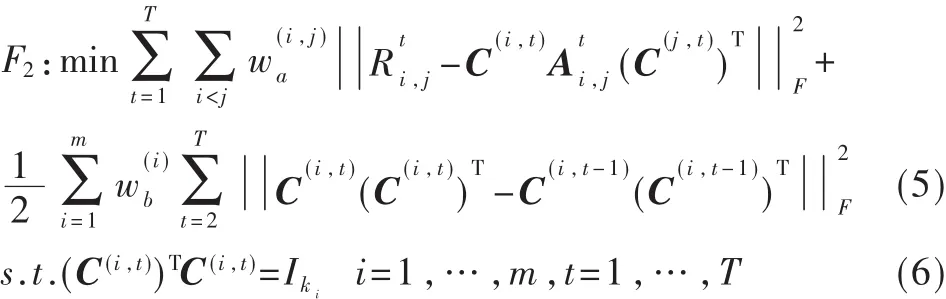
2 时态正则化多模聚类

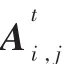
2.1 A的估计

定理 2：对于给定的 C(i，t)，最佳的社区作用矩阵可以使用下式得到：

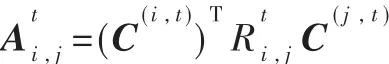
2.2 C的计算

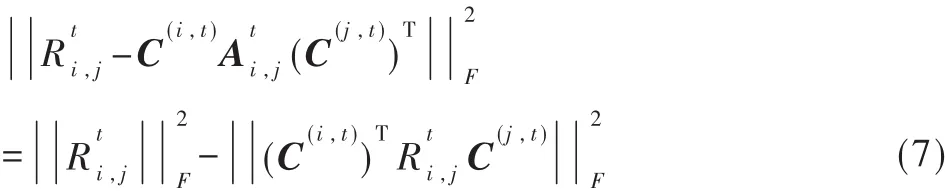
同时：

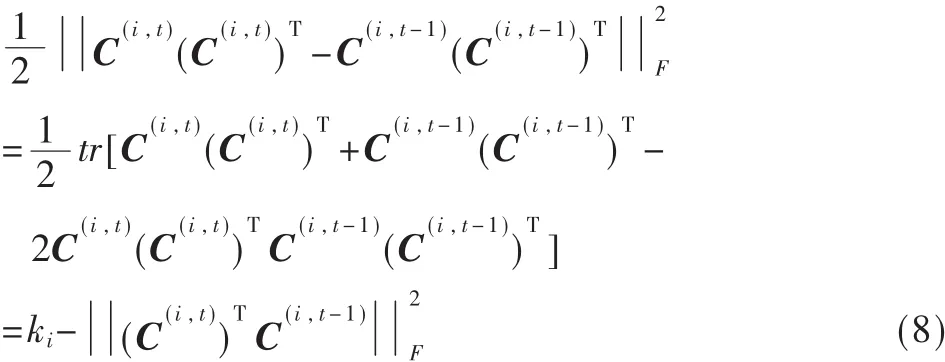
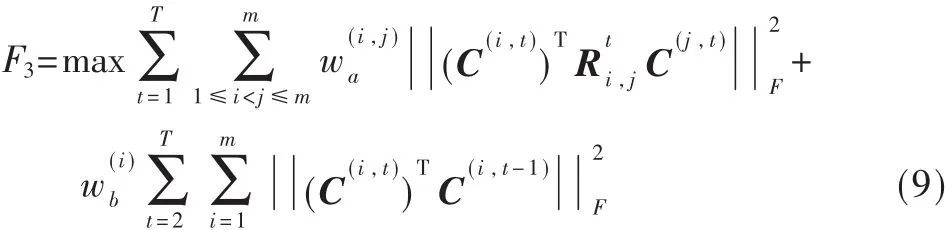
注 意 ，C(i，t)、C(j，t)以 及 C(i，t-1)都 是 有 联 系 的 。 一 般 来说，这个函数没有解析的闭合形式解。但是如果有给定的C(j，t)和 C(i，t±1)，则 可 以 根 据 定 理 3 直 接 得 到 最 佳 的 C(i，t)。

定 理 3： 如 果 给 定 C(j，t)和 C(i，t±1)， 那 么 C(i，t)就 可 以作为矩阵的顶左奇异向量求解，通过以下矩阵在列方向的级联得到。

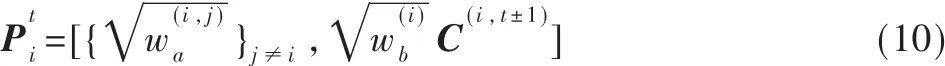
2.3 属性视图中的算法

借助轮换寻优思想解决式(9)中的F3问题。即求解C(i，t)时，固定其他变量的值。这个过程一直迭代，直到函数收敛。收敛之后，{C(i，t)}就是近似的社区指示符矩阵。通常使用后处理视图恢复社区中不相邻部分，即对社区指示符采用k-均值聚类。综上所述，时态正则化多模聚类算法如下：

在属性视图中解释这个算法，更新C(i，t)的每一步都和潜在的语义分析过程一致。根据定理3，社区指示符和矩阵的左奇异向量是一致的，在式(10)中也做了定义。如果将作为正规实例-属性矩阵，则找出社区指示符和进行潜在的语义分析LSA(Latent Semantic Analysis)同样重要。图1指出了整个算法的过程。

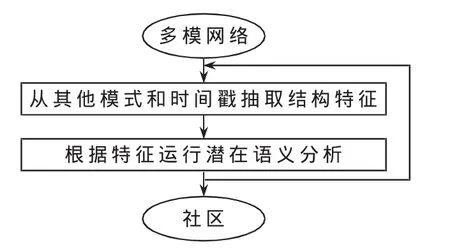
图1 树形视图中的算法：迭代的LSA

3 动态数据上的实验

实验中进行下面三种方法的比较：静态聚类、在线聚类和本文提出的时态正则化多模聚类。静态聚类是一种基线方法，它不关心任何的时态规则化。静态聚类通过对式(1)中的F1求解对每一个网络快照单独进行聚类。

因为真实的数据不包含验证信息，即在不同时间戳下的社区联系，因此，使用合成数据验证提出算法的有效性。

3.1 实验设置

构建一个三模动态网络，模分别有2、3、4个社区和50、100、200个元素。每两个模型之间都可以发生联系，为了产生迭代，条件设置为：(1)为每个元素决定潜在的社区；(2)实体之间基于团体同一性产生的关系符合伯努利分布。

为了模拟演化，在不同的时间戳下按照如下规则发生联系：

(1)在每个时间戳下，参与者的部分(20%～50%)要转化为与先前时间戳下的组完全不同的组中，这是为了模拟社区演化。

(2)两个组之间发生联系的概率是高斯分布的样本，主要和先前时间戳下的概率有关。这是为了模拟联系的改变。

(3)在每个时间戳下添加噪音。例如噪音强度是0.2，则联系矩阵中大概有20%的词条被随机设为0，另外20%的词条被随机设为1。噪音和潜在的组结构是独立的，因此，噪音强度越高，在联系中的社区结构越不容易被发现。

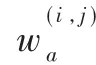
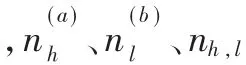
3.2 实验结果

表2列出了超过100次运行的结果取平均值，其中，粗体表示结果中最好的。从表中数据可见，聚类效果随着噪音的加强变得越来越坏。总体来看，规则化聚类比在线聚类的效果好，在线聚类比静态聚类的效果好。从结果中也注意到，当噪音强度比较大（即噪音强度为0.55）时，社区结构的平滑性遭到了破坏，也因此时态正则化聚类效果比静态聚类还差。

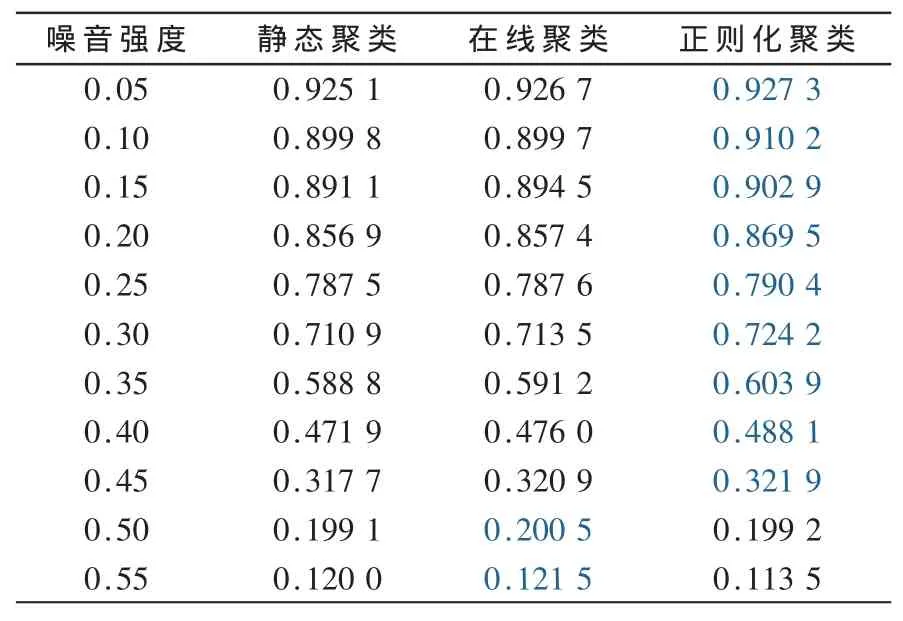
表2 不同噪音强度下各种聚类比较

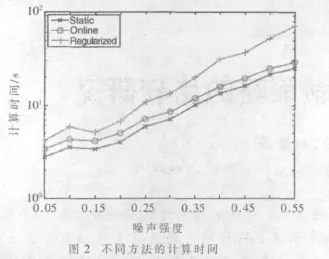
图2显示平均计算时间。噪音越大，计算时间越长。静态聚类需要的时间是最短的，在线聚类的时间相对较长，时态正则化聚类的时间是最长的，特别是当噪音强度非常大时，时间变得不可接受。在这种情况下，时态平滑性已经被损害，算法需要更多的迭代找到最优解。

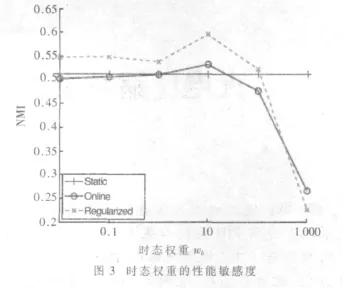
为了显示参数调整的效果，选择中等噪音强度的数据集，使用在线聚类和正则化聚类，时态权重wb从0.01～1 000进行调整，wa固定为 1。如图3所示，时态权重过大反而得到不好的效果，即时态正则化处于首要地位。大部分时间，时态规则化有利于聚类考虑时态信息，时态权重在0.01～100的范围内体现的尤为明显。

在实际应用中，异构参与者之间的互相作用形成了多模网络。正是在这样的网络中，不同模的参与者构成社区并慢慢演化。本文提出了时态正则化多模聚类算法在动态多模网络中发现演化社区。这个算法可以理解为迭代的LSA过程，在不同模和时间戳下的属性构成社区矩阵。基于这种属性视图，提出的算法也能扩展到处理带有属性的网络、模内联系以及休眠点和活跃点。实验结果证明该算法能够根据一系列的快照找到更精确的社区结构和社区演化。

[1]NEWMAN M.The structure and function of complex networks[J].SIAM Review，2003，45(2)：167-256.

[2]CHAKRABARTI D，FALOUTSOS C.Graph mining：laws，generators，and algorithms[J].ACM Comput.Surv.，2006，38(1)：65-78.

[3]WASSERMAN S，FAUST K.Social network analysis：methods and applications[M].Cambridge University Press，1994.

[4]BAUMES J，GOLDBERG M，WALLACE W，et al.Discover-ing hidden groups in communication networks[C].In 2nd NSF/NIJ Symposium on intelligence and Security Informatics，2004.

[5]LONG B，ZHANG Z M，WU X，et al.Spectral clustering for multi-type relational data[C].In ICML’06：Proceedings of the 23rd international conference on Machine learning.ACM，2006：585-592.

[6]王林，戴冠中.基于复杂网络中社区结构的论坛热点主题发现[J].计算机工程，2008，34(11)：214-21.