改进的货运量最优变权组合预测模型*

谭司庭，史 峰

(1.中南大学物理科学与技术学院，湖南 长沙 410083;2.中南大学交通运输工程学院，湖南 长沙 410075)

一个地区的货运量，是最重要的经济指标之一，直接表明了该地区的经济活跃程度。科学准确地对货运量进行预测，是运输业持续健康发展的有效保障，是运输各级决策部门制定发展战略和规划的重要依据。人们往往习惯用某个模型对货运量进行预测［1－2］，但这些方法由于各自的局限性，常常预测精度不高。为了综合利用现有的预测方法所提供的信息，尽可能地提高预测精度，许多人采用组合预测方法对货运量进行预测［3－4］。J.M.Bates和C.W.J.Granger对组合预测进行了系统研究［5］。唐小我［6］等研究了基于定权组合预测问题，取得良好的效果。但它允许负权重因子的存在，物理意义不明显。许多学者对非负权组合做了大量的研究［7－8］，主要集中变权组合的研究［9－11］，如何提高预测精度。

在实践中发现，变权组合预测方法对1个计划年度内的短期预测有较好的预测精度，但对于5年以上的长期预测，其预测误差非常大。因此，本文提出新的变权组合预测模型，在进行长期预测时，增加收敛条件，使变权的优势在长期预测中也能体现。根据实际数据进行计算表明，本方法在短期预测与长期预测中均能取得良好效果。

1 改进的变权组合预测模型

设n个时刻原始数据序列为x(t)，t=1，2，…，n。m个预测模型在t时刻预测值为fi(t)，i=1，2，..，m;t=1，2，..，n。在 t时刻变权的组合预测值为

式中，gi(t)为第i个模型在t时刻的权重，满足:

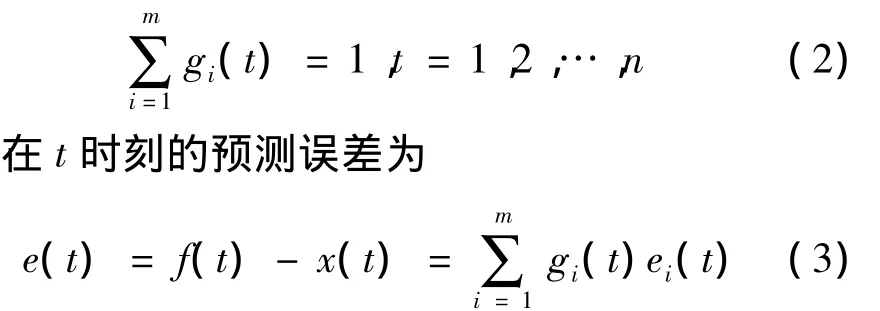
式中，ei(t)为第i个预测模型的预测值在t时刻的误差。

变权组合预测模型就是利用m个预测模型的预测值确定前n个时刻的权重值，再预测某个时刻的权重值gi(t)，从而得到该时刻的预测值。对gi(t)的预测，可以设定其函数形式，在此设为p次多项式形式:

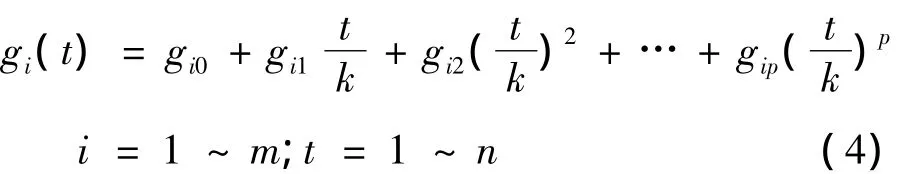
式中，k表示预测到未来某个时刻，且k≥n。

对条件(2)，由于要任意t都成立，故:

最优变权组合模型:满足(10)和(11)式。

由于该模型有可能让变权系数为负值，使权重因子的意义不明确，故非负权组合预测模型一般会增加 1 个条件［7－8］:

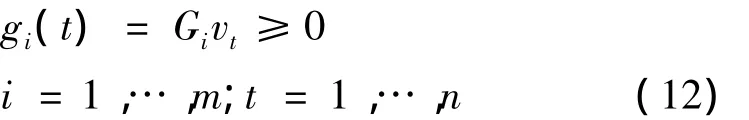
因此，最优非负变权组合模型满足(10)～(12)式。

但是，这种非负权组合由于在求解系数矩阵时，非线性方程组呈病态，故在长期预测时，由于积累误差，计算会发散，预测误差也非常大，特别是多项式阶数p取3以上更明显。使用多项式作为预测的权重函数，就是用多项式去逼近真实的函数。这种逼近的方法，必须满足收敛的条件。可以新增条件:

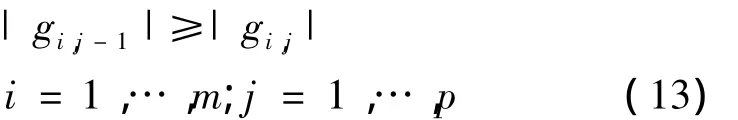
使多项式在k的时间内收敛。

因此，在进行长期预测时，增加公式(13)的收敛条件，会减少发散的危险，即由式(10)～(13)式构成了带收敛条件的最优变权组合预测模型;在进行短期预测时，则由式(10)～(12)构成最优变权组合预测模型。

2 权重矩阵G的求解算法

利用拉格朗日求极值法，求解最优变权组合模型:

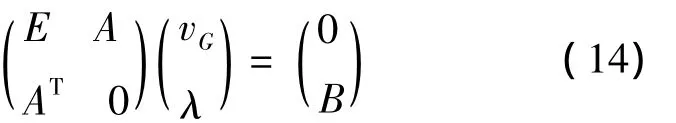
为了求解带收敛条件的最优变权组合预测模型，将条件(13)写成如下形式:

利用拉格朗日求极值法可以求出权重系数gi，j。令

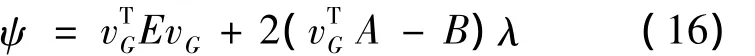
对变量 gi0，φij，λi的偏导为零得到:

解上述非线性方程组即可得到权重矩阵G。事实上，上述非线性方程组是一个病态方程组，用一般的非线性方程组的方法无法求得正确解。

令ξ=EvG+Aλ。如果存在vG满足ξ=0，方程(17)就能满足，此时的解就是最优变权组合的解。如果由于条件(13)的限制，不能满足ξ=0，可令相应项的 cosφij=0，sinφi，j= ± 1，gi，j= ± gi，j－1，则相应Ci中的j+1行为零，如果存在vG满足ξ中除gij对应的分量ξi·m+j外，其他分量为零，方程(17)仍然能满足;如果不能满足继续令相应项的cosφij=0，直到满足为止。

对于 gi，j= ± gi，j－1的正负号的取定也不是随意的，它可能让方程不满足ATvG－B≠0;也有可能出现0=0的情况。为了顺利解出方程，给出如下算法:

(1)给定定权的minJ和相应的vG。

(3)如果ηij=0保持变量gij，否则将矩阵E的第(i－1)(p+1)+j行加上(i－1)(p+1)+j+1行与ηij的积，并将A做相应的变换。再将矩阵E的第(i－1)(p+1)+j列加上(i－1)(p+1)+j+1列与ηij的积。并去掉相应的第(i－1)(p+1)+j+1行、列以及相应的变量 gij，这样得到新的矩阵 E'，A'，v'G。

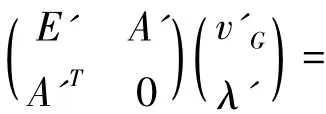
(6)改变η中非零项的正负号，尝试下一个可能的η。如果所有可能的尝试完毕，转第7步;否则转第3步。

(7)输出相应的vG。

3 实例分析

以长沙市的货运量为例，对上面算法进行实例分析。从1990～2008年的全社会固定资产投资、GDP总额、货运总量为长株潭原始数据。2009～2015年的全社会固定资产投资、GDP总额是通过指数外推得到的数据。通过这些原始数据对2015年长沙市的货运量进行预测。

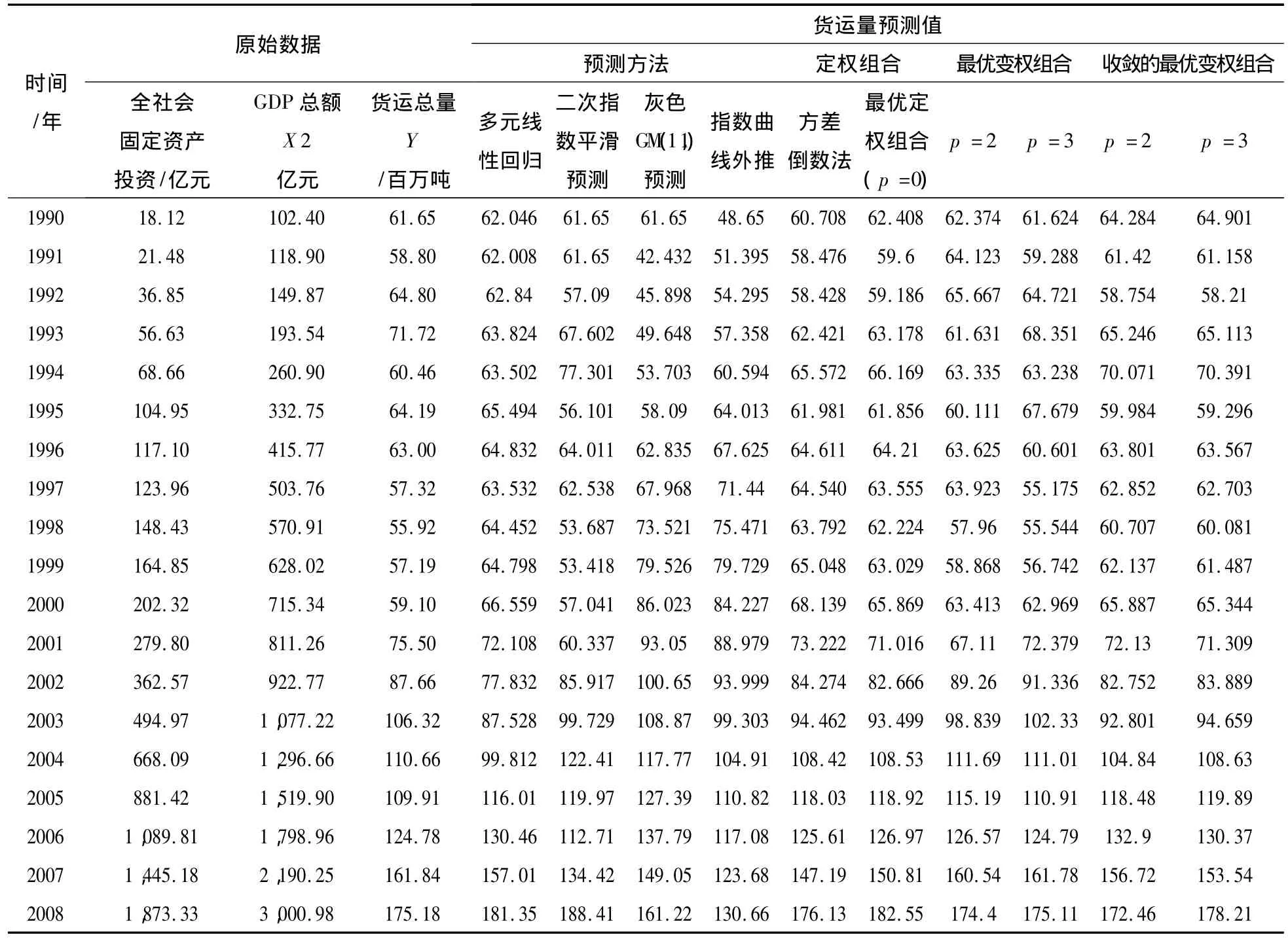
表1 原始数据及货运量预测数据Table 1 Original data and forecast data of freight volumes

(1)多元线性回归:以全社会固定资产投资(x1)、GDP总额(x2)为自变量，货运总量(y)为因变量，得到回归方程:

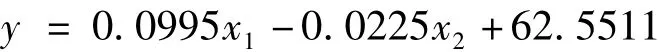
(2)二次指数平滑法:由于货运量数据有较明显的变动，因此取α =0.8。已知的数据个数n=19，故初值的选择对以后预测的影响不大，故选择第1期的数据作为初始值。

(3)灰色GM(1，1)模型预测:首先对货运量数据累加，再进行预测，得到预测方程为:

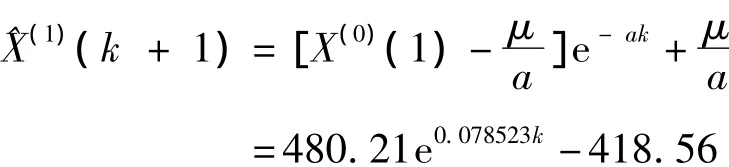
最后再累减得到预测数据见表1。

(4)指数曲线外推:利用指数曲线耦合得到预测方程:

(5)组合预测模型:利用前面4种预测方法进行组合预测，组合方法有方差倒数法、最优定权、最优变权、带收敛条件的最优变权组合预测，这些组合预测方法得到预测权重矩阵数据如表2所示。

表2 组合预测的权重系数矩阵Table 2 Weight coefficient matrix of combined forecast

采用滚动的方式，进行短期预测测试，即每次用前面若干个数据记录来预测下1个步长的数据，见表3。

表3显示各种预测方法的短期预测的误差。从表中可以看到，组合预测比单个预测误差小，变权预测组合比定权预测的误差小。在短期预测中，最优变权的预测效果最好，且随着预测函数的最高次数p的增加，预测精度逐步增加。

为了进行长期预测测试，利用1990年到2008年的数据，对2009－2015年的数据进行预测，预测结果如表4所示。

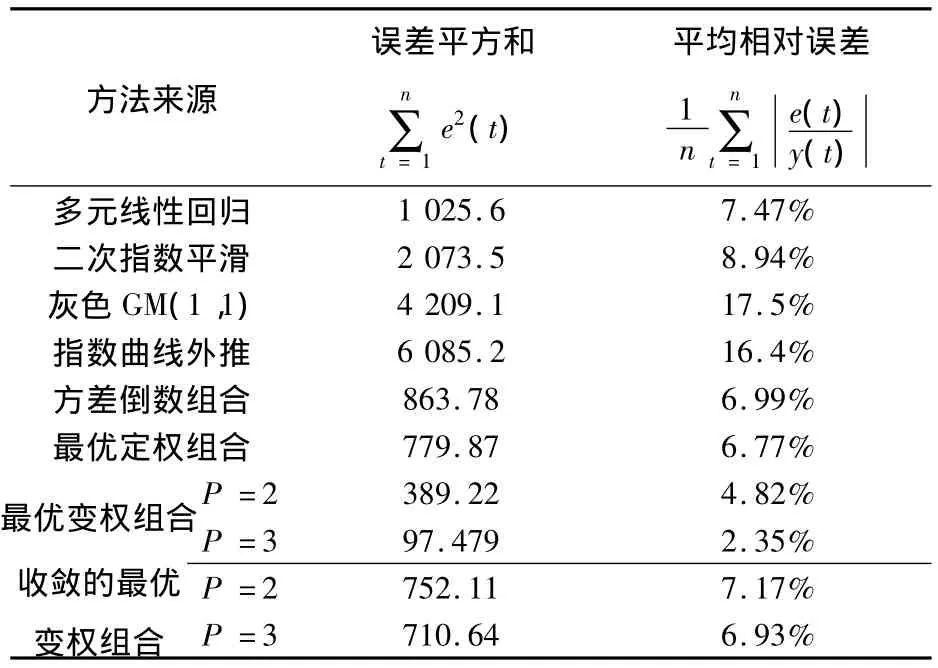
表3 短期预测误差比较Table 3 Comparison of short term forecast errors

对于未来的2015年，由于无法知道真实的货运量值，所以无法对其进行误差比较。对于同一种预测方法，p取不同值，只是预测精度不同，因此通过自身方法的预测值，p取不同值进行比较，可以反映数据可靠程度。表5中的F2，F3分别表示p=2，3时的预测值，表5显示了最优变权组合、带有收敛条件的最优变权组合2种方法对2015的货运量预测结果的比较，利用p取不同值的差别，比较2种方法的预测结果。收敛的最优变权组合的相对偏差达295%，可以明显看到最优变权组合预测方法的不可信。它的预测值与其他方法预测值也相差很多。而具有收敛性的最优变权模型，与其他方法并不大，自身比较也不大。可以看到，具有收敛性的最优变权模型同样适合长期预测，而最优变权组合预测不适合长期预测。而在短期预测中也有明显优势。

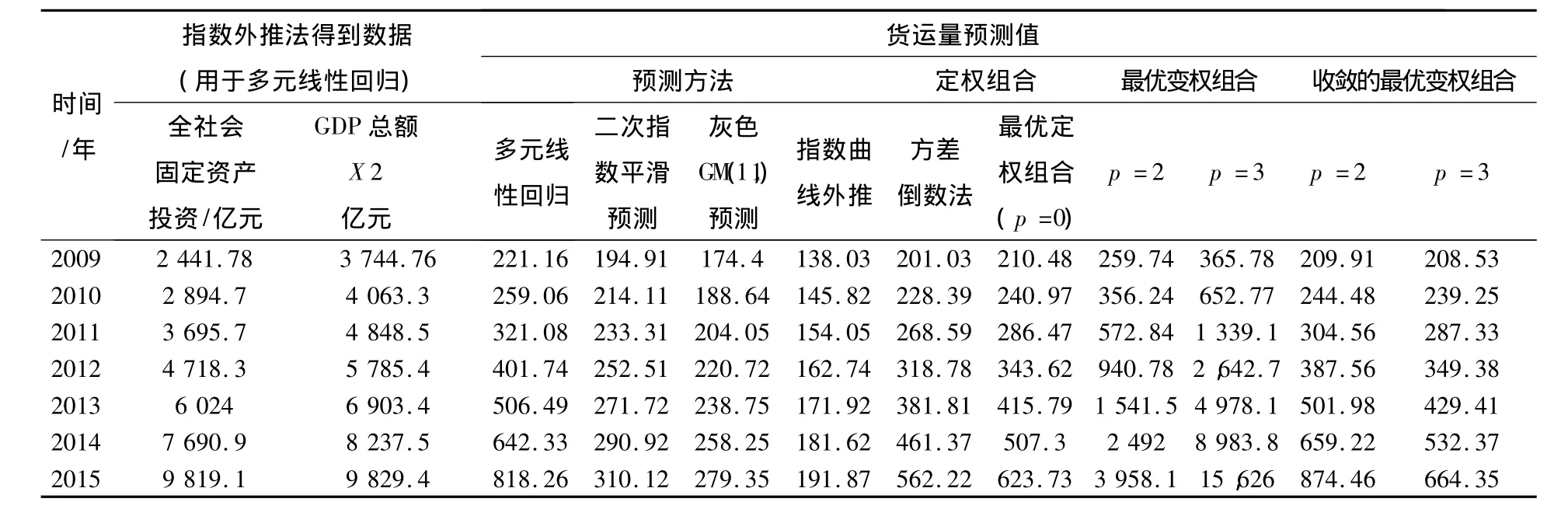
表4 2009～2015年的货运量预测值Table 4 Freight volumes forecast of 2009～2015

事实上，最优变权模型就是利用短期误差平方和最小得到的结果，而在长期预测时，由于不满足收敛条件，使数据发散，模型不再适用。具有收敛性的最优变权模型正好弥补这一缺点。如果最优变权模型满足收敛条件时，最优变权模型与具有收敛性的最优变权模型结果是相同的。具有收敛性的最优变权模型无论何时都保证数据收敛，因此对长期预测同样适合。如果预测期加长，则限制更多，这样短期预测误差增大，但保证长期预测收敛，这样做是值得的。

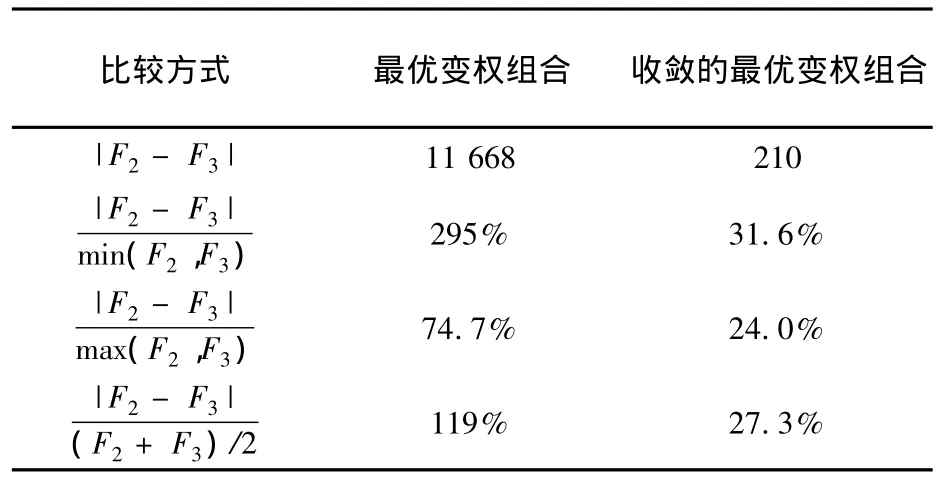
表5 2015年预测数据分析Table 5 Analysis of 2015 forecasts data

4 结论

(1)将具有多项式形式的变权函数的最优变权组合模型应用于长沙市的货运量的预测。发现该模型对短期预测，提高精度效果非常明显;在进行长期预测时，通过增加收敛条件，建立了带有收敛条件的最优变权模型。通过引入松弛函数，对求解过程做出理论分析，给出了具体算法。算法避免了病态非线性方程的计算。

(2)通过具有收敛性的最优变权模型与最优变权模型比较，发现带有收敛条件的最优变权模型在长期预测的效果非常理想，在短期预测时采用不带收敛条件的最优变权组合预测模型，利用这2个模型在不同条件下分别工作，取得不错的效果。

［1］缪 岩.GM(1，2)模型在内河货运量预测中的应用［J］.现代交通技术，2008，5(1):84 －86.MIU Yan.Application of GM(1，2)in the forecast of transport volume of inland river［J］.Modern Transportation Technology，2008，5(1):84 －86.

［2］赵卫艳.线性回归模型在货运量预测中的应用［J］.山西建筑，2007，33(9):248－249.ZHAO Wei-yan.The applying of line model in transportation forecast［J］.Shanxi Architecture，2007，33(9):248－249.

［3］吴晓玲，符 卓，王 璇，等.铁路货运量组合预测方法［J］.铁道科学与工程学报，2009，16(5):89 －92.WU Xiao-ling，FU Zhuo，WANG Xuan，et al.Combine forecast method for railway freight volum［J］.Journal of Railway Science and Engineering，2009，16(5):89 －92.

［4］杨鹏程，龙建成，马建军.铁路货运量的组合预测方法研究［J］.物流科技，2006，29(11):66－68.YANG Peng-cheng，LONG Jian-cheng，MA Jian-jun.The study of combine－forecast method for railway freight volumes［J］.Logistics Sci－ Tech，2006，29(11):66 －68.

［5］王 景，刘良栋，王作义.组合预测方法的现状和发展［J］.预测，1997(6):37 －38.WANG Jing，LIU Liang-dong，WANG Zuo-yi.The present status and developmentof combination forecasting method［J］.Forecasting，1997(6):37 －38.

［6］唐小我.最优组合预测方法及其应用［J］.数理统计与管理，1995，11(3):31 －35.TANG Xiao-wo.The optimal combination forecast method and its application［J］.Application of Statistics and Management，1995，11(3):31 －35.

［7］杨桂元，唐小我，马永开.关于非负权组合预测的若干问题的探讨［J］.电子科技大学学报，1996，25(2):210－215.YANG Gui-Yuan，TANG Xiao-wo，MA Yong － kai.Research on several problems for combined prediction of non－ negative weight［J］.Journal of UEST of China，1996，25(2):210－215.

［8］曾 勇，唐小我，曹长修.非负权重最优组合预测方法研究［J］.管理工程学报，1995，9(3):153 －160.ZEN Yong，TANG Xiao-wo，CAO Chang-xiu.A study of optional combination forecasting methods of non－negative weights［J］.Journal of Industrial Engineering/Engineering Management，1995，9(3):153 － 160.

［9］周传世，刘永清.变权重组合预测模型的研究［J］.预测，1995，14(4):47 －48.ZHOU Chuan-shi，LIU Yong-qing.A study of variable weighting combination forecast model［J］.Forecasting，1995，14(4):47 －48.

［10］曹长修，王 景，唐小我.一种模糊变权重组合预测方法 －FVW法的研究［J］.预测，1996(5):49－50.CAO Chang-xiu，WANG Jing，TANG Xiao-wo.A fuzzy variable weighting algorithm for combination forecastingresearch of FVW［J］.Forecasting，1996(5):49 －50.

［11］谢开贵，周家启.变权组合预测模型研究［J］.系统工程理论与实践，2000(7):36－40.XIE Kai-gui，ZHOU Jia-qi. Research of the weight changeable combination forecast model［J］.Systems Engineering Theory＆ Practice，2000(7):36－40.