钢筋混凝土压弯剪扭构件抗扭刚度探讨*

任文锋，李 芳

(1.中南大学 土木工程学院，湖南 长沙 410075;2.长沙铁路勘察设计有限公司，湖南 长沙 410001)

地震时候地面不但有平动，而且有转动，因此，高层建筑结构在地震作用下不仅有平移，还会有绕刚度中心的扭转。震害分析表明，扭转是一个很重要的致坏因素［1－2］，当高层建筑结构平面布置不对称时，扭转效应更为明显，因此现行高规增加了对结构偏心扭转的限制［3］。现有的矩阵位移法与近似计算法等结构扭转计算方法［4］均未深入构件层次，未考虑构件开裂后抗扭刚度的降低，然而，随着结构扭转幅度的增大，处于压弯剪扭复杂应力状态下的构件抗扭刚度会不断退化，可能导致扭转效应增大，从而加剧结构的破坏，因此压弯剪扭构件抗扭刚度是研究结构整体扭转性能的基础。

目前构件抗扭试验大都集中在承载力方面［5－9］，建立了一系列强度相关方程，而对构件的抗扭刚度关注较少;刘继明等［10－12］基于空间变角桁架模型，利用虚功原理推导了压弯剪扭构件的抗扭刚度，但计算公式比较复杂，不便于应用。本文在已有试验的基础上，给出了便于查用的构件抗扭刚度－扭转角退化曲线;通过对试验数据及抗扭刚度计算公式的参数分析，探讨了轴压比、偏心距、纵横钢筋配筋强度比、剪扭比及弯扭比等诸多因素对构件抗扭刚度的影响。

1 抗扭刚度总体退化规律

1.1 构件初始扭转角

构件开裂前，在复杂应力作用下，其内部已有部分裂缝开展［10］，构件初始抗扭刚度约为弹性抗扭刚度的0.8倍，即

式中:G为混凝土的剪切模量，取G=0.4E，E为混凝土的弹性模量;截面的抗扭惯性矩It=αβ4;GIt称为构件的弹性抗扭刚度。

表1 矩形截面构件在扭转时的系数α，βTable 1 Torsion coefficients α，β of rectangular section

表中b，h分别为截面的短边与长边尺寸;对于狭长矩形截面(m ＞10时)，It=ht3/3，其中，t为截面厚度。

而构件开裂时的抗扭刚度为弹性抗扭刚度的0.44 倍，即

鉴于构件开裂前的塑性发展程度并不明显，可近似认为构件刚度与扭转角呈反比关系，由于构件开裂时的抗扭刚度是初始刚度的0.55倍(0.44/0.8=0.55)，故可认为构件的初始刚度对应的位移角θ0是构件开裂时的扭转角θcr的0.55倍，即θ0=0.55θcr。

钢筋混凝土复合受扭构件的开裂扭矩Tcr计算公式为［13］:

式中:系数K=1.76(1－fcu/60);Wt为抗扭截面弹性抵抗矩，Wt=βb3，β的取值见表1;ft为混凝土的抗拉强度设计值;N为构件承受的轴力;A为构件截面面积。

构件开裂时的扭转角为

于是，构件的初始刚度对应的位移角为

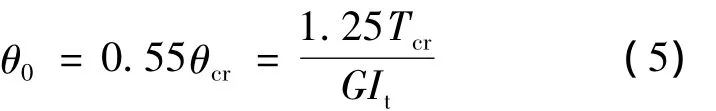
1.2 构件抗扭刚度总体退化规律

构件开裂后，抗扭刚度会随着扭转角的增大而不断降低。孙黄胜等［11］曾对9根截面尺寸为250 mm×250 mm的钢筋混凝土柱(740 mm长)进行抗震扭转性能试验，得到8根有效试件，将其退化系数加权平均可得到压弯剪扭构件抗扭刚度退化规律(见图1)。图中纵坐标为退化后的割线刚度与初始刚度Kt0=0.8GIt的比值，横坐标为构件扭转角与初始刚度对应的位移角θ0的比值。

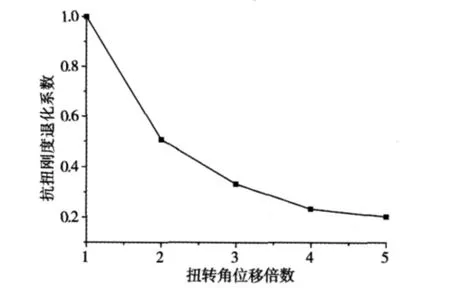
图1 抗扭刚度总体退化规律Fig.1 Total degradation graph of torsion stiffness

从图中可以看出，构件抗扭刚度起初退化严重，当构件扭转角为2倍初始刚度对应的位移角时，刚度退化50%;随着扭转角的进一步增大，退化幅度减少，最终稳定至0.2倍初始刚度左右。需要说明的是，图2是对试验数据做加权平均得到的，具有普遍性，能大致反映压弯剪扭构件刚度退化的规律。

2 抗扭刚度影响因素

高层建筑结构中的构件于压弯剪扭复杂应力状态下，国内外学者的大量试验研究表明:轴压力、弯矩、剪力的存在，对构件开裂前的扭转刚度的影响可以忽略不计。构件开裂后，抗扭刚度退化与纵筋和箍筋的配筋率、纵横钢筋配筋强度比、构件上作用荷载比例和截面尺寸有关［12］。为简便起见，本文通过试验数据的对比来分析轴压比、偏心距等因素的影响，对基于空间变角桁架模型推导的抗扭刚度计算公式进行参数分析，探讨纵横钢筋配筋强度比、剪扭比及弯扭比等影响因素。

图2为不同偏心距下轴压比对构件退化规律的影响，图3为不同轴压比下偏心距对抗扭刚度退化的影响。

图2 轴压比对抗扭刚度退化的影响Fig.2 Influence of ratio of axial compressive force to axial compressive ultimate capacity of section on torsion stiffness degradation

2.1 轴压比

从图中可以看出，在相同的偏心距下，构件的抗扭刚度退化随着轴压比的增大而加剧;当偏心距增大时，轴压比对构件抗扭刚度退化影响变小。

图3 偏心距对抗扭刚度退化的影响Fig.3 Influence of eccentricity on torsion stiffness degradation

2.2 偏心距

从图中可以看出，在小轴压比(0.2)情况下，偏心距对构件的抗扭刚度退化的影响较小。在大轴压比情况下，随着轴压比的增大，构件的抗扭刚度退化加剧。

2.3 纵横钢筋配筋强度比

研究表明，基于空间变角桁架模型，利用虚功原理推导的压弯剪扭构件的抗扭刚度计算公式［12］，公式大体有3项，一次反映了纵筋、箍筋与混凝土对构件抗扭刚度的贡献，概念清晰，且与试验结果复合良好，但比较复杂，不便于应用。

式中:b0=b－as;h0=h－as;b，h分别为截面宽度与高度;as为受拉区边缘到受拉钢筋合力作用点的距离;u0=2(b0+h0);ζ=(fyAs+N)s/AsvTfyvu0;Es，Esv分别为纵向钢筋、箍筋的弹性模量;ψ =M/T;M为构件所受的弯矩;N为构件所受的轴力;As，A's分别为截面全部受拉纵筋面积总和;η=Vb0/T;V，T为构件所受的剪力;s为箍筋间距;AsvT为箍筋截面面积;Ec为混凝土的弹性模量;t为变角空间桁架模型中箱形截面的壁厚，矩形截面取t=b/6，箱形截面时取b/6与截面实际壁厚的较小值。

现对该公式进行纵横钢筋配筋强度比ζ、剪扭比η及弯扭比ψ等参数分析，探讨其对构件抗扭刚度的影响。由于式(6)变量较多，此处假定b×h=700 mm×700 mm;纵筋采用HRB400钢筋，As=A's=700 mm2;箍筋采用HPB253钢筋，间距s=150 mm;混凝土采用C30;剪扭比取 η =0.5。变化纵横钢筋配筋强度比ζ的取值，以ζ=1时的构件抗扭刚度为基准，可得纵横钢筋强度比对抗扭刚度的影响(见图4)。

图4 纵横钢筋强度比对抗扭刚度的影响Fig.4 Influence of intensity ratio of longitudinal steel to traverse steel on torsion stiffness

从图中可以看出，纵横钢筋强度比在1附近时，构件的抗扭刚度最大。

2.4 剪扭比

取纵横钢筋配筋强度比ζ=1，变化剪扭比η的取值，以纯扭(η=0即)时的构件抗扭刚度为基准，可得剪扭比η对抗扭刚度的影响(见图5)。

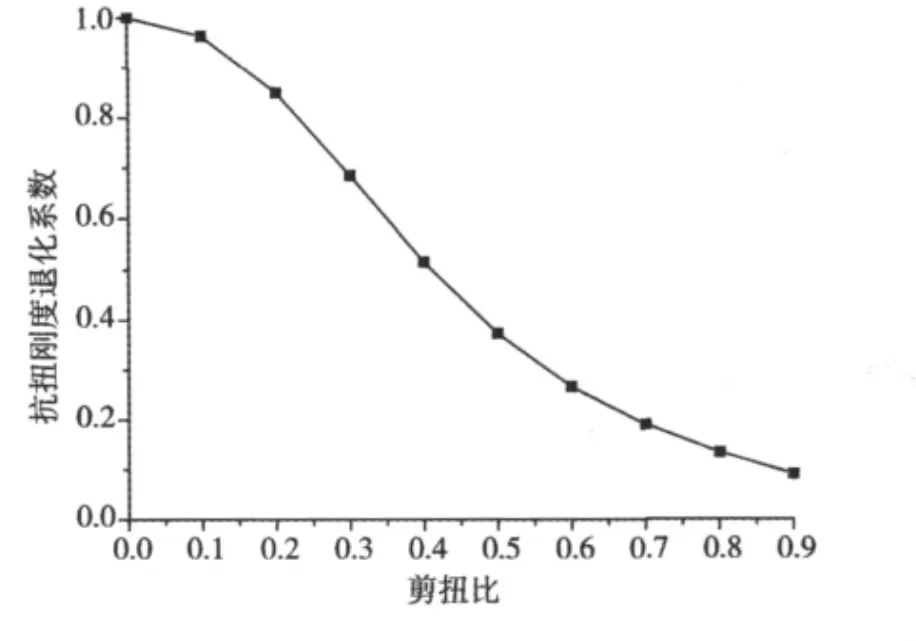
图5 剪扭比对抗扭刚度的影响Fig.5 Influence of ratio of shear to torsion on torsion stiffness

从图中可以看出，剪力的存在使得构件抗扭刚度降低，且随着剪扭比的增大而不断退化，当剪扭比为0.5时，构件抗扭刚度退化60%。

2.5 弯扭比

实际工程中，柱子配筋一般都是采用对称配筋(即As=A's)，于是式(6)第一项为零，很难反映弯矩(或弯扭比)对构件抗扭刚度的影响，但有试验表明［12］，弯矩的存在亦使得构件抗扭刚度降低，弯扭比愈大，退化愈严重。

3 结论

(1)在已有试验的基础上，提出了构件的初始刚度对应的位移角，并给出了抗扭刚度总体退化规律曲线，方便适用，进而可考虑构件开裂后抗扭刚度的降低对结构整体扭转性能的影响。

(2)通过对试验数据及抗扭刚度计算公式的参数分析，探讨了构件抗扭刚度的各种影响因素。纵横钢筋强度比在1附近时构件的抗扭刚度最大，轴压比、偏心距、剪扭比与弯扭比的增大使得构件抗扭刚度降低。

［1］郭长城.建筑结构振动计算［M］.北京:中国建筑工业出版社，1982.GUO Chang-cheng.Building structures vibration［M］.Beijing:China Architecture＆ Building Press，1982.

［2］高层建筑混凝土结构技术规程(JBJ 3－2002)［S］.北京:中国建筑工业出版社，2002.Technical Specification for Concrete Structures of Tall Building(JGJ3－2002)［S］.Beijing:China Architecture＆ Building Press，2002.

［3］沈蒲生，孟焕陵，刘 杨.考虑构件抗扭刚度的高层建筑结构抗扭计算［J］.铁道科学与工程学报，2006，2(3):21－25.SHEN Pu-sheng，MENG Huan-ling，LIU Yang.Calculation of torsion performance of tall building structures based on torsion stiffn［J］.Journal of Railway Science and Engineering，2006，2(3):21 －25.

［4］包世华.新编高层建筑结构.2版［M］.北京:中国水利水电出版社，2005.BAO Shi-hua.New editing tall building structures.Second edition［M］.Beijing:China Water Power Press，2005.

［5］张连德，王泽军，卫云亭.钢筋混凝土偏压扭构件非线性全过程分析［J］.建筑结构学报，1990，11(2):16－27.ZHANG Lian-de，WANG Ze-jun，WEI Yun-ting.Nonlinear full range analysis of reinforced concrete members under eccentric compression and torsion［J］.Journal of Building Structures，1990，11(2):16 －27.

［6］张连德，陈为滢，卫云亭.低周反复扭矩作用下钢筋混凝土双向偏压构件抗扭性能的研究［J］.土木工程学报，1993，26(2):29－373.ZHANG Lian-de，Chen Wei-ying，Wei Yun-ting.Seismic behavior of reinforced concrete members with biaxial eccentric loading under reversed cyclic torsion［J］.China Civil Engineering Journal，1993，26(2):29 －373.

［7］张国顺.钢筋混凝土双向偏压构件抗扭性能的研究［D］.西安:西安建筑科技大学，1989.ZHANG Guo-shun.Torsional strength of reinforced concrete members with biaxial eccentric compression［D］.Xi＇an:Xi＇an University of Architecture ＆ Technology，1989.

［8］赵嘉康，张连德，卫云亭.钢筋混凝土压、弯、剪、扭构件受扭性能的研究［J］.土木工程学报，1993，26(1):20－30.ZHAO Jia-kang，Zhang Lian-de，Wei Yun-ting.Torsional strength of reinforced concrete members subjected to compression，bending，shear and torsion［J］.China Civil Engineering Journal，1993，26(1):20 － 30.

［9］秦卫红.钢筋混凝土压、弯、剪构件在反复扭矩作用下抗扭性能的研究［D］.西安:西安建筑科技大学，1993.QIN Wei-hong.Tentative study on R.C.members subjected to biaxial eccentric compression shear and torsion［D］.Xi＇an:Xi＇an University of Architecture ＆ Technology，1993.

［10］刘继明，时 伟.钢筋混凝土偏压剪扭构件的变形计算方法探讨［J］.工程抗震，2001，23(3):16 －19.LIU Ji-ming，SHI Wei.A study on the method of deformation calculation of reinforced concrete members subjected to eccentric compression with shear and torsion action［J］.Earthquake Resistant Engineering，2001，23(3):16－19.

［11］孙黄胜，施卫星，刘继明.双向偏压剪反复扭构件抗震性能试验研究［J］.同济大学学报，2003，31(10):1151－1156.SUN Huang-sheng，SHI Wei-xing，LIU Ji-ming，Experimental study on aseismic behaviors of RC members subjected to biaxial eccentric compression，shear and reversed torque［J］.Journal of Tongji University，2003，31(10):1151－1156.

［12］王东方，秦卫红.钢筋混凝土压弯剪扭构件的扭转刚度［J］.同济大学学报，2004，32(2):167 －171.WANG Dong-fang，QIN Wei-hong.Torsion stifness of reinforced concrete compression－fIexure－shear－torsion components［J］.Journal of Tongji University，2004，32(2):167－171.

［13］孙黄胜，臧晓光，刘继明.钢筋混凝土复合受扭构件的开裂扭转计算［J］.青岛建筑工程学院学报，2001，22(3):5－8.SUN Huang-sheng，ZANG Xiao-guang，LIU Ji-ming.The calculation of cracking torque of reinforced concrete members subjected to combined torsion［J］.Journal of Qingdao Institute of Architecture and Engineering，2001，22(3):5－8.