基于混合模拟计算法的车辆构架结构可靠性分析
2011-08-07于杨,杨岳
于 杨,杨 岳
(中南大学交通运输工程学院,长沙410075)
车辆构架是车辆走行部的重要构件,其可靠性关系到铁路运输安全,一旦发生故障往往会造成重大行车事故,因此对其结构进行可靠性分析尤为重要。结构可靠度求解方法可分为两类:(1)解析法,由于大部分情况下状态函数与基本随机变量之间的显示函数关系是不存在的,所以解析法的应用受到很大限制。这时一般通过构建响应面,即采用二次多项式函数近似代替状态函数,实现对机械结构可靠性分析的近似计算。(2)数值模拟法,其中以蒙特卡罗法应用最为广泛,但其对大型构件抽样一次的计算量很大,效率很低。而基于建立极限状态方程的响应面法模拟计算则效率高很多,故二者相混合的模拟计算为求解大型构件可靠度提供了一种新方法。本文在ANSYS软件环境下,采用基于蒙特卡罗与响应面相结合的混合模拟计算法进行车辆构架可靠性分析。
1 车辆构架可靠性混合模拟方案
在结构工程有限元分析领域中,ANSYS 软件具有较高的通用性,其可靠性设计系统(PDS)模块为用户进行结构可靠性分析提供了平台。
运用ANSYS进行结构可靠性分析,通常分为3个步骤:生成分析文件,可靠性分析阶段,结果后处理。
1.1 生成分析文件
由3个部分组成。(1)预处理模块:设定单元类型、实常数、材料属性、构建实体模型并进行网格划分。(2)求解模块:定义分析类型及相应选项、施加载荷等并求解。(3)后处理模块:提取计算结果,使用get命令提取计算结果,将值赋给被指定为输入变量、输出结果变量的参数。
1.2 可靠性分析
主要工作包括指定可靠性分析文件、确定各输入变量服从的分布类型和分布函数及各输入变量之间的相关系数、指定输出结果变量、选择分析工具和方法(蒙特卡罗法或响应面法等)、执行可靠性分析循环,将结果以文件形式保存下来。
1.3 结果后处理
通常包括抽样过程显示、绘制设计变量取值分布柱状图和失效概率分布函数、确定输入变量和输出变量的相关系数矩阵、由已知结构的失效概率寻找对应的输入变量、灵敏度分析、生成可靠性分析报告等。
基于混合模拟的可靠性分析与一般可靠性分析过程的区别在可靠性分析阶段,其首先选择蒙特卡罗法进行一次小样本分析,基于蒙特卡罗法的分析结果构建响应面二次多项式进行可靠性分析。基于ANSYS的混合模拟构架可靠性分析流程如图1。

图1 基于ANSYS的混合模拟构架可靠性流程图
2 车辆构架结构强度可靠性分析
2.1 构架结构及材质属性
文中以209系客车车辆转向架构架为例进行可靠性分析,该系列构架形式为铸钢一体H形,结构具有左右对称性;同时针对一种载荷工况(垂直总载荷)进行有限元可靠性分析,因此其还具有前后对称性,故可仅对其四分之一模型进行分析。材质为ZG25,其弹性模量ex=1.75×105MPa,服从正态分布,变异系数为0.03;泊松比prxy=0.3,服从正态分布,变异系数为0.03;密度为7.8 t/m3,正态分布,变异系数为0.01。
2.2 模型的建立
由于构架模型较为复杂,ANSYS三维建模功能不足,故在三维软件SOLIDWORKS中建立构架三维模型,如图2。通过格式*.x-t转换输入到ANSYS中。

图2 构架三维CAD模型
2.3 载荷工况及材料特性的确定
根据文献[7] ,构架试验载荷分为3种:垂直总载荷,侧向力载荷,斜对称载荷。一般情况下,其侧向力载荷、斜对称载荷相对垂直总载荷小得多,故优先选取垂直总载荷工况进行可靠性分析。
假设垂直总载荷服从对数正态分布,其均值为65 kN,变异系数为0.05。根据文献[7] 中规定,材质ZG25的许用应力均值为135 MPa。材料强度极限服从对数正态分布,变异系数为0.06。各随机变量输入数据如表1。
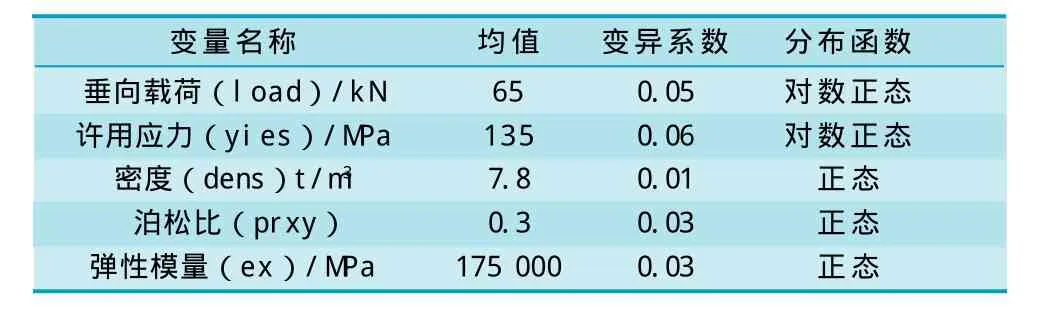
表1 随机变量输入数据
2.4 在ANSYS中进行可靠性混合模拟分析
在ANSYS软件Solution模块中完成构架有限元分析后,应用General Postproc模块将节点等效应力排序。
在命令窗口输入APDL文件语句*get,maxstr,sort,max,获得最大的节点等效应力;maxstr代表最大的节点等效应力。
定义极限状态方程,yies代表构架许用应力,Z代表许用应力与最大应力之差,说明构架是可靠的,说明构架将会失效。进行构架可靠性分析,其实质就是求解目标变量Z值大于零的概率。
生成概率分析APDL文件*.pdan。进入ANSYS软件概率分析模块(PDS),进行构架可靠性分析。指定概率分析文件为*.pdan。定义随机变量垂向载荷、许用应力、密度、泊松比、弹性模量等(如表1);定义输出目标变量Z;选择蒙特卡罗法,采用超拉丁抽样,仿真300次,循环1次,设置执行标签为MCRUN,进行可靠性分析。进入响应面模拟,拟合响应面方程,设置标签为RSMRUN,选择求解标签MCRUN,输出参数Z,置信度为95%;进入响应面法仿真,仿真10 000次。
3 构架结构可靠性结果分析
3.1 可靠度计算及耗时分析
(1)蒙特卡罗法采用拉丁超立方抽样,模拟300次,重复1个循环。
在置信度为95%时,目标变量Z值小于0的概率F(z<0)为0.075%,其可靠度R(z>0)为99.925%。
(2)在蒙特卡罗法分析基础上,拟合响应面状态函数,计算构架可靠度。
响应面法模拟10 000次,在置信度为95%时,Z值小于0的概率F(z<0)为0.053%,则可靠度R(z>0)为99.947%。
(3)计算耗时分析
本次模拟计算平台为奔腾Ⅳ 2.67 G,768 M内存的计算机,达到抽样300次蒙特卡罗法需要耗时2.5 h;达到同样抽样10 000次,蒙特卡罗抽样可靠度计算共耗时83.3 h,而基于响应面的混合模拟抽样可靠度计算共耗时3 h,后者在计算效率上具有明显的优势。
3.2 Z均值趋势图
Z均值趋势图如图3。可以看出随着模拟次数的增加,曲线逐渐趋于平直,说明只要仿真次数足够多,可靠度值会逐渐趋于一个稳定值。150次模拟后,Z值均值趋势已近于平直,表明此后的可靠性分析结果具有可信度。同时表明,蒙特卡罗仿真300次抽样试验点及响应值具有代表性,其拟合的响应面函数可近似替代极限状态曲面。
3.3 Z值柱状图
图4、图5分别为基于蒙特卡罗法和基于混合模拟法的Z值柱状图。柱状图用于描述目标变量Z值的分布,将目标变量Z取值范围等间距均分,根据属于各间距的抽样点个数可确定柱状图形状。由于5个输入变量均为正态分布,可推断目标变量Z值亦为正态分布。
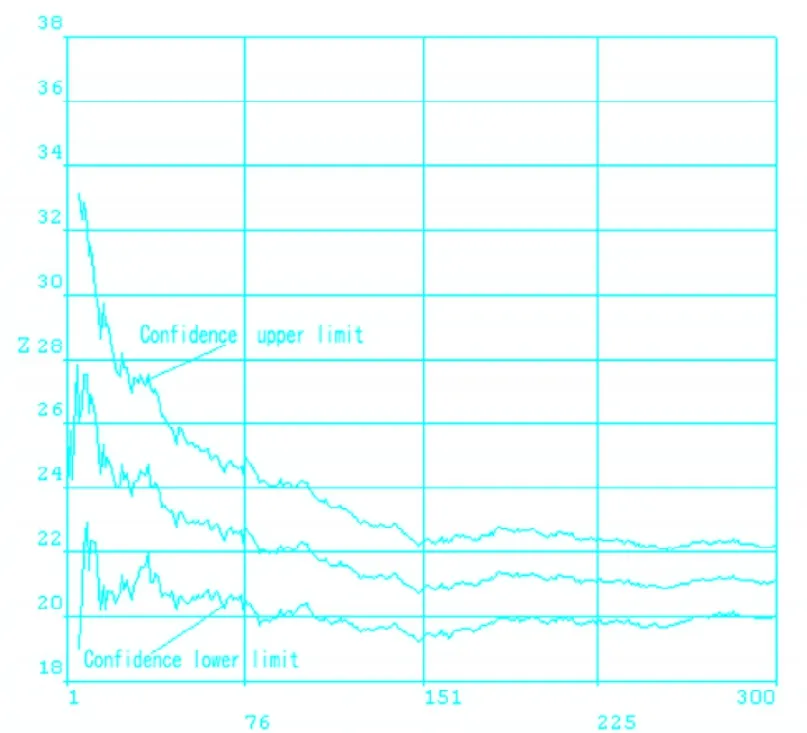
图3 蒙特卡罗法目标变量Z的均值样本走势图

图4 基于蒙特卡罗法的目标变量Z值柱状图
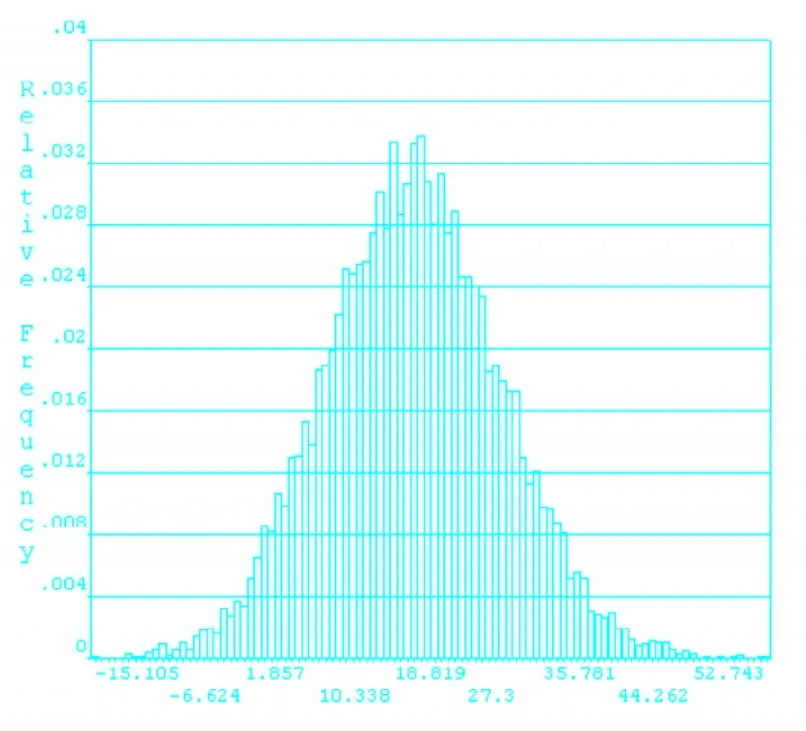
图5 基于混合模拟法的目标变量Z值柱状图
由图4和图5可以看出,当输入变量为正态分布、对数正态分布时,其输出目标变量分布亦趋近为正态分布,与理论分析吻合,表明可靠性分析过程是合理的。目标变量Z值柱状图拟合近似分布函数曲线,说明模拟次数足够。混合模拟次数较多,故其更接近正态函数分布曲线。
3.4 灵敏度分析
图6、图7分别为基于蒙特卡罗法和基于混合模拟法的目标变量Z值灵敏度分析图。对目标变量Z值进行灵敏度分析,通过判断输入随机变量在柱状图中的长度和在饼状图中所占比例得出随机变量对可靠度影响的程度,即可分清哪些因素是影响可靠性的重要因素,哪些是次要因素。

图6 基于蒙特卡罗法的灵敏度分析

图7 基于混合模拟法的灵敏度分析
通过对比图6、图7可以看出,蒙特卡罗的灵敏度分析仅能得到许用应力与载荷等两个输入变量对构架可靠性的影响;混合模拟法的灵敏度分析可以得到许用应力、载荷和泊松比等3个输入变量对构架可靠性的影响。由此可见,混合模拟法灵敏度更高,分析结果更精确。
由图7可以看出,影响构架可靠性的主要因素是许用应力,其次为载荷,再次为泊松比。
4 结束语
论文基于蒙特卡罗统计抽样,形成实验设计数据,拟合极限状态方程进行可靠性分析的思想。在ANSYS有限元分析软件支撑下,采用基于蒙特卡罗与响应面混合模拟法,对209系车辆构架可靠性进行了分析计算,显示了该方法在可靠性分析中的高效性,可为大型构件的可靠性分析提供参考。
[1] 戚松,赵洪伦,王社峰. 运用ANSYS软件与蒙特卡罗法相结合的随机有限元方法进行车辆构件强度可靠性分析[J] . 铁道车辆,2009,47(2):6-9.
[2] StefanReh,Jean-DanielBeley,SiddharthaMukherjee,EngHui-Khor.Probabilistic finite element analysis using ANSYS[J] .Structural Safety, 2006(28):17-64.
[3] 张伟.结构可靠性理论与应用[M] .北京:科学出版社,2008.
[4] 余伟炜,高炳军. ANSYS在机械与化工装备中的应用[M] .北京:中国水利水电出版社,2006.
[5] 顾典康. 209系列转向架构架强度试验分析[J] . 铁道机车车辆,2004(4):11-12.
[6] 张建国,苏多,刘英卫. 机械产品可靠性分析与优化[M] .北京:电子工业出版社,2008.
[7] 铁道车辆强度设计及试验鉴定规范[S] . 北京:中华人民共和国铁道部,1996.
