对称圆弧加直线修正型线涡旋压缩机脱啮角与排气角研究
2011-08-03刘向农王铁军刘正士
吴 昊 刘向农 王铁军 刘正士
(合肥工业大学机械与汽车工程学院 合肥 230009)
用于传统汽车空调的开启式涡旋压缩机和电动汽车空调的封闭涡旋压缩机采用对称圆弧加直线(EA-SAL)对涡盘始端进行修正[1-3],增大了排气角,提高了压缩机的内容积比和压缩比,改善了涡盘始端切削受力特性,以满足汽车空调工况、工质要求和安装空间限制的特殊要求。对称圆弧加直线修正型线涡旋压缩机的排气过程,特别是排气角的确定,在涡旋压缩机的修正设计计算中尤为重要。国外汽车空调压缩机主要生产厂家日本三电和电装公司都生产这种齿形的涡旋压缩机,但相关研究成果迄今为止未见有公开发表。国内学者对修正型线涡旋压缩机的排气过程及排气角也有一定研究。刘涛等分析了双圆弧修正时的开始排气角[4]。高秀峰等简单地分析了设有排气阀的涡旋压缩机排气角的确定,并指出涡盘始端修正后容积的计算公式比较复杂[5];在计算压缩机工作容积时,将排气过程分为渐开线啮合阶段和修正部分啮合阶段[6]。靳林芳等通过研究修正型线压缩机的排气过程,提出了排气孔设计应遵循的原则,同时指出要更正现行的热力、动力计算中排气角的大小[7]。在有关对称圆弧加直线修正的文献中,将排气角等同于动静涡盘相互脱啮时主轴转过的角度,这未能真实反映排气状况,导致在计算各压缩腔容积时产生较大误差;尤其没有涉及中心压缩腔容积计算方法,而这关系到涡旋压缩机动力分析与计算。这里就对称圆弧加直线修正型线涡旋压缩机涡盘始端的几何特性作了深入分析,严格区分形成中心压缩腔时主轴转过的角度和压缩机排气时主轴转过的角度,定义了脱啮角和实际排气角,详细推导了脱啮角计算公式,分析了影响脱啮角大小的因素。针对修正后中心压缩腔容积减少实际上是由于涡盘始端壁厚增加造成的本质特点,提出了修正后涡盘始端壁厚增加的容积的计算方法,从而计算出中心压缩腔容积和实际排气角大小。这些对准确计算各压缩腔容积尤其是中心压缩腔容积、动力分析与设计计算都十分重要。
1 对称圆弧加直线修正参数
如图1所示,涡盘本体采用渐开线型线,基本几何参数为:基圆半径为rb,涡盘节距为P,涡盘壁厚为t,渐开线起始角为α,φ为渐开角。涡盘始端采用对称圆弧加直线修正,修正角为β,A点为修正圆弧与涡盘内壁渐开线交点,点为连接圆弧与涡盘外壁渐开线交点,为修正直线,与修正圆弧和连接圆弧分别相切于、N点。连接圆弧半径为r,修正圆弧半径为,修正圆弧中心O2' 与基圆切点C距离为d。

图1 对称圆弧加直线修正涡盘Fig.1 Scroll with symmetrical circular arc plus line-shaped top pro fi le
2 脱啮角
2.1 主轴转角
将动涡盘相对静涡盘180°安装时主轴转角定义为θ=0,即静动涡盘基圆圆心连线OO'与X轴正向夹角为0,那么,动涡盘在作平动时其基圆圆心O'绕静涡盘基圆圆心O转过的角度为主轴转角θ,如图2所示。
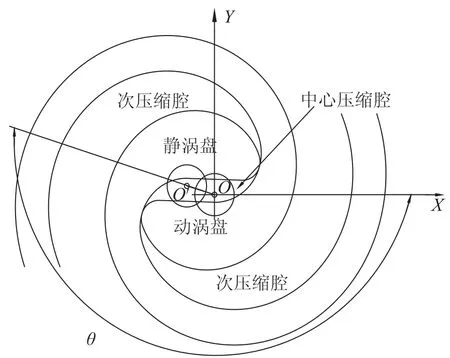
图2 主轴转角Fig.2 Rotating angle of crankshaft
2.2 脱啮角
在圆弧加直线修正方法中,一般将次压缩腔与中心腔连通时,主轴转角定义为排气角。实际上,由于压缩终了内容积比较小,内压力比也较小,还未达到外压力比(汽车空调工况下,外压力比接近6,而通过计算发现,内压力比仅仅3~4之间),显然,尽管次压缩腔与中心腔已经连通,但还不能将制冷剂气体排出,如果将此时主轴转角定义为排气角,则不能反映涡旋压缩机内部真实的排气状况,因此这种定义不尽合理。也有文献提出将次压缩腔与中心压缩腔连通时主轴转角定义为脱啮角[7],并且规定涡旋体最外侧封闭时主轴转角θ=0,这不便于计算各压缩腔容积[8-9]。这里将中心压缩腔与次压缩腔连通瞬间动涡盘和静涡盘齿端直线部分相互脱啮时,动涡盘相对静涡盘转过的角度(即主轴转过的角度)定义为脱啮角,记为θ*,并且规定动涡盘相对静涡盘180°安装时主轴转角定义为θ=0,即静动涡盘基圆圆心连线OO'与X轴正向夹角为0,如图3所示。
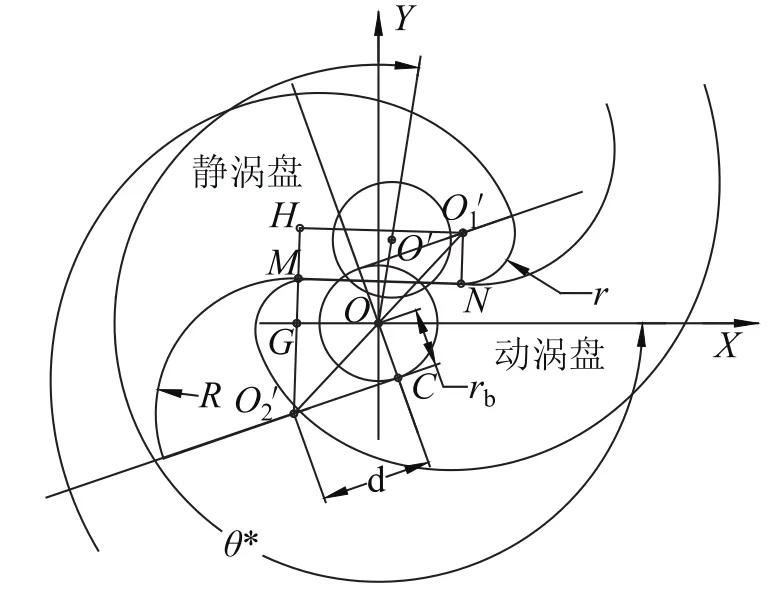
图3 脱啮角Fig.3 Mesh-apart angle
那么,从初始位置动涡盘基圆中心O'位于过静涡盘基圆中心O的水平线上,且(回转半径),转到此位置时,

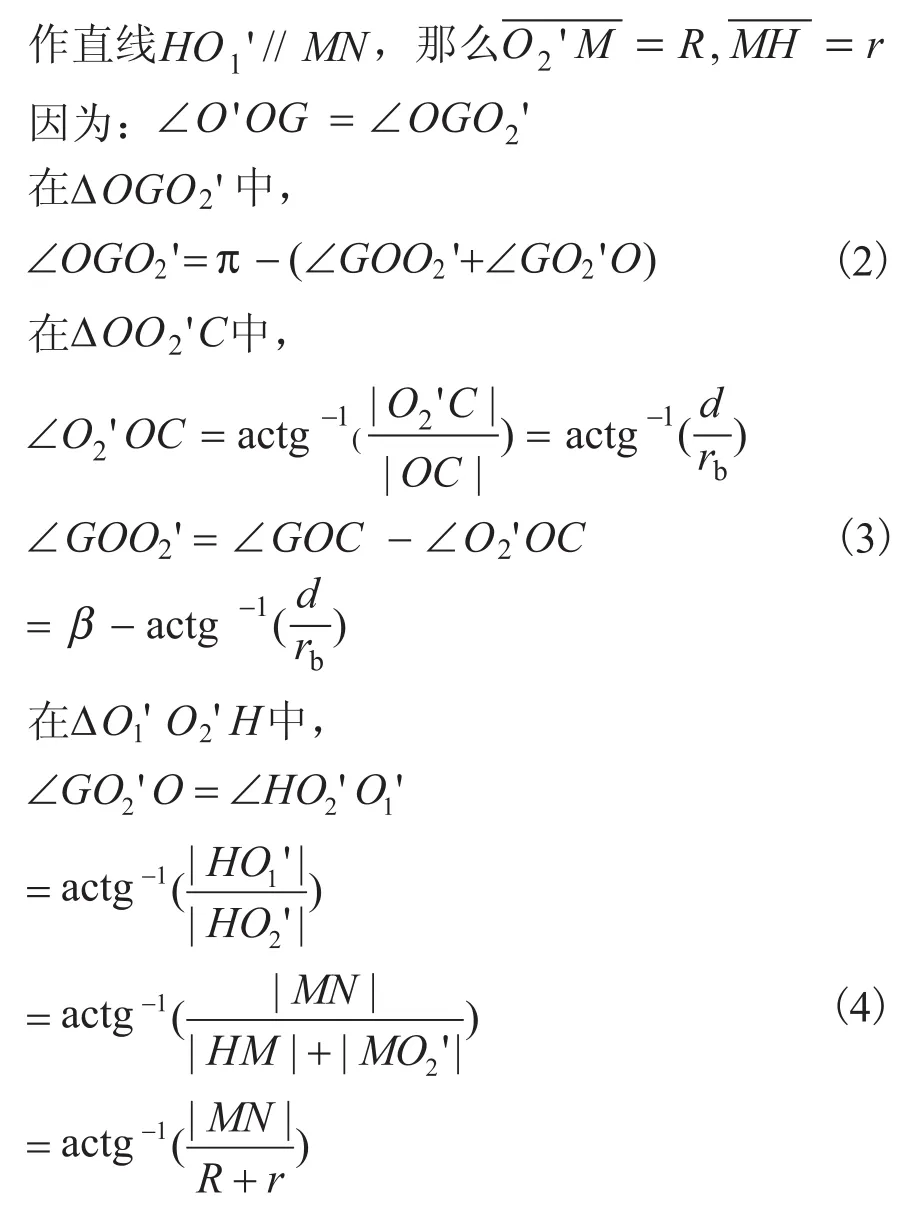
将公式(2)、(3)、(4)代入公式(1)中,得到:
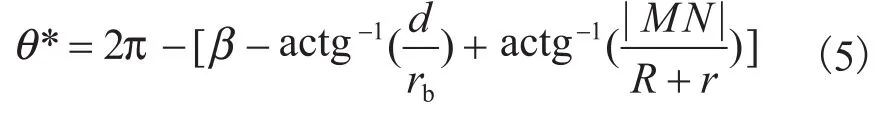
2.3 影响脱啮角大小的因素
如图1所示,rc与Rc分别是双圆弧修正时连接圆弧与修正圆弧半径,圆心分别为O1与O2,修正圆弧中心O2与基圆切点C距离为dc。对称圆弧加直线修正时,将O1与O2分别沿其所在的基圆展开线移动Δr1与Δr2(对称圆弧加直线修正时偏移量Δr=Δr1=Δr2)至O1'与O2',各参数有如下关系[7]:
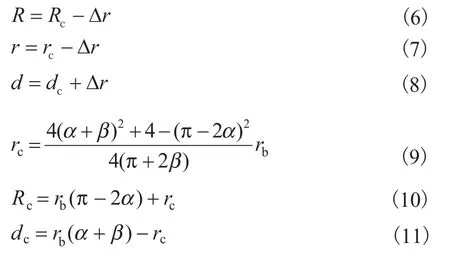
可以看出:r、R、d与渐开线涡旋体基本几何参数、修正角β及偏移量∆r有关。
直线 的长度为[6]:

因此,当渐开线涡旋体几何参数确定时,由公式(5)得到:脱啮角θ*与修正角β及偏移量∆r相关,随后者变化关系如图4所示。
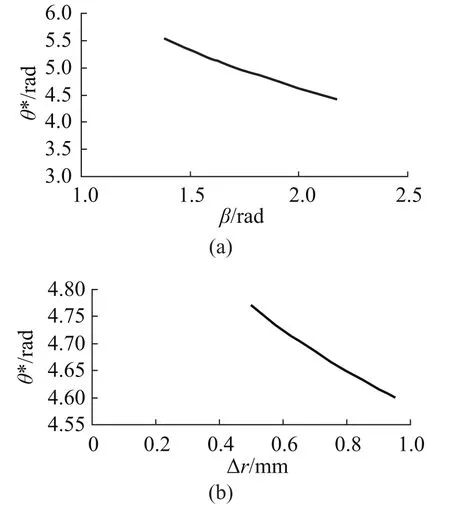
图4 脱啮角θ*与修正角β及偏移量Δr变化关系示意图Fig.4 The relationship between mesh-apart angle θ* and modi fi catory angle β and offset Δr
3 实际排气角
中心压缩腔与次压缩腔连通后,由于压力没达到排气压力,制冷剂气体在中心压缩腔中继续被压缩直到达到排气压力,此时主轴转过的转角定义为实际排气角,记为θd(图5)。
3.1 中心压缩腔容积
经对称圆弧加直线修正后,涡旋压缩机的中心压缩腔容积计算比较繁琐,至今未见有文献作相关阐明。高秀峰等给出了排气过程的修正部分啮合阶段封闭工作腔容积计算方法[6],但实际排气开始时,中心压缩腔投影面积S如图6所示,此时修正部分未能相互啮合。因此,公式不能适用于实际排气时中心腔容积计算。鉴于未修正时中心压缩腔容积由渐开线涡旋壁和动静涡盘端面所形成,且易于计算[10],如果修正后涡盘始端相比较未修正时壁厚增加的容积能计算出来,那么中心压缩腔的容积也容易计算了。
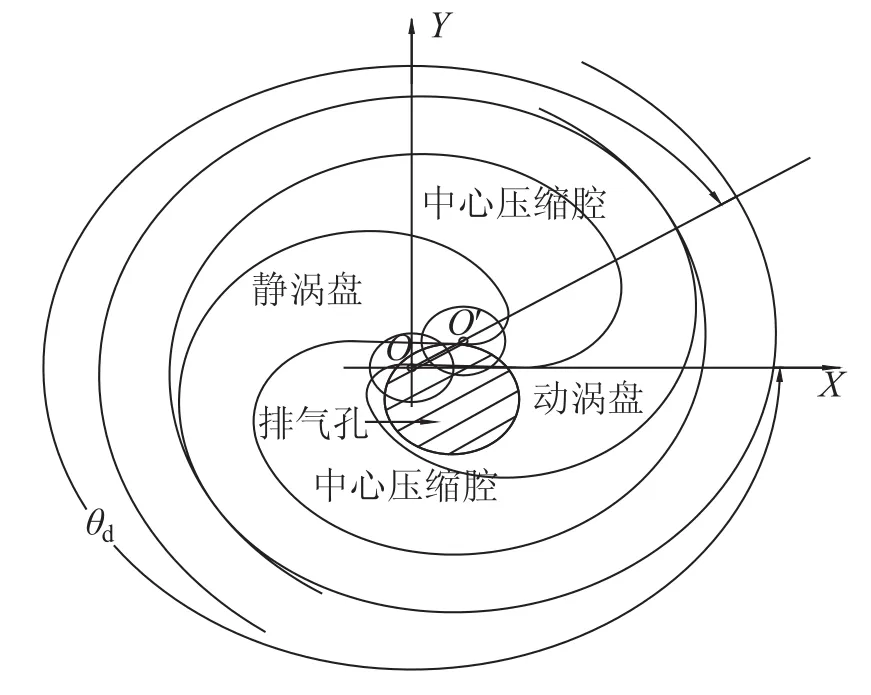
图5 实际排气角Fig.5 Actual discharge angle
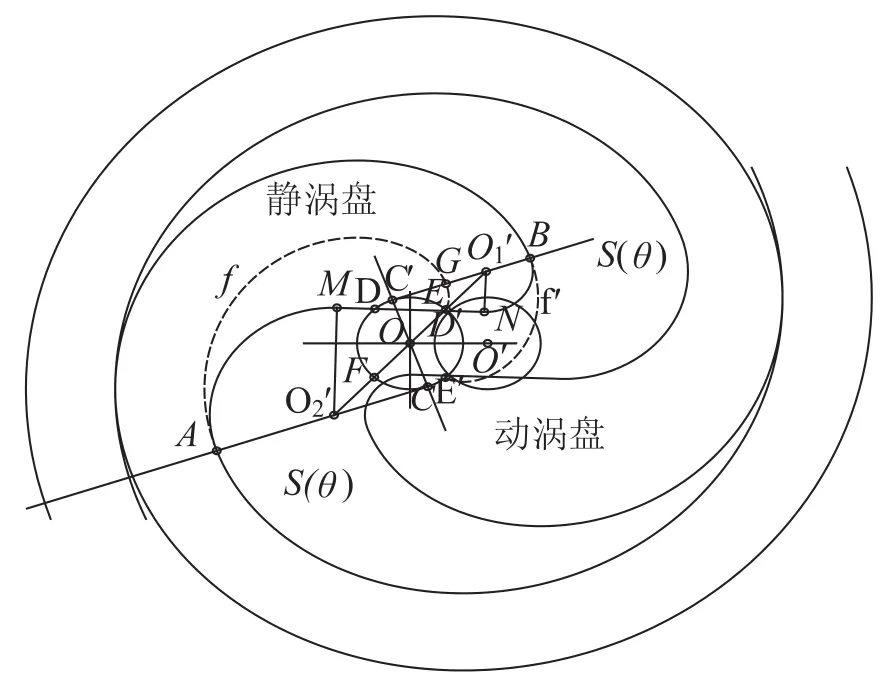
图6 实际排气中心压缩腔Fig.6 Actual centre compression chamber of discharge
1)修正后始端壁厚增加的容积
通过对中心压缩腔的几何特性深入研究后发现,修正后涡盘始端由于壁厚增加导致其投影面积增加,增加部分可以用S'(θ)表示:
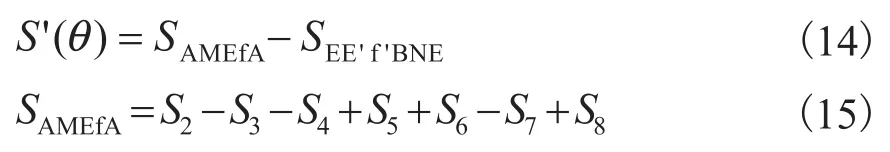
式中:S2~S8—渐开线内壁从起始点E到A点包围面积,扇形O2'MA面积,三角形O2'MD'面积,扇形ODF面积,三角形DOD'面积,三角形OCO2'面积,扇形OFC面积。
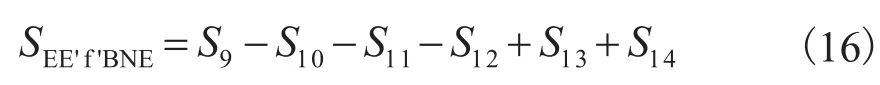
式中:S9~S14—渐开线外壁从起始点E´到B点包围的面积,扇形O1'NB面积,三角形O1'ND′面积,三角形OC'O1'面积,扇形OC'D'面积,渐开线内壁从起始点E到G包围的面积。
修正后由于壁厚增加而增大的容积:

这部分增加的容积直接导致中心压缩腔容积减少。
2)中心压缩腔容积
相对于未修正时中心压缩腔投影面积S1[9],经对称圆弧加直线修正后,中心压缩腔投影面积S可以用下式计算:


3.2 实际排气角计算
实际排气角的计算,可以利用外压比反推得到。根据汽车空调工况,易知压缩机排气压力Pd,吸气压力Ps。那么,涡旋压缩机吸气容积


式中:k—制冷剂气体的压缩指数。
因此,由(19)、(20)、(21)式得到:

令θ=θd,代入(22)式中,通过数值解法可以求解θd。
3.3 运算实例
已知涡盘参数:节距15.7mm,壁厚4.2mm,高度14mm,三对压缩腔,对称圆弧加直线修正,修正角为1.908rad,汽车空调工况下,制冷剂R134a,排气压力1804kPa,吸气压力293kPa,计算结果为:内容积比ν1=2.744,内压力比ε1=3.035,脱啮角θ*=4.744rad,实际排气角θd=6.368rad。
即主轴转过272°时动静涡盘修正直线部分相互脱啮,次压缩腔与中心压缩腔连通;当主轴转过365°时,中心压缩腔里制冷剂气体压力才达到外压比(ε=6.16),开始排气。显然,脱啮角和实际排气角有相当大的区别。
4 结论
1) EA-SAL修正涡旋齿方法中,脱啮角是计算各压缩腔容积的关键参数,这里定义了脱啮角并详细推导了脱啮角的计算公式,分析了影响脱啮角大小的因素。
2) 提出了经EA-SAL修正后涡盘始端壁厚增加的容积的计算方法,为中心压缩腔容积的计算及动力分析计算提供了依据。
3) 准确定义了实际排气角,利用外压比反推出实际排气角。通过运算实例对比了脱啮角与实际排气角相差很大。
4) 由于实际排气过程的推迟,中心压缩腔容积继续变小,不仅增大了内容积比,还将影响两相邻压缩腔由于压差变化所产生的泄漏、动静涡盘脱啮后中心压缩腔实际存在的减容压缩过程中的传热特性、排气开始和结束阶段工质的流动阻力和功损耗,这些因素影响到排气孔口的设计,相关内容有待于进一步探讨。
[1]Lee Yinren, Wu Wenfang. On the pro fi le design of a scroll compressor[J]. International Journal of Refrigeration,1995,18 (5) : 308-317.
[2]高秀峰,郁永章. 涡旋齿端圆弧类型线修正概述[J].流体机械, 2001, 29(12):25-29.(Gao Xiufeng, Yu Yongzhang. Summary on Modi fi cation of Top Pro fi le with Arc-Shaped Curves for Scroll[J]. Fluid Machinery, 2001,29(12): 25-29.)
[3]高秀峰. 圆弧类涡旋修正齿型的设计方法研究[J]. 流体机械, 2005, 3(1): 11-14.(Gao Xiufeng. Study on Design Method of Top Wrap Modified by Arc-Shaped Curves for Scroll Machinery[J]. Fluid Machinery, 2005, 3(1):11-14.)
[4]刘涛,刘振全,邬再新. 修正型线涡旋压缩机的内容积比确定方法[J].流体机械, 2003, 31(10): 12-14.(Liu Tao, Liu Zhenquan, Wu Zaixin. Determination Method on Volume-reduction Ratio for Scroll Compressor with Modified Profile[J]. Fluid Machinery, 2003, 31(10):12-14.)
[5]高秀峰, 郁永章. 对称修正齿端涡旋压缩机排气孔研究[J]. 压缩机技术, 1999, 5: 3-7. (Gao Xiufeng,Yu Yongzhang. Study on Discharge Port for Scroll Compressor with Symmetric Shaped Top Wrap[J].Technique of Compressor, 1999, 5: 3-7.)
[6]高秀峰, 刘卫华, 冯诗愚, 等. 涡旋齿端等β角圆弧类型线修正理论的研究[J]. 西安交通大学学报, 2001,35(7):750-754.(Gao Xiufeng, Liu Weihua, Feng Shiyu,et al. Theoretical Study on Modification of Top Profile Based on Arc-Shaped Curves with Equal Beta Angle for Scroll Fluid Machinery[J]. Journal of Xi'an Jiaotong University, 2001, 35(7):750-754.)
[7]靳林芳, 熊则男. 涡旋压缩机的涡旋型线始端修正及排气过程研究[J].压缩机技术, 1999, 2:3-6.(Jin Linfang,Xiong Zenan. Study on Modification of Top Profile and Discharge Process for Scroll Compressor[J]. Technique of Compressor, 1999, 2:3-6.)
[8]郁永章. 容积式压缩机技术手册[M]. 北京: 机械工业出版社, 2000: 728-772.
[9]缪道平, 吴业正. 制冷压缩机[M]. 北京: 机械工业出版社, 2003:139-142.
[10]B Blunier, G Cirrincione, Y Herve, et al. A new analytical and dynamical model of a scroll compressor with experimental validation[J]. International Journal of Refrigeration, 2009, 32: 874-891.
[11]强建国, 刘振全. 修正涡旋齿端面积计算[J]. 兰州理工大学学报, 2006, 32(5): 36-39.(Qiang Jianguo, Liu Zhenquan. End cross-section area calculation of EA-SAL modi fi ed scroll wrap[J]. Journal of Lanzhou University of Technology, 2006, 32(5): 36-39.)
