一种改进的球形解码算法

王 宁，李 君，金 宁

（中国计量学院 信息工程学院，浙江 杭州 310018）

近年来，随着因特网和多媒体应用在下一代无线通信中的集成，宽带高速数据通信服务的需要正在不断增长.另一方面，可利用的无线频谱是有限的，如果通信频谱的利用率没有得到显著提高，就不能满足通信容量的需求.信息论的研究证明，在发送端和接收端都采用多天线的MIMO技术可以大量提高频谱利用率，这使其在通信领域得到了广泛的应用［1］.信号的检测性能对MIMO系统的性能至关重要，因此，MIMO系统中的检测算法是当前研究的重点.

在MIMO信号检测算法中，最大似然（ML）检测是在误比特率最小的意义下的最优接收，但其计算复杂度随着发射天线数及调制星座点数的增加而呈指数增长，这使其成为一个NP问题.除此之外，还有一些次优的检测算法，如迫零（ZF）算法、最小均方误差（MMSE）算法、串行干扰抵消（V－BLAST）算法等，这些算法的复杂度较低，但其误比特率性能较差.

近年来出现了一些准最大似然检测算法，球形解码算法就是其中之一.球形解码算法通过设定一个以接受向量为中心的超球，仅搜索超球内的格点来找到最大似然解，从而避免了繁琐复杂的搜索，降低了球形解码算法的复杂度，使其在很大的信噪比范围内与天线数呈多项式关系［2］.

但在低信噪比范围内或调制阶数较高时，球形解码算法的复杂度仍然是很高的，这也是近年来球形解码算法研究的重点.信号的检测顺序与球形解码算法的复杂度密切相关，因此可以通过对信道矩阵的列进行重排来改变信号的检测顺序［3-13］，从而减低球形解码算法的复杂度.文献［3］以信道矩阵的列范数作为依据；文献［4，5］则将最优检测顺序的V－BLAST［6］算法运用到球形解码中；文献［7－10］是基于排序的QR分解算法，将排序算法嵌入在QR分解的过程中，其中文献［7］只考虑了信道矩阵，文献［8－10］则综合考虑了信道矩阵和接收向量；文献［11－13］中提出用迫零算法的初始估计值作为参考来确定发射向量的可靠性，从最可靠的元素开始检测.这些改进算法都不同程度地降低了球形解码算法的计算复杂度，但在高信噪比范围内，由于球形解码算法中SE搜索策略的限制，其复杂度最终会收敛于2m－1.本文所提出的算法主要针对高信噪比范围内球形解码算法复杂度的进一步降低，通过累积分布函数得到一个阈值，在搜索到叶子节点后，将其累积度量值和阈值进行比较来判断是否找到最大似然解，从而降低了球形解码算法在高信噪比范围内的复杂度.

1 系统模型

考虑一个未编码的MIMO系统，发射天线数为M，接收天线数为N（N≥M），假定信道是平坦瑞利衰落的，其接收信号可表示为：

上式中采用复数信号模型，其中y＝［y1，y2，...，yN］T是N×1的接收信号向量.s＝［s1，s2，...，sM］T是M×1的发射信号向量.H 是N×M的信道矩阵，H的每一个元素hi，j都是独立同分布的复高斯随机变量，且其均值为零，方差为1.w为加性高斯白噪声，服从复高斯分布，且其均值为零，方差为σ2.

为了简化编程细节，我们通常先将信号模型从复数域转换到实数域，转换后各个量的维数加倍，即m＝2 M，n＝2 N.

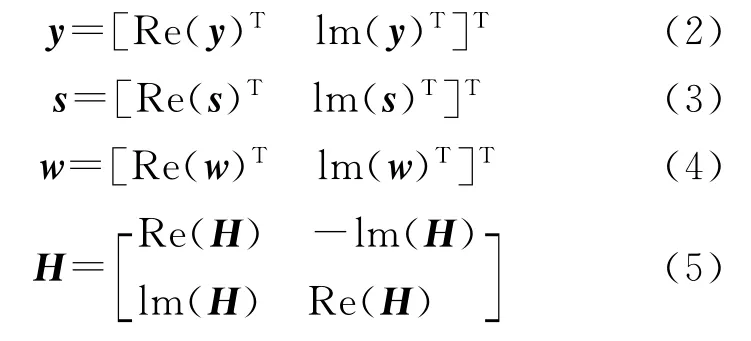
假设发送符号采用L2－QAM调制方式（QAM是指正交幅度调制），则s的每个元素有L个可能取值，在信道已知的条件下，接收端的最大似然检测可表示为：

其中下标中的集合D代表所有可能的发送信号向量的集合，‖·‖代表向量的欧氏范数.

球形解码的基本思想是在一个以接受向量为球心的超球内搜索格点，离球心最近的格点即为相应的译码.通过仅搜索超球内部的点，而避免了搜索整个格点集合，其具体算法如下：

假定球形解码的初始半径为d0，则在超球内的点必须满足：

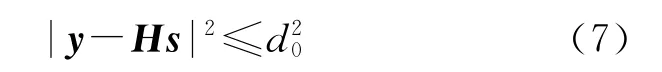
对H进行QR分解，可得：

其中，R是m×m的上三角矩阵，（·）＊表示矩阵的Hermitian转置.Q＝是n×n的酉矩阵，Q1和Q2分别代表矩阵Q的前m列和后n－m列.在此，令d2＝－，z＝y，则式（8）可变为：

利用上三角矩阵R可将上式右边展开，可得：

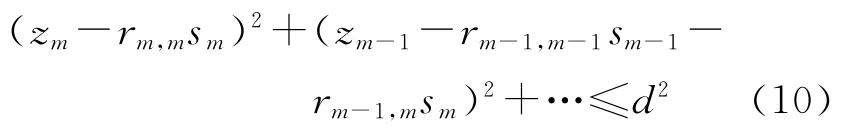
通过上式我们可以得到sm的取值范围，之后通过迭代可依次得到sm－1、sm－2直至s1的取值范围，从而形成一个深度为m的树形搜索结构，如图1所示.当搜索到叶子节点即树的最底层时，若其累积度量值小于当前半径，则可将半径更新，继续搜索，直至找到累积度量值最小的格点，即最大似然解.

图1 球形解码算法的树形搜索结构示意图Figure 1 Search tree of the sphere detection algorithm

在球形解码算法的树形搜索过程中，有两种搜索策略，分别是 Fincke－Pohst（FP）策略和Schnorr－Euchner（SE）策略.这两种策略的主要区别是在枚举候选节点时的顺序，FP策略在访问下一层节点时按照信号星座的顺序，从左到右依次枚举信号星座点.SE策略则是将下一层的信号星座点按其当前层的度量值从小到大排序，在访问下一层节点时按此顺序枚举.

SE策略是以折线搜索（zig－zag）的方法进行，该算法搜索的第一个点为当前层度量值最小的点，因此若搜索失败，则可直接跳过该层剩余节点，从而大大减少了算法的计算复杂度.

SE策略在半径设为无穷时搜索到的第一个点即为Babai点，因此SE策略对半径的选择不敏感.由于SE策略是从最小化分支度量的节点开始搜索，所以能比FP策略更快的找到最大似然解，其复杂度也相对更低，因此对球形解码算法的研究也主要是基于SE策略.

2 改进的球形解码算法

球形解码算法中，对信道矩阵H进行QR分解所得到的上三角矩阵R决定了信号的检测顺序，但这个顺序并不一定是最优的求解顺序.因此，可以通过对信道矩阵H的列进行重排来改变信号的检测顺序，降低球形解码算法的复杂度.在文献［3－13］中，研究人员提出了许多种不同的排序策略来对信道矩阵的列进行重排，从而改变信号的检测顺序，这些改进算法均不同程度的降低了球形解码算法的复杂度，特别是在低信噪比范围内，但在高信噪比范围内，由于SE搜索策略的限制，各算法的展开节点数均收敛于2m－1，本文所提出的算法主要针对高信噪范围内球形解码算法复杂度的降低.

采用SE策略，在初始半径为无穷时搜到的第一个点为Babai点，而在高信噪比范围内，这个点有很大的概率即为最大似然解.但由于SE策略的限制，此时并不能立即判决该点是否为最大似然解，而只有继续回溯直到第一层，若此时仍是Babai点的累积度量值最小则表明找到最大似然解.因此，我们可以设法找到一个阈值，在搜索到叶子节点后将其累积度量值和阈值比较，若其小于阈值，我们可认为最大似然解已经找到，停止搜索，而不必继续回溯，从而降低球形解码算法的复杂度.

对于实际的传输向量，总的累积度量值可以表示如下：

其中qi代表矩阵的第i列，上式中ωi～N（0，σ2），所以‖ωi‖2服从自由度为1的χ2分布，而Q1为酉矩阵，并不会改变‖ωi‖2的分布，因此累积度量值P服从自由度为m的χ2分布，并且正确格点的累积度量值服从中心的χ2分布，而错误格点的累积度量值则服从非中心的χ2分布，如图2所示.

从图2中可以看出，若某个格点的累积度量值在正确格点和错误格点交点的左侧，则该点是正确格点的概率要大于其是错误格点的概率，而越往左侧，该点是正确格点的可能性就越大.因此，我们可以选定一个概率值ε，根据正确格点的累积分布函数得到一个阈值，作为判断最大似然解的依据.若搜索到某个叶子节点后，其累积度量值小于阈值，我们认为最大似然解已找到，停止搜索，否则继续搜索.

ε的取值对球形解码算法的性能也有一定的影响，若ε取值过大，即表明阈值过大，此时，误码率也相应较高，特别是在低信噪比范围内.而在高信噪比范围内，若ε取值过小，即阈值过小，则会降低阈值对球形解码算法的约束作用，以致对高信噪比范围内球形解码算法的复杂度影响不大.基于上述原因，我们在选取阈值时应对球形解码算法的性能和复杂度作一个权衡，在低信噪比范围内减小阈值，而在高信噪比范围内则适当加大阈值.

图2 χ2分布的概率分布图Figure 2 Probability distribution of theχ2 distribution

3 仿真结果分析

在仿真过程中，将本文所提到的阈值运用到了不同排序策略的球形解码算法中，这其中包括文献［3］中的 V－BLAST算法，文献［12］中的梯度（GRA）算法以及文献［10］中的均衡排序的QR分解（BSQR）算法.本文对各算法的性能和复杂度均做了比较，采用树形搜索结构中展开的节点数作为复杂度的判断依据.

图3为4×4及6×6的MIMO系统中采用16QAM、64QAM星座调制方式下各算法的误符号率性能图.当信噪比为0～19dB时，ε＝0.05，当信噪比为20～30dB时，ε＝0.4.从图中可以看出，由于在低信噪比范围内阈值较小，此时采用阈值后和原来的球形解码算法相比性能相差不大；而在高信噪比范围内阈值较大，此时采用阈值后相比原来的球形解码算法性能要差些，若想提高其性能，可通过减小阈值来实现.

图3 不同算法的误符号率性能图Figure 3 SER performance of different algorithms

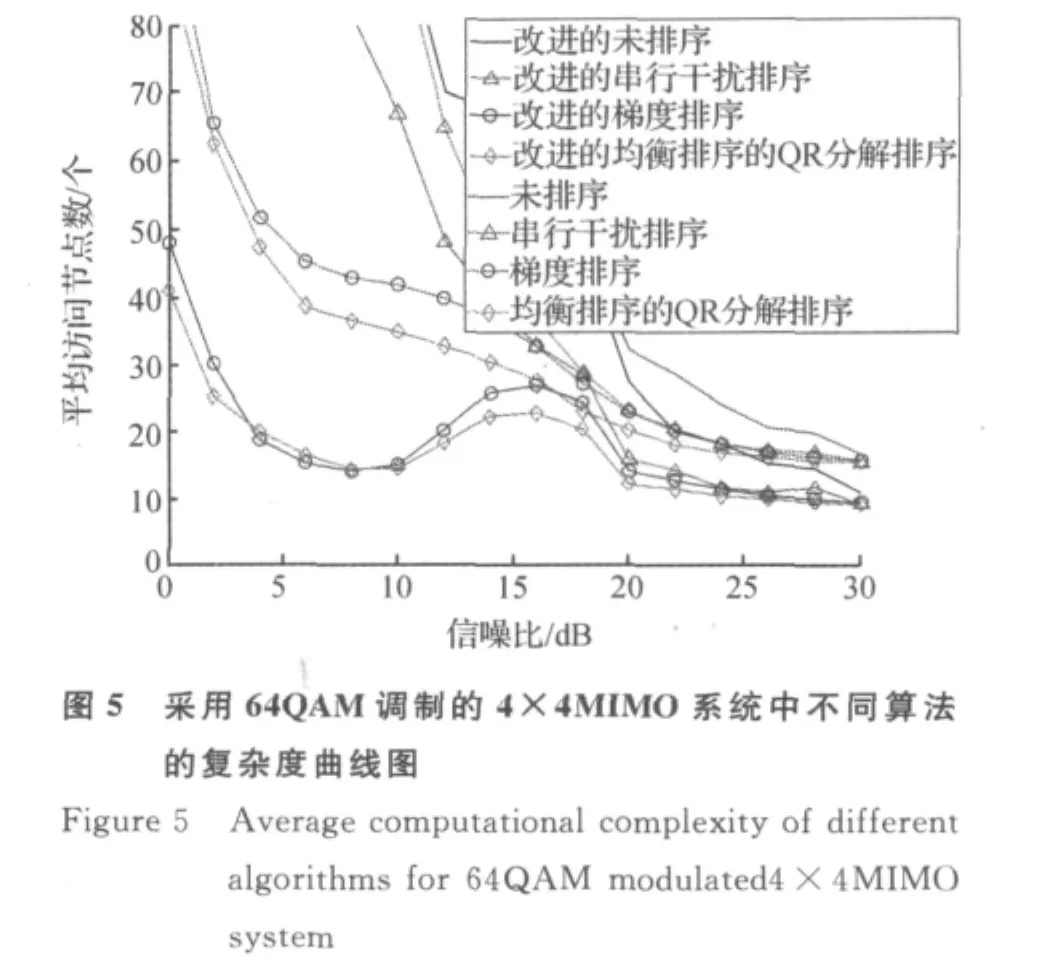
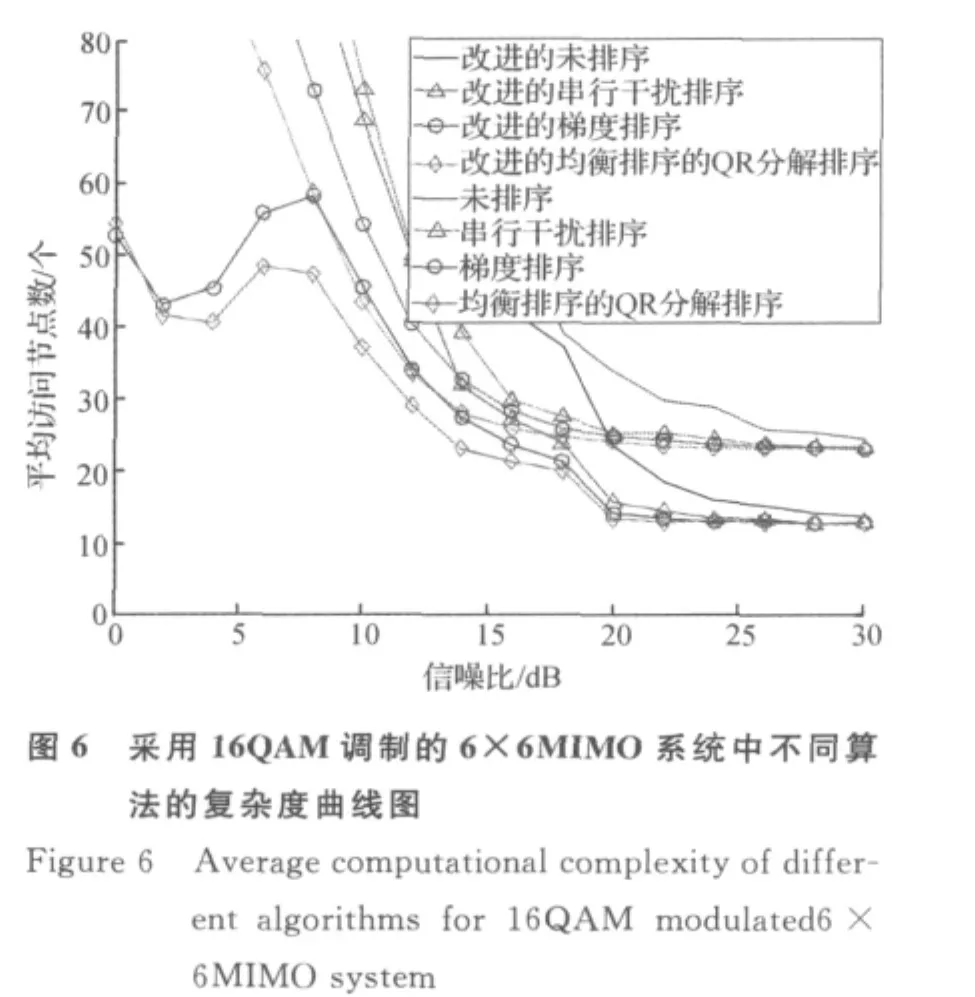
图4为4×4的MIMO系统中采用16QAM星座调制时的复杂度曲线图.从图中可以看出，相比原来的球形解码算法，采用阈值后，各算法的复杂度均有不同程度的降低.在低信噪比范围内，各算法的复杂度降低幅度各不相同，其中GRA算法和BSQR算法的下降幅度较大.在高信噪比范围内，原来的算法在20dB之后展开节点数逐渐收敛于15左右，即为2m－1；而采用阈值后，各算法在20dB之后展开节点数逐渐收敛于8左右，即为树的深度m.图5为4×4的MIMO系统中采用64QAM星座调制时的复杂度曲线图，由于调制阶数较高，此时的复杂度也较高，各算法的复杂度在24dB之后开始收敛，在30dB时原来的算法收敛到16左右；而采用阈值后则收敛到9左右，可以看出，随着信噪比的继续增大，采用阈值后其复杂度最终会收敛于8，即为树的深度m.在低信噪比范围内，采用阈值后，各算法的复杂度也有不同程度的降低.图6为6×6的MIMO系统中采用16QAM星座调制时的复杂度曲线图.同样的，在低信噪比范围内，采用阈值后，各算法的复杂度均有不同程度的降低，而在高信噪比范围内，在20dB之后，原来算法的复杂度逐渐收敛到23左右，即2m－1；而采用阈值后，其复杂度逐渐收敛到12左右，即为树的深度m.以上仿真结果表明，本文所提出的阈值算法有效的将球形解码算法在高信噪比下展开节点数的收敛值从2m－1降到了搜索树的深度m，并且使其在低信噪比范围内的复杂度也进一步得到了降低.

图4 采用16QAM调制的4×4MIMO系统中不同算法的复杂度曲线图Figure 4 Average computational complexity of different algorithms for 16QAM modulated4×4MIMO system

4 结 语

球形解码算法由于其良好的性能被应用到通信系统的诸多领域，但由于SE搜索策略的限制，其在高信噪比下的展开节点数始终收敛于2m－1.本文所提出的算法将其在高信噪比下展开节点数的收敛值降到了m，并且使其在低信噪比范围内的复杂度也得到了相应的降低.在高信噪比范围内，该算法的性能相比原始的球形解码算法有少许差距，但这可以通过对阈值的调整来改善，从而达到性能和复杂度的折中.

［1］郭丽娜，金 宁.瑞利信道下网格酉空时调制的仿真实现［J］.中国计量学院学报，2009，20（2）：163－166.

［2］VIAKALO H，HASSIBI B.On the sphere－decoding algorithm Ⅱ.Generalizations，second－order statistics，and applications to communications［J］.IEEE Transactions on the Signal Processing，2005，53（8）：2819－2834.

［3］DAMEN M O，GAMAL H E，CAIRE G.On maximumlikelihood detection and the search for the closest lattice point［J］.IEEE Transactions on Information Theory，2003，49（10）：2389－2402.

［4］BARBERO L G，THOMPSON J S.Fixing the complexity of the sphere decoder for MIMO detection［J］.IEEE Transactions on Wireless Communications，2008，7（6）：2131－2141.

［5］DING Y H，WANG Y，DIOURIS J F.Robust fixed complexity sphere decoder［C］／／IEEE Global Telecommunications Conference.［s.l.］：IEEE，2010.

［6］WOLNIANSKY P W，FOSCHINI G J，GOLDEN G D，et al.V－BLAST：An architecture for realizing very high data rates over the rich－scattering wireless channel［C］／／in Proc URSI International Symposium on Signals，Systems and Electronics（ISSSE 98）.Atlanta：IEEE，1998：295－300.

［7］WIESEL A，MESTRE X，PAGES A，et al.Efficient Implementation of sphere demodulation［J］.IEEE Workshop on Signal Processing Advances in Wireless Communications，2003，4：36－40.

［8］DAI Y M，YAN Z Y.Memory－constrained tree search detection and new ordering schemes［J］.IEEE Journal of Selected Topics in Signal Processing，2009，3（6）：1026－1037.

［9］WU X B，DAI Y M，YAN Z Y，et al.Improving the reliability of the k－best algorithm for MIMO detection with ordering［C］／／Wireless and Optical Communications Conference.［s.l.］：IEEE，2010.

［10］WU X B，DAI Y M，WANG Y，et al.Efficient ordering schemes for high－throughput MIMO detectors［J］.Journal of Signal Processing Systems，2010，64（1）：61－74.

［11］SHAYEGH F，SOLEYMANI M R.Low complexity implementations of sphere decoding for MIMO detection［C］／／Electrical and Computer Engineering. Canada：IEEE，2008：821－825.

［12］李庆坤，马红光，李 正，等.一种低复杂度的MIMO预处理球形译码算法［J］.信号处理，2009，25（12）：1867－1870.

［13］TRUJILLO R A，GARCIA V M，VIDAL A M，et al.A gradient－based ordering for MIMO decoding［C］／／Signal Processing and Information Technology.［s.l.］：IEEE，2009.