非规则几何结构阵列下的宽带线性调频信号波达方向估计
2011-08-01刘开华黄翔东于洁潇
罗 蓬,刘开华,黄翔东,于洁潇
(天津大学电子信息工程学院,天津 300072)
线性调频(linear frequency modulation,LFM)信号是一类重要的非平稳信号,被广泛地应用于雷达、声纳和通信等信息系统中,针对此类信号的波达方向(direction of arrival,DOA)估计问题也逐渐成为阵列信号处理领域的研究热点之一.由于 LFM 信号具有宽带非平稳的特性,其阵列方向矩阵与时间相关,因此常规的子空间算法不再适用于这类信号的 DOA估计.为了解决上述问题,比较常用的思路是:首先利用各类时频分析工具对阵列输出数据进行预处理,然后通过合理的时频点的选取,构造时频相关矩阵代替传统的阵列相关矩阵,最后利用 MUSIC、ESPRIT等信号子空间算法实现 DOA估计.沿着这个方向,已经出现了很多比较成熟的方法[1-3],其中以国内学者陶然、齐林及其科研团队提出的基于分数阶Fourier变换(fractional Fourier transform,FRFT)的LFM 信号 DOA 估计方法[4-6]受到了最多的关注.由于FRFT是一种一维的线性变换,与常用的二次型时频分布相比,它不受交叉项的困扰,而且可以理解为LFM基分解,所以非常适合对LFM信号的处理.
传统的基于FRFT的DOA估计方法是针对规则几何结构阵列的.在实际的应用环境中,由于设备内部空间以及阵列资源的限制,要保证阵列几何形状的均匀和规则必然会降低有限资源的利用率,最终导致参数估计性能的下降.另外,由于阵列校正技术的限制,要保证阵列结构的严格规则也是十分困难的.
笔者对非规则阵列的结构以及分数阶Fourier域阵列数据模型进行了深入分析,提出了一种宽带LFM信号的DOA估计方法,该方法不受阵列结构的限制,具有估计精度高、鲁棒性强等优点.
1 阵列结构和信号模型
考虑如图 1所示的非规则阵列结构,该阵列由M+1个阵元组成.不失一般性,令第 1个阵元为参考阵元,并将其位置设为坐标原点,所有阵元按各自横坐标的大小依次编号表示,k=1,2,…,M+1.假设远场有P个LFM信号入射到该阵列上,为避免混淆,在后面的叙述中,以变量的下标区分各入射信号,上标区分各阵元.则第k个阵元的输出为
式中:sq(t)为第q个入射LFM信号;fq、μq分别为该信号的中心频率和调频率参数;nk(t)为第k个阵元上的高斯白噪声,这里假设各入射信号之间、各阵元上噪声之间以及信号和噪声之间均不相关;τqk是第q个信号在第k个阵元相对于参考阵元的延时,由几何关系得
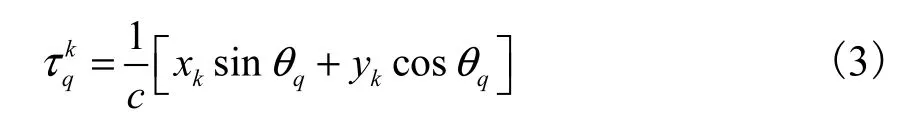
式中:c表示光速;(xk,yk)为第k个阵元的位置坐标;θq为第q个信号的入射角.

图1 非规则几何结构阵列示意Fig.1 Schematic diagram irregular geometry array
需要说明,图1所示的非规则阵列实际上已成为一个二维阵列,但是只考虑信源的方位角一维 DOA估计,因为研究非规则阵列上的 DOA估计问题在该信号模型下已具有足够代表性,且文中方法可以很容易推广到任意结构面阵的二维 DOA估计中,故不予赘述.
2 提出的LFM信号DOA估计方法
2.1 阵列信号的分数阶Fourier变换
一个信号x(t)的旋转角度为α的FRFT定义为

式中:p为 FRFT 的阶,可以为任意实数; Kα(t,u)为变换核函数,α=pπ/2,有
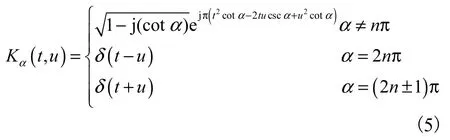
相应的FRFT逆变换为

式(6)中说明信号x(t)可被分解为u域上一组正交的LFM 基的线性组合,u域一般称为分数阶 Fourier域,时域和频域可分别视为α=0与α=π/2的特例.
考察参考阵元上接收到的第 q个 LFM 信号sq(t),对其进行角度为 α 的 FRFT得到 Sq(α,u),直接利用文献[7]的结论,可知 Sq(α,u)在(α,u)平面上将形成一个能量聚集的谱峰,而该谱峰的位置为
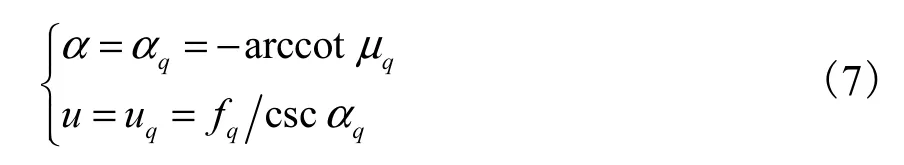
实际应用中,一般只能对有限长数据样本做离散形式的分数阶Fourier变换(discrete fractional Fourier transform,DFRFT).选用了文献[8]提出的分解型快速算法,该算法的计算结果与连续的FRFT的输出比较接近,而且可以利用FFT来实现,计算的复杂度为O(Nlg N).但是该算法首先对输入数据进行了量纲归一化处理,使得归一化以后的 LFM 信号的参数发生了改变,所以需要根据归一化前后信号参数之间的关系对理论公式进行修正,才能和实际结果保持一致.这部分的相关内容文献[9]中已有详细描述,本文中不再赘述.直接利用相关结论,将式(7)修正为
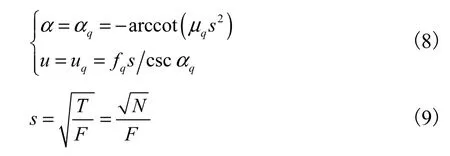
式中:s为量纲归一化因子;T表示信号的观测时间长度;F表示采样频率;N表示信号的快拍数.
由式(8)可知,一个 LFM 信号的能量聚集域变换角度取决于该信号的调频率,而在该域上的谱峰位置取决于信号的调频率和中心频率.相应地可以求出Sq(α,u)的峰值谱线取值为
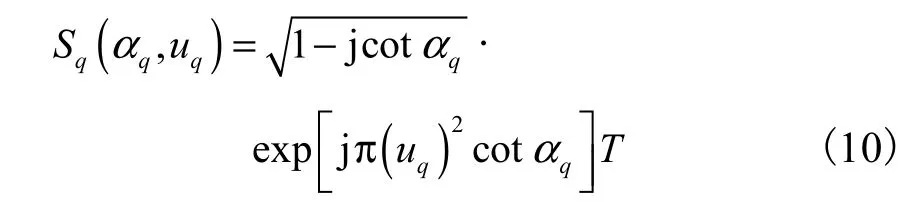
另外,由式(1)和式(2)可知,信号 sq(t)传播到第k个阵元时的表达式为


比较式(10)和式(14),可得 sq(t)在参考阵元和第 k个阵元上的输出的分数阶Fourier域峰值变化情况

式中

2.2 基于FRFT的阵列空间时频输出以及广义旋转,矩阵
对式(1)两端进行FRFT,由于FRFT是一种线性变换,根据其可加性,可得第k个阵元上所有P个入射信号的叠加输出的FRFT

由于各入射信号间相互独立,所以它们在(α ,u )平面上出现峰值的位置均不相同.在第q个信号对应的峰值点处,其他信号均未达到能量聚集,因此,式(17)可以化简为

故实现了各入射LFM信号的分数阶Fourier域分离,简化了数据模型.
选择分数阶Fourier域上P个峰值点数据作为该阵元上观测数据,则第k个阵元上的空间时频输出为
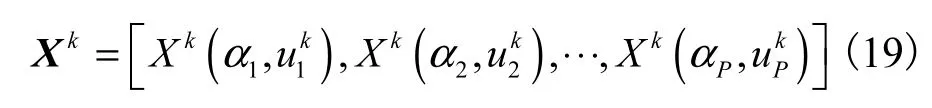
将所有阵元的空间时频输出表示为向量形式
式中
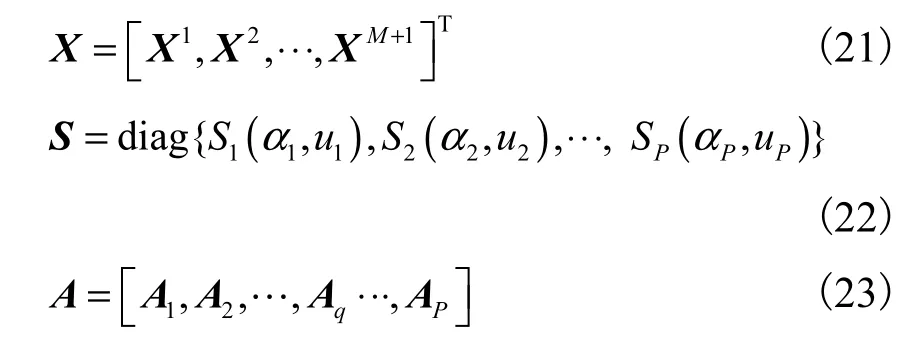
式中
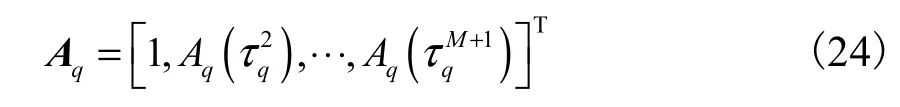
为第q个LFM信号的分数阶Fourier域方向向量.根据式(16)可知,在阵列结构固定的前提下,该向量只与第q个信号的入射角有关.
根据ESPRIT算法的思想,将M+1个阵元分成两个相互重叠的子阵列,其中前 M 个阵元组成子阵a,后 M 个阵元组成子阵 b.将两个子阵的空间时频输出表示为向量形式

式中Aa和Ab分别为两个子列的分数阶Fourier域方向矩阵,与A的关系

式中:L1为矩阵的第 1行;Ln为矩阵的最后 1行.由于两个子列间存在固定的几何关系,所以可以通过定义旋转矩阵的方法来反映两个子列间的信号空间关系.令

则有
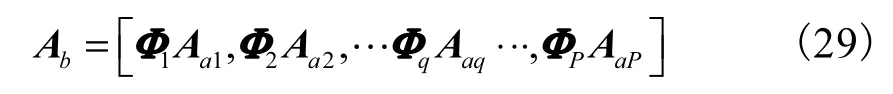
式中

定义为第 q个入射信号在两个非规则子阵上的分数阶Fourier域广义旋转矩阵.
2.3 基于谱峰搜索的广义ESPRIT算法
考虑阵列空间时频输出数据的协方差矩阵
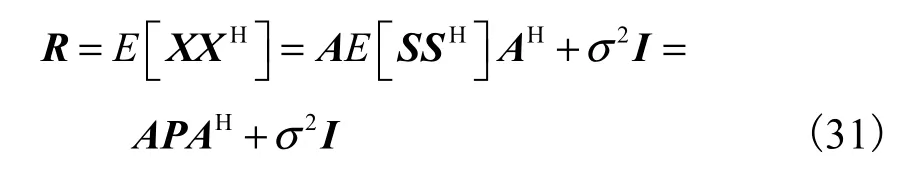
式中 E [⋅]表示统计期望.对R进行特征值分解,即
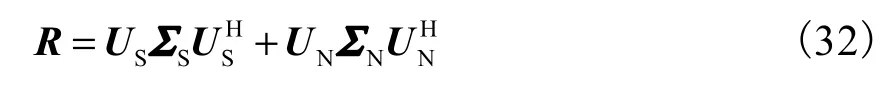
式中 ΣS和 ΣN为两个对角阵,分别由 R的信号子空间和噪声子空间的特征值构成;US和UN由特征值对应的特征向量构成.
矩阵US可以表示为

显然Ua和Ub分别对应于子阵a和b. 若信源协方差矩阵 P是非奇异的,则阵列方向矩阵 A与阵列输出的协方差矩阵的信号特征向量组成的子矩阵US所张成的迹空间相同,即有

式中 T是一个 P×P的满秩矩阵.比较式(27)和式(33),即

定义矩阵
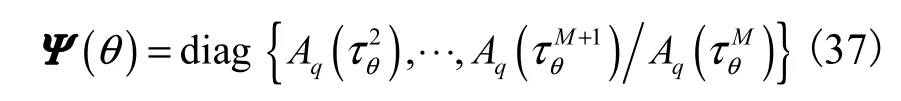
式中()kqAθτ可由式(16)计算得到,而kθτ可由下式获得,即
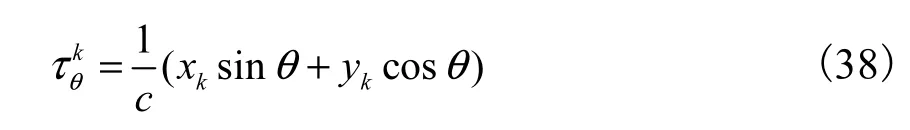
于是可以构造矩阵
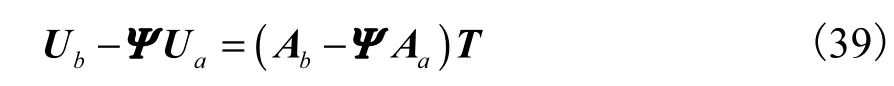
将式(29)代入式(39)得
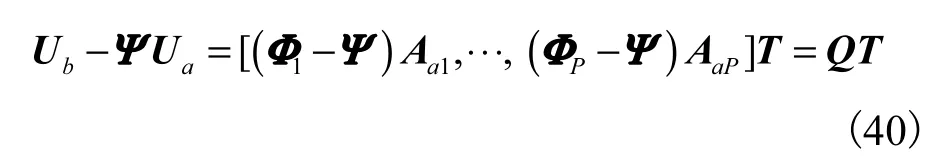
当θ=θq时,矩阵Q的第q列等于零,将会造成矩阵 Ub−ΨUa的亏秩.矩阵Ub−ΨUa为一个M×P的矩阵,将其左乘一个P×M的满秩矩阵则可通过式(41)的函数的谱峰搜索实现对第q个LFM 信号的入射角θq的估计.
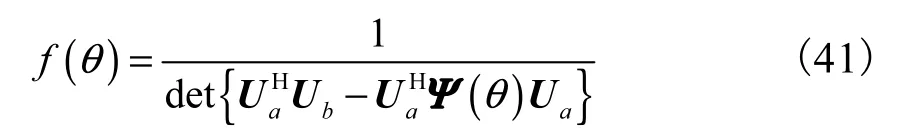
2.4 算法的实施步骤和细节
通过分析,将算法的具体步骤总结如下.
(1) 对参考阵元上接收的信号做连续变化阶次的 FRFT,并对平面做二维搜索,通过谱峰个数估计出入射信号的个数P,并将各谱峰位置记录下来.
(2) 取各个阵元上接收信号的关于角度qα的FRFT并做一维搜索,得到各个阵元上第q个信号对应的谱峰位置以及峰值点的数据
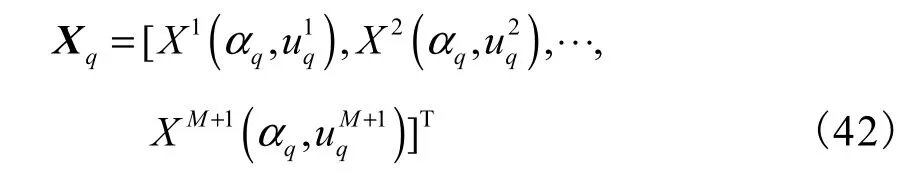
(4) 对 Rq进行特征值分解,得到信号特征向量组成的矩阵 US,构造式(41)所示的谱函数 f (θ) .
(5) 遍历角度θ,对 f (θ)进行峰值搜索,即可得到第q个LFM信号的入射角θq的估计.
(6) 重复步骤(2)~(5),直至估计出所有入射信号的波达方向角.
需要指出的是,该方法利用不同阶次的FRFT对各入射 LFM 信号进行分离,然后逐一估计出它们的DOA参数,因此该方法无需额外的参数配对过程,且可估计出的 DOA数目不受阵列孔径的限制.然而该方法的一个适用前提是各入射信号之间相互独立,当入射信号的数目过多时,信号间的参数较为接近、相关性增大,所以在分数阶 Fourier域峰值提取过程中很难区分不同的入射信号,最终导致算法性能的下降.
3 与传统FRFT-ESPRIT算法的关系
考虑本文方法的一种特殊情况.假设阵列为一均匀线阵,此时入射信号在各个阵元上的延时保持一个等差关系,即
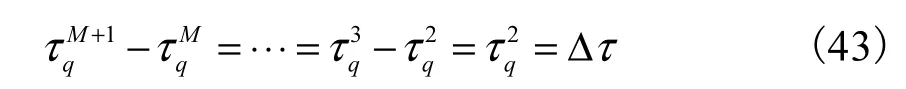
文献[5]提出将式(16)近似为
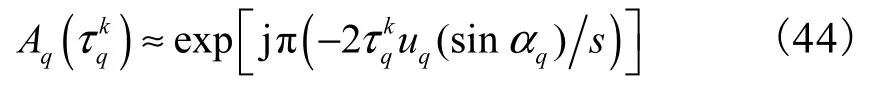
综合式(30)、式(43)和式(44),可知 ULA 情况下,广义旋转矩阵 Φq的对角线上的元素均相等,Φq退化为一个标量,即

此时,两个子列的方向矩阵之间的关系可表示为

式中Φ 通常被称为旋转矩阵,具有

4 仿真实验
假设非规则阵列由 10个阵元构成.两个相互独立的等幅宽带 LFM 信号分别以入射角 θ1=25°和θ2=-40°入射到该阵列上,两个信号的初始参数分别设定为:f1=-12,MHz、μ1=1,MHz/μs、f2=9,MHz、μ2=-0.7,,MHz/μs.采样频率为 100,MHz,快拍数为501.阵元噪声为零均值高斯白噪声.
图2为参考阵元上观测信号的连续变化阶次FRFT的二维扫描谱,信噪比取10,dB.从图2中可以看出,在(p,u)平面上有两个明显的谱峰,分别对应于两个入射LFM信号.
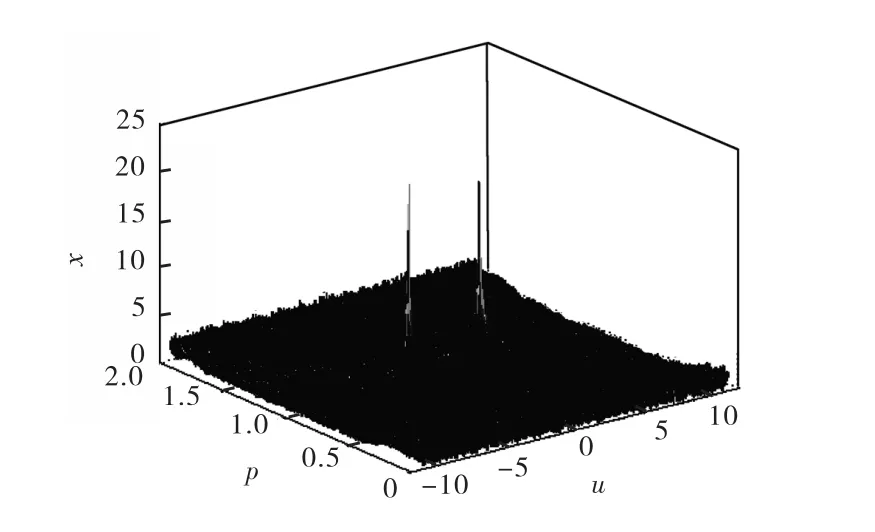
图2 入射信号的二维FRFT扫描谱Fig.2 2D FRFT scan spectrum of incident signals
按照所述方法,分别构造这两个信号在分数阶Fourier域上的广义ESPRIT空间谱,如图3所示.
对图3(a)和(b)所示的两个谱函数做关于角度θ的一维谱峰搜索,选择扫描步长为 0.01°,得到两个入射信号的DOA估计
本文方法的DOA估计均方根误差θRMSE随信噪比变化曲线如图4所示,其中DOA估计的RMSE计算公式为
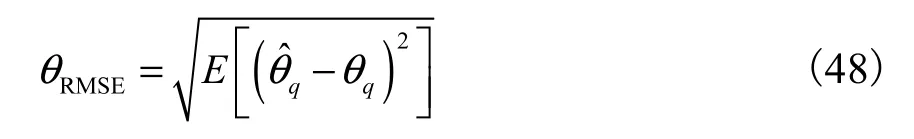
另外,图 4中还给出了本实验中两个信源 DOA估计的确定性克拉美罗界(Det-CRB)[10].所有仿真结果均为50次独立实验的平均.
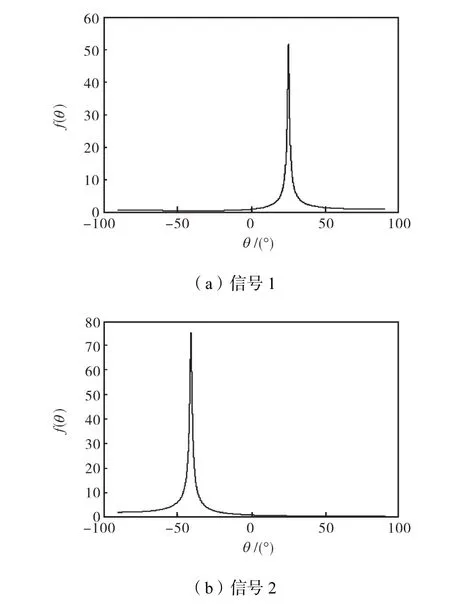
图3 入射信号的广义ESPRIT空间谱Fig.3 Generalized ESPRIT spatial spectrum of incident signals
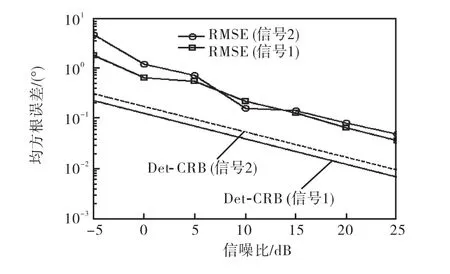
图4 DOA估计的RMSE和CRB随SNR变化曲线Fig.4 DOA estimation RMSE and CRB versus SNR
从图 4中发现,随着信噪比的不断增大,本文方法的 DOA估计 RMSE逐渐逼近确定性 CRB,证明了本文方法的有效性.
5 结 语
文中提出了一种基于 FRFT和广义 ESPRIT算法的宽带 LFM 信号 DOA估计方法.该方法可以在非规则阵列条件下实现多个 LFM 信号的 DOA估计,且具有较高的精度.分析可知,本文方法是传统FRFT-ESPRIT算法在非规则阵列上的广义形式.通过仿真实验的结果,并考虑到现有的FRFT离散化算法本身存在的误差,本文方法的 DOA估计误差在工程实践的可接受范围内.
[1] Wen Zhong,Li Liping,Chen Tianqi,et al. Joint multiple parameters estimation for coherent chirp signals using vector sensor array[J]. Science in China:Ser F,2008,51(1):93-100.
[2] Zhou Xin,Shi Yaowu,Yang Wenhong. 2D DOA and polarization estimation of LFM signals with one electromagnetic vector sensor[C]// International Conference on Signal Processing. Beijing,China,2008:386-389.
[3] 李立萍,黄克骥. 基于STFT的相干宽带调频信号2D到达角估计[J]. 电子与信息学报,2005,27(11):1760-1764.Li Liping,Huang Keji. 2D DOA estimation of coherent wideband FM signals based on STFT[J]. Journal of Electronics and Information Technology,2005,27(11):1760-1764(in Chinese).
[4] 陶 然,周云松. 基于分数阶傅里叶变换的宽带 LFM信号波达方向估计新算法[J]. 北京理工大学学报,2005,25(10):895-899.Tao Ran,Zhou Yunsong. A novel method for the direction of arrival estimation of wideband linear frequency modulated sources based on fractional Fourier transform[J]. Transactions of Beijing Institute of Technology,2005,25(10):895-899(in Chinese).
[5] 杨小明,陶 然. 基于分数阶 Fourier变换和 ESPRIT算法的 LFM 信号 2D波达方向估计[J]. 兵工学报,2007,28(12):1438-1442.Yang Xiaoming,Tao Ran. 2D DOA estimation of LFM signals based on fractional Fourier transform and ESPRIT algorithm[J]. Acta Armamentarii,2007,28(12):1438-1442(in Chinese).
[6] Qu Haitao,Qi Lin,Mu Xiaomin,et al. DOA estimation of coherent wideband LFM signals based on fractional Fourier transform[C] // International Conference on Innovative Computing,Information and Control.Beijing,China,2006:6-9.
[7] Qi Lin,Tao Ran,Zhou Siyong,et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China:Ser E,2003,33(8):749-759.
[8] Ozaktas H M,Arikan O,Katuy M A,et al. Digital computation of the fractional Fourier transform[J]. IEEE Transaction on Signal Processing,1996,44(9):2141-2150.
[9] 赵兴浩,邓 兵,陶 然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报,2005,25(4):360-364.Zhao Xinghao,Deng Bing,Tao Ran. Dimensional normalization in the digital computation of the fractional Fourier transform[J]. Transactions of Beijing Institute of Technology,2005,25(4):360-364(in Chinese).
[10] Stoica P,Nehorai A. MUSIC,maximum likelihood,and Cramer-Rao bound[J]. IEEE Transaction on Acoustics,Speech,and Signal Processing,1989,37(5):720-741.
