基于对技术身份密码学的构造方法
2011-08-01刘哲理贾春福李经纬纪鸿舜
刘哲理,贾春福,孙 涛,李经纬,纪鸿舜
(1. 南开大学信息技术科学学院,天津 300071;2. 中国科学院长春光学精密机械与物理研究所,长春 130033;3. 环球磁卡股份有限公司,天津 300202)
基于身份密码学(identity-based cryptograghy,IBC)系统是在公开密钥基础设施(public key infrastructure,PKI)基础上发展而来的公钥加密体制,它简化了数字证书的交换和密钥管理,使安全应用更加易于部署和使用.
Shamir[1]于 1984年首次提出了基于身份加密(identity-based encryption,IBE)的概念,用户的公钥可以使用任何与其身份相关的字符串(如邮件、身份证号、图片等),而对应于该身份的私钥则由私钥生成中心(private key generator,PKG)产生.在 2001年,Sakai等[2]和Boneh和Franklin[3]独立地使用双线性对技术提出了实用的 IBE方案,Cocks[4]也基于二次剩余问题给出了相应的解决方法.对技术可以实现曲线点群间的映射,并且将其中的计算安全性归结到离散对数或其他的一些数学难题上.因此,对技术迅速成为密码学研究应用的重点,拉开了基于对技术的IBE研究序幕,也推动了IBC其他相关领域,如基于身份签名(identity-based signature,IBS)、基于身份的密钥协商(identity-based key agreement,IBKA)和基于身份的签名加密(identity-based signcryption,IBSC)等的研究和发展.
文献[5-9]分别从多角度综述了 IBC的相关研究工作.其中,文献[5]描述了2004年前 IBC各研究领域里提出的使用对技术的典型方案,列举了每个方案所采用的困难性假设、安全性和效率;文献[6]概述了IBE和IBS领域使用对技术的典型方案,总结了非基于身份的几类加密方案与IBE的关联,并分析了IBC的应用前景和开放性问题;文献[7] 围绕安全性和效率等方面,总结了 2004年之前提出的使用因式分解、二次剩余和对技术的数字签名、加密和密钥协商3类IBC领域的典型方案;文献[8]同样从加密、数字签名和密钥协商出发,对基于 IBC的研究现状进行了综述,对其中存在的安全模型、执行效率等问题进行了详细分析;文献[9]概括了 IBE安全性的形式化定义,总结了 IBE安全性之间的相互转化规律以及达到高安全性的转化方法,并从安全性和效率的角度对比了已提出的典型IBE方案.
本文则专注于IBC方案的构造方法研究,沿用文献[10]中基于对技术的IBC方案的构造分类,进一步给出各种构造方法的形式化定义,然后从安全模型、对兼容性、空间和时间效率等多个角度对使用不同构造方法的典型方案做出对比,指出可交换隐藏构造方法是最适合随机预言机模型的消除,且能够产生效率较高的构造方案,是目前发展较快的IBE构建方向.
1 双线性对
双线性对也可以称作双线性映射.假设存在函数映射 e : G1× G2→ G ,其中 G1和 G2是具有p阶的加法循环点群,G是另一个具有p阶的乘法循环点群,g1和 g2分别为 G1和 G2的生成元,如果e满足以下条件,则它是一个可采纳的双线性映射.
(1)双线性:对于任意的a, b∈Z,有e( a g1, b g2)=
(2)非退化性:e ( g1,g2) ≠ 1∈G,即e( g1, g2)为G的一个生成元.
点群 G1和 G2被称为双线性点群,G为目标点群,且点群的选取均基于椭圆曲线[11].
许多 IBE方案的构造过程中使用的双线性对为对称对,即 G1=G2,e: G1× G1→ G .这种假设的优点是可以简化一些对应的符号表示,缺点是具有一定的局限性,更可取的方法是使用非对称对,对于 IBE方案的构建往往更加紧凑和有效.Galbraith等[12]提出了一种合理的对分类方法,对于同构计算 φ : G2→G1和它的逆 φ−1有3种类型:
(1)如果φ和 φ−1都是有效可计算的,称为对称对;
(2)如果只有φ是有效可计算的,称为弱非对称对;
(3)如果φ和 φ−1都是非有效可计算的,称为强非对称对.
虽然 G1和 G2可以相同,但是目标点群G必须区别于 G1和 G2,且映射到目标点群G上的点是不能映射回点群 G1和 G2上的,这也是构建过程中数学难题和复杂性假设的基础.
2 3类IBE方案的构造
下面给出IBE方案的一般化抽象形式,通常由以下4步算法组成.
(1)Setup(k):输入安全参数 k,输出用于加解密过程的公共系统参数params.
(3)Encryption(M,params,ID):输入待加密消息M、系统参数params和公钥ID,输出密文C.
(4)Decryption(C,params,dID):输入密文 C、系统参数params和私钥dID,输出明文M.
基于身份密码学系统的研究主要由安全性和效率2个方面不断推动向前发展,实际应用中要求设计出高安全性和高效率的密码学方案.自 2001年以来,国内外学者提出了大量使用对技术的 IBE方案,这些方案从构造方法角度主要分为3类:身份域哈希(identity-domain-Hash)IBE方案、指数逆(exponentinversion)IBE方案、可交换隐藏(commutative-blinding) IBE方案.本节首先介绍3类方案的构造特征,之后从对兼容性、安全模型、时间和空间效率方面研究分析3类方案的特性.
2.1 身份域哈希IBE方案
身份域哈希IBE方案的构建特征比较直接,主要思想为基于身份的密钥抽取,可形式化地描述如下:
(1)Setup(k) 选择一个密码学相关的哈希函数H ( ),且该函数需定义为一个随机预言机,主密钥α;
(2)Extract(msk,ID) 使用哈希函数 H ( )将身份域中的一个任意身份字符串 ID ∈{0,1}*映射到一个双线性点群H(ID)∈G上,对应于公钥身份ID的私钥为αH (ID);
(3)Encryption(M,params,ID) 使用 H ( ID)参与加密运算;
将式(3)、(9)代入式(10)、(11)可得空间光到少模光纤耦合效率随横向偏移rb的变化曲线.由于两模光纤的模场面积较单模光纤大,且支持三个模式的模场传输,当聚焦光斑发生横向偏移时,两模光纤的LP11a模和LP11b模也会接收到信号光,少模光纤接收到的光能量要高于单模光纤,能够获得更高的耦合效率,因此少模光纤对光斑横向偏移的容忍度更高.
(4)Decryption(C,params,dID) 使用αH(ID)参与解密运算.
这类方案的典型代表为 BF-IBE[3]、GS-HIBE[13]和 Yao-HIBE[14],它们通常利用巧妙的数学构造,比如通过构建一个形式为 e( g, H ( ID))αr(其中α为主密钥,r为发送者选取的短期随机加密数)的内部会话密钥,基于双线性对的特性,完成加解密的运算.
这类构造方法的构建和安全性证明过程比较简单,而且在使用密码学哈希函数(如MD5,SHA)代替随机预言机模型的情形下,实用性较高.但是这类方案的缺点也很明显,一个缺点在于广泛地使用了建模成随机预言机的密码学哈希函数,而且假设哈希值均匀地分布在双线性点群上,由于不可能总是不使用任何离散对数的知识来均匀抽样或哈希到合适的子群,因此潜在限制了生成点群曲线的选择.另一个缺点将表示身份的字符串直接哈希到曲线点群上的开销较大,且加密过程通常需要一个不可避免的对计算,因此效率有待提高.
2.2 指数逆IBE方案
指数逆 IBE方案的思想是基于 Mitsunari等[15]提出的一种假设类型,即任何出现在一个点群元素指数上的系数都难于计算它的逆.如给定g和gx,很难计算出 g1x.
这类IBE方案的主要构造思想描述如下:
(1)Setup(k) 选定生成元g和随机数x,计算gx并将其作为公开参数的一部分,x作为主密钥的一部分或者由其产生主密钥;
(2)Extract(msk,ID) 将身份ID与x编码为整数域的某数值(表示为 h ( ID,x)),对应于公钥身份ID的私钥可表示为形如 g1h(ID,x)的表达式;
(3)Encryption(M,params,ID) 使用ID参与加密运算;
(4)Decryption(C,params,dID) 使用 g1h(ID,x)形式的私钥参与解密运算,由于对运算的性质,通过计算 gx和 g1x,可以很容易地消除指数,而不泄漏x.
这类方案的典型代表为 SK-IBE[16]、Chen-IBE[17]、BB2-IBE[18]和 Gentry-IBE[19].为了实现这类IBE方案,需要将身份编码为x的一部分,然后设计一个过程使得 gx可以由公共参数和相关信息计算得出,而 g1x可以由一个保密的陷门计算出来.利用对运算的性质,通过计算 gx和 g1x来消除指数,进而可以应用到IBE方案的加解密数学构造中.
这种指数逆思想的优点是不再需要将身份直接哈希到一个可利用对计算的点群,而只需要通过简单操作将身份哈希到一个整数点群 Zp上,效率就有所提高.缺点是这类指数逆方案的安全性证明都比较复杂,通常需要设计和准备很多复杂的因子,而且要求能够通过变换和约简满足安全性证明过程中各类查询的形式化要求.一个典型的假设如 k-BDHI,给定多项式序列元素 N , y N, y2N,… ,ykN,难于计算e( N , N )1y.序列长度由参数k决定,且至少与私钥拥有者的最大数目相同.因此k值对于证明来讲必须足够大,但是假设的可靠性就会相应降低.
2.3 可交换隐藏IBE方案
可交换隐藏方案是最近出现的 IBE方案构造思想,主要思路是从2个或更多的保密系数中创建2个难于判断的因子,用于对计算下的互相交换.
这类IBE方案的主要构造思想描述如下:
(1)Setup(k) 选取随机数α,α作为主密钥的一部分,一般随机选取双线性点群上的点g0∈G,以为主密钥;
(2)Extract(msk,ID) 将身份ID与主密钥根据特定的私钥生成算法产生身份ID对应的私钥,通常由几部分组成,即 dID= ( d1,⋅⋅⋅,dn) ,而且每部分一般是指数形式,可以与主密钥 gα0相关,也可以引入随机数作为指数;
(3)Encryption(M,params,ID) 选取随机数r,r将作为一次加密过程中所使用的会话密钥参与加密运算,使用身份ID和会话密钥r加密产生的密文通常由几部分组成,密文的每部分一般以r作为指数,即C = ( c1,⋅⋅⋅,cn) = ( []r, ⋅⋅⋅,[]r);
(4)Decryption(C,params,dID) 将私钥与密文各部分参与解密运算,解密运算通常是由于密文C和私钥的每部分都是指数形式的数值,因此利用对运算的性质,可以巧妙地消除指数,而不泄漏α.
BB1-IBE[18]是最早提出的这类方案,该方案回避了早期方法的大多数问题.BB1-IBE方案类似于“指数逆方案”,将身份作为整数编码;而安全约简同“身份域哈希方案”相似,利用了BDH(bilinear Diffie-Hellman)复杂性假设.这类方案最好的性质是其代数结构所提供的较好适应性.而且在数量和对基本 IBE概念的扩展变化上迅速超过了前面 2种方案.这类方案的典型代表为 BB1-IBE[19]、Waters-IBE[20]、Naccache-IBE[21]和 Waters09-IBE[22].
3 对兼容性
在前面介绍中已经看到对可以分为3种类型:①对称对;②弱非对称对,支持一种从 G2→G1的单向映射;③非对称对,且双线性点群 G1、G2之间不存在高效的相互映射.如果没有有效的单向或双向映射,一些方案将无法构造,有些方案也会因为这些映射的存在变得不够安全,还有些方案无论这类同构是否存在,都会用理想的方式收集 G1和 G2间的密码学数据.此外,一些建模为随机预言机的哈希函数可能很难找到对应实例,这主要是由于并非所有的曲线类型都可以直接映射到双线性点群上.上述对类型中,类型①和类型③的曲线通常支持哈希;而类型②的曲线,直接哈希仅可以映射到有效可计算同构的值域上(如果存在 G2→G1的同构,则哈希映射到G),这对那些要求直接哈希到双线点群 G2的方案来说可能是一个问题(哈希到整数循环群比较容易,通常不需要考虑曲线的选择).
从表 1中可以看出身份域哈希方案要求直接哈希到点群G的能力,但是不要求 G1和G之间的同构.指数逆方案中的 Chen-IBE方案为了安全性约简,要求 G2→G1的有效同构.而可交换隐藏方案对双线性点群的要求最低,不要求必须存在哈希到点群的映射或者高效的可计算同构,主要是因为这类构造方案不基于随机预言机模型,并且将身份等信息隐藏到点群生成元的指数运算中.

表1 3类IBE方案的对兼容性比较Tab.1 Comparison of pairing compatibility among three types of IBE schemes
4 安全模型
安全性定义是一个密码学方案关注的重要目标,安全性的高低直接决定了一个密码学方案的安全强度.针对 IBE方案的标准安全模型为适应性选择密文安全(IND-ID-CCA).而在安全性证明过程中,通常关注安全性约简是在标准模型还是理想化模型(随机预言机模型)下达到的.虽然应该尽量避免使用理想化的随机预言机模型,但是在实际应用中通常利用一些性能较好的密码学哈希函数(如 MD5、SHA)来代替随机预言机模型.这种替代会带来安全性的下降,但同时从实用性出发,具有比标准模型下达到同等安全性方案更高的效率,而且安全性证明过程更加简单直接.
文献[9]中总结过的各种数学复杂性假设是安全性证明的基础,大多数复杂性假设都是基于双线性点群的,一部分已被应用于构建实际的IBE系统.这些假设可以进一步分为“非温和”假设和“温和”假设.“非温和”假设,比如 BDHI(bilinear Diffie-Hellman inversion)假设,需要一个大的参数值k,k值需要随着攻击者的查询次数增加,导致问题实例增大,实用性和可测试效率下降.“温和”假设,比如BDH假设,不需要依赖于对手的能力,可测试效率更高.此外,标准模型下的不可区分性约简通常要求使用假设的判定版本,而计算版本通常足以满足随机预言机模型下的约简,这也是使用哈希函数进行安全性约简的一个容易忽略的优点.
表 2中的方案大都满足了选择性密文安全的要求,这也是 IBE方案的标准安全模型,其中 BB1-IBE和 BB2-IBE是在弱于标准安全模型的适应性选择身份攻击下的安全模型.但是表 2中各类方案的安全性约简所依赖的复杂性假设却不完全相同.

表2 3类IBE方案的复杂性假设和安全性比较Tab.2 Comparison of complexity assumptions and security among three types of IBE schemes
从表 2中可以看出,一些方案(如身份域哈希方案)由于对选择密文安全和抗身份冲突等安全性的要求,对随机预言机模型的依赖很强.这类使用了随机预言机模型的方案,都是基于各类假设的计算版本(如 BDH假设),目前对这类方案还没有可证明不使用随机预言机模型的安全性.而不使用随机预言机模型的方案,大都基于各类假设的判定版本,如DBDH(decision bilinear Diffie-Hellman)假设.如指数逆方案的构建对随机预言机模型的依赖较弱,主要视具体构建过程而定.可交换隐藏方案是最适合消除随机预言机模型的方案.
5 时间和空间效率
对于密码学方案较好的比较准则是时间和空间的效率,能够从应用角度直观地衡量出一个方案的效率高低和适用性.主要衡量指标包括方案中各主要步骤的计算时间以及所生成的密钥和密文大小.在实际应用中,这种比较通常与应用环境紧密相连.如方案各步骤的计算时间一般要比密钥和密文的大小更重要,而那些无线或带宽受约束的应用环境却恰恰相反.
5.1 时间效率
基于对的 IBE方案的时间开销主要集中在抽取、加密和解密 3个步骤.主要涉及到的操作包括:对运算时间P,点群 Gi上的求逆运算时间 Ri,点群Gi上的指数运算时间 Ei,点群 Gi上的数乘运算时间sMi,点群 Gi上的乘法运算时间 g Mi,映射到椭圆曲线点群的哈希运算时间MtP.其中,目标点群G上令i为空.其他的符号还有:HIBE中层次化实体的层数l,实体身份ID的长度n.
以BF-IBE方案为例,其Extract算法为:给定身份ID∈{0,1}*,首先计算Q = H ( ID)∈ G ,即通过一个
ID哈希运算将身份映射为椭圆曲线点群上的点 QID,然后执行点群G上的数乘运算 s QID来输出私钥.可见,BF-IBE方案的 Extract算法的时间开销为一次映射到点群的哈希运算,一次点群上的数乘运算,即1M tP + 1 sM1.以此类推,得到 3类主要的基于对技术IBE方案的时间开销,如表3所示.

表3 3类IBE方案的时间效率比较Tab.3 Comparison of time efficiency among three types of IBE schemes
5.2 空间效率
衡量基于对技术 IBE方案空间开销的指标主要为各类点群上参数的个数,包括系统参数的个数、主密钥个数、私钥个数和密文空间.其中l为 HIBE中层次化实体的层数,h为二叉树的高度,n为实体身份ID的长度.
以BF-IBE为例,主密钥为 s ∈Z*q,因此主密钥在点群上的参数个数为 1;系统参数为其中q是点群 G1和 G2的阶,e~是双线性映射取整数数值,P是点群 G1上的一个点,即 P ∈G1,Ppub=sP∈ G1,H1和 H2是 2个哈希函数,H2:G2→ { 0,1}n,因此系统参数在 G1点群上的参数个数为 2,分别为P和 Ppub;身份ID所对应的私钥为sQID=s⋅ QID=s⋅ H1( ID)∈ G1,因此私钥在 G1点群上的参数个数为 1.加密过程产生的密文为 C = 〈rP,其中r∈Z*q,可见密文空间为 G1× { 0,1}n.以此类推,得到3类主要的基于对技术IBE方案的空间开销,如表4所示.
表 3和表 4从时间和空间效率对几类方案的典型代表进行了总结,可以看到,身份域哈希方案由于在构造过程中使用了随机预言机模型,方案的构建效率明显高于其他 2类方案,更适合实际应用.但由于在真实世界中随机预言机模型并不存在,实现时只能使用相关的密码学哈希函数代替,始终存在着安全性降低的隐患.指数逆方案基本可以不使用随机预言机模型进行构建,但是由于这类方案的数学基础复杂性较高,导致系统初始化时参数较多,密文空间相对较大,产生的方案效率较低,安全性证明过程难度较高.而可交换隐藏方案最适合随机预言机模型的消除,且能够产生效率较高的构造,是目前一个发展较快的IBE构建方向.
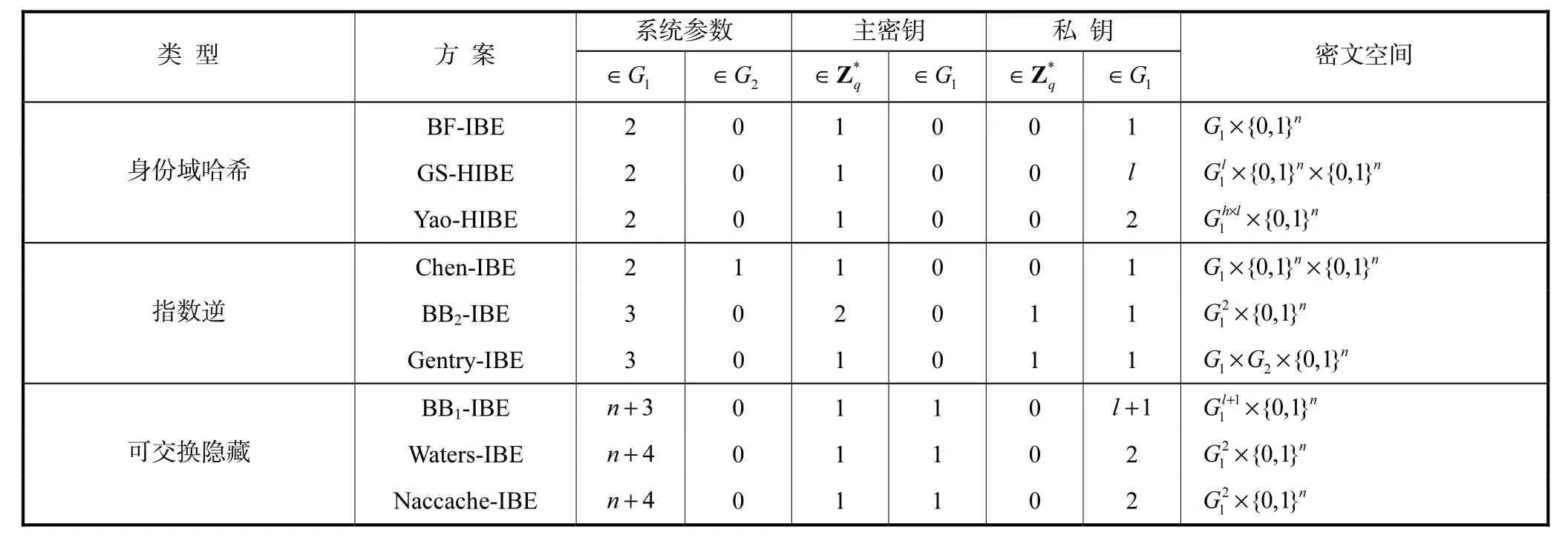
表4 3类IBE方案的空间效率比较Tab.4 Comparison of space efficiency among three types of IBE schemes
6 结 语
根据已有的有关基于对技术的 IBC方案的研究成果,针对身份域哈希、指数逆和可交换隐藏 3类构造方法,提出了各自的形式化定义并分析了优缺点,然后从对兼容性、安全模型、空间和时间效率等多个角度对 3类方法构造的实例做了对比.通过对比分析,可交换隐藏构造方法因为其代数结构所提供的较好适应性,不依赖于随机预言机模型,能够产生效率较高的构造,已经成为目前一个发展较快的 IBE构建方向.
[1] Shamir A. Identity-based cryptosystems and signature schemes[G]. Advances in Cryptology-Crypto’84.Berlin,Germany:Springer-Verlag,1984:47-53.
[2] Sakai R,Ohgishi K,Kasahara M. Cryptosystems based on pairings[C]// Symposium on Cryptography and Information Security(SCIS)2000.Okinawa,Japan,2000:26-28.
[3] Boneh D,Franklin M. Identity-based encryption from the Weil pairing[G]. Advances in Cryptology-Crypto’ 01.Berlin,Germany:Springer-Verlag,2001:213-229.
[4] Cocks C. An identity based encryption scheme based on quadratic residues[C]// Proceedings of the 8th IMA International Conference on Cryptography and Coding.Berlin,Germany:Springer-Verlag,2001:360-363.
[5] Dutta R,Barua R,Sarkar P. Pairing-based Cryptographic Protocols:A Survey[R]. Cryptology ePrint Archive,Report 2004/064. http://eprint. iacr. org/2004/064. 2004.
[6] Baek J,Newmarch J,Naini R,et al. A survey of identity-based cryptography[C]// Proceedingings 10th Annual Conference for Australian Unix User′s Group(AUUG 2004).Canberra,Australia,2004:95-102.
[7] Gorantla M. C,Gangishetti R,Saxena A. A survey on ID-based cryptographic primitives[EB/OL]. Cryptology ePrint Archive,Report2005/094,from http:// eprint.iacr. org/2005/094. 2005.
[8] 田 野,张玉军,李忠诚. 使用对技术的基于身份密码学系统综述[J]. 计算机研究与发展,2006,43(10):1810-1819.Tian Ye,Zhang Yujun,Li Zhongcheng. A survey of identity-based cryptography using pairing[J]. Journal of Computer Research and Development,2006,43(10):1810-1819(in Chinese).
[9] 胡 亮,刘哲理,孙 涛,等. 基于身份密码学的安全性研究综述[J]. 计算机研究与发展,2009,46(9):1537-1548.Hu Liang,Liu Zheli,Sun Tao,et al. Survey of security on identity-based cryptography[J]. Journal of Computer Research and Development,2009,46(9):1537-1548(in Chinese).
[10] Boyen X. General Ad Hoc encryption from exponent inversion IBE[G]. Advances in Cryptology-Eurocrypt 2007.Berlin,Germany:Springer-Verlag,2007:394-411.
[11] Blake I,Seroussi G,Smart N. Elliptic Curves in Cryptography[M]. London:Cambridge University Press,1999.
[12] Galbraith S,Paterson K,Smart N. Pairings for cryptographers[EB/OL]. Cryptology ePrint Archive,Report 2006/165. http://eprint. iacr. org/2006/165. 2006.
[13] Gentry C,Silverberg A. Hierarchical ID-based cryptography[G]. Advances in Cryptology-ASIACRYPT’02.LNCS,2002,2501:548-566.
[14] Yao D,Fazio N,Dodis Y,et al. ID-based encryption for complex hierarchies with applications to forward security and broadcast encryption[C]// ACM Conference on Computer and Communications Security-CCS’04.New York:ACM Press,2004:354-363.
[15] Mitsunari S,Sakai R,Kasahara M. A new traitor tracing[J]. IEICE Transactions on Fundamentals,2002,E85-A(2):481-484.
[16] Sakai R,Kasahara M. ID based cryptosystems with pairing over elliptic curve[EB/OL]. Cryptology ePrint Archive,Report 2003/054.http://eprint. iacr. org/2003/054/.2003.
[17] Chen L,Cheng Z. Security proof of Sakai- Kasahara’s identity-based encryption scheme[EB/OL]. Cryptology ePrint Archive,Report 2005/226.http://eprint. iacr.org/2005/226. 2005.
[18] Boneh D,Boyen X. Efficient selective-ID secure identity based encryption without random oracles[G]. Advances in Cryptology-Eurocrypt’04.LNCS,2004,3027:223-38.
[19] Gentry C. Practical identity-based encryption without random oracles[G]. Advances in Cryptology-Eurocrypt’06. LNCS,2006,4004:445-464.
[20] Waters B. Efficient identity-based encryption without random oracles[G]. Advances in Cryptology-Eurocrypt’05. LNCS,2005,3494:114-127.
[21] Naccache D. Secure and practical identity-based encryption[EB/OL]. Cryptology ePrint Archive,Report 2005/369. http://eprint. Iacr. org/2005/369. 2005.
[22] Waters B. Dual system encryption:Realizing fully secure IBE and HIBE under simple assumptions[G]. Advances in Cryptology-Crypto 2009. Berlin,Germany:Springer-Verlag,2009:595-618.
