增强纤维复合材力学性能指标概率分布类型

吴毅彬，金国芳

(同济大学 结构工程与防灾研究所,上海，200092)

增强纤维复合材料(FRP)的力学性能指标是 FRP应用于土木工程领域中的重要参数之一。各项指标选择的合理以及对其离散型的评价都会直接影响FRP材料工程应用的安全性与经济性。由于钢筋、混凝土等材料本身的离散性较小，性能较稳定，对材料概率统计分布已有一定的研究，因此已广泛应用于设计规范中。目前关于FRP混凝土结构的可靠度研究主要是在对FRP材料概率分布假设的基础上进行，研究表明：非正态分布简化为正态分布带来的可靠度计算误差达20%～30%[1]。FRP材料概率统计分布研究和讨论较少的主要原因在于一方面FRP材性受生产工艺、施工质量、测试方案、破坏形态等因素的影响较为明显，另一方面是FRP生产厂商习惯于将这些数据视为专有，不对外公开，而这些数据又是至关重要的，数据不足可能导致假定的性能参数累积概率分布函数形式不同，这对FRP材料在土木工程中的应用有较大影响。对比已有研究中所采用的分布类型[2-11]可知：FRP材料参数的概率分布类型差异性较大，大多分布类型采用正态分布作为概率分布，这主要是基于经验假设或是建立在钢筋混凝土材料统计分布研究的基础上，由于FRP材料的力学性能与土木工程中长期使用的具有明显弹塑性受力特征的普通低碳钢和混凝土有较大的差别，且FRP材料本身离散性较强，假设的正确性有待验证。同时已有统计参数主要针对材料的拉伸强度，由于纤维复合材的破坏形态有脆性断裂、层间剥离等，因此有必要对其他指标，如弹性模量、厚度等参数进行分析。在此，本文作者通过收集整理近1 000份的FRP材性试验样本，运用参数估计和假设检验方法对材料性能各指标的统计参数和概率分布进行研究，并分析各参数的相关性，在此基础上，重新对指标标准值进行定义、计算，为进一步研究基于可靠度的FRP加固混凝土结构设计方法提供一定理论依据。

1 FRP材性试验研究成果

纤维复合材应用于土木工程阶段，国内外对材料的力学性能指标展开较多的研究[12-17]，但研究结果表明，FPR材料强度与破坏呈现离散性、多层次性、各向开性等特点，影响FRP材料的力学性能不仅与纤维布和胶结树脂紧密相关，且受到施工工艺、工艺水平、施工环境等因素的影响，材料性能离散性较大，各指标统计参数、分布类型较钢材等材料复杂。

本文所选用FRP材料性能测试数据均为根据国内外标准试验方法所进行的试验，部分试验数据由于试验条件如试验环境、仪器等的不同虽存在一定测试偏差，但对影响试验结果的主要条件上基本保持一致性。收集到的国内外近 1 000份的 FRP材性试验样本见表1。

由各指标的统计描述(表1)可知：各组样本的性能指标变化幅度较大，个别数组中最大值为最小值的 2倍多。材料极限抗拉强度随材料体系的不同有明显变化，且与黏贴层数并非呈正比关系，层数越多，片材的拉伸强度反而降低。极限抗拉强度变异系数在0.03～0.23范围浮动。弹性模量对不同材料与层数也呈现出较大差异，弹性模量随着层数增加略有增长，变异系数在 0.03～0.28范围内。试件厚度为平均厚度，厚度小于单层厚度与层数的乘积，表明多层粘贴时存在明显压缩现象，厚度变异系数为0.03～0.13。

由上述3个指标的统计描述可看出：纤维复合材料，特别是现场湿贴型FRP，受纤维布本身质量、树脂性能、周边环境及施工条件等因素的影响很大，因此，在设计阶段应考虑FRP材料的不确定因素，以保证工程安全可靠。

2 概率分布模型与参数估计

Normal分布、Lognormal分布、二参数 Weibull分布和Gamma分布4种分布类型常用于工程中，且较适合于材料模型。每一种分布均可采用概率分布函数(PDF)与累积概率分布函数(CDF)进行描述。

(1) Normal分布

式中：均值-∞＜x，μ＜+∞；标准差σ＞0。

(2) Lognormal分布

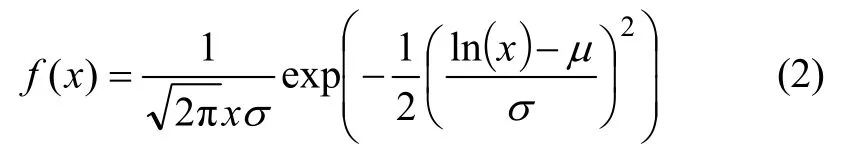
式中：均值-∞＜μ＜+∞；标准差σ＞0；x＞0。

(3) 二参数Weibull分布

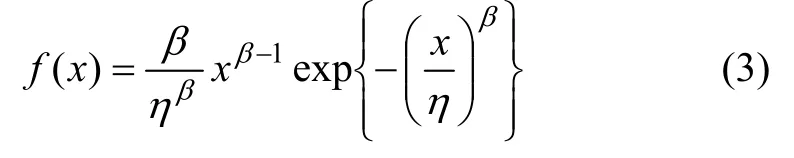
式中：β为形状系数；η为比例系数；η，β＞0；x≥0。

(4) Gamma分布

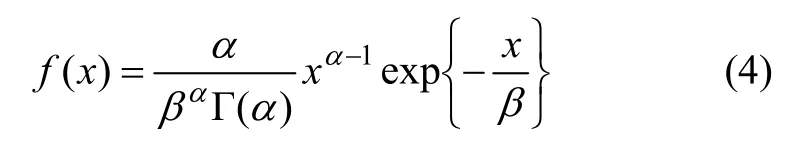
式中：α为形状系数；β为比例系数；α，β＞0；x≥0。

累积概率分布可由函数CDF图进行描述，A1和D1组极限抗拉强度CDF图如图1所示。由图1可知：4种分布类型均可适用于该数组，因此由CDF图无法直观选择最合适的类型分布，其他数组也存在类似情况。

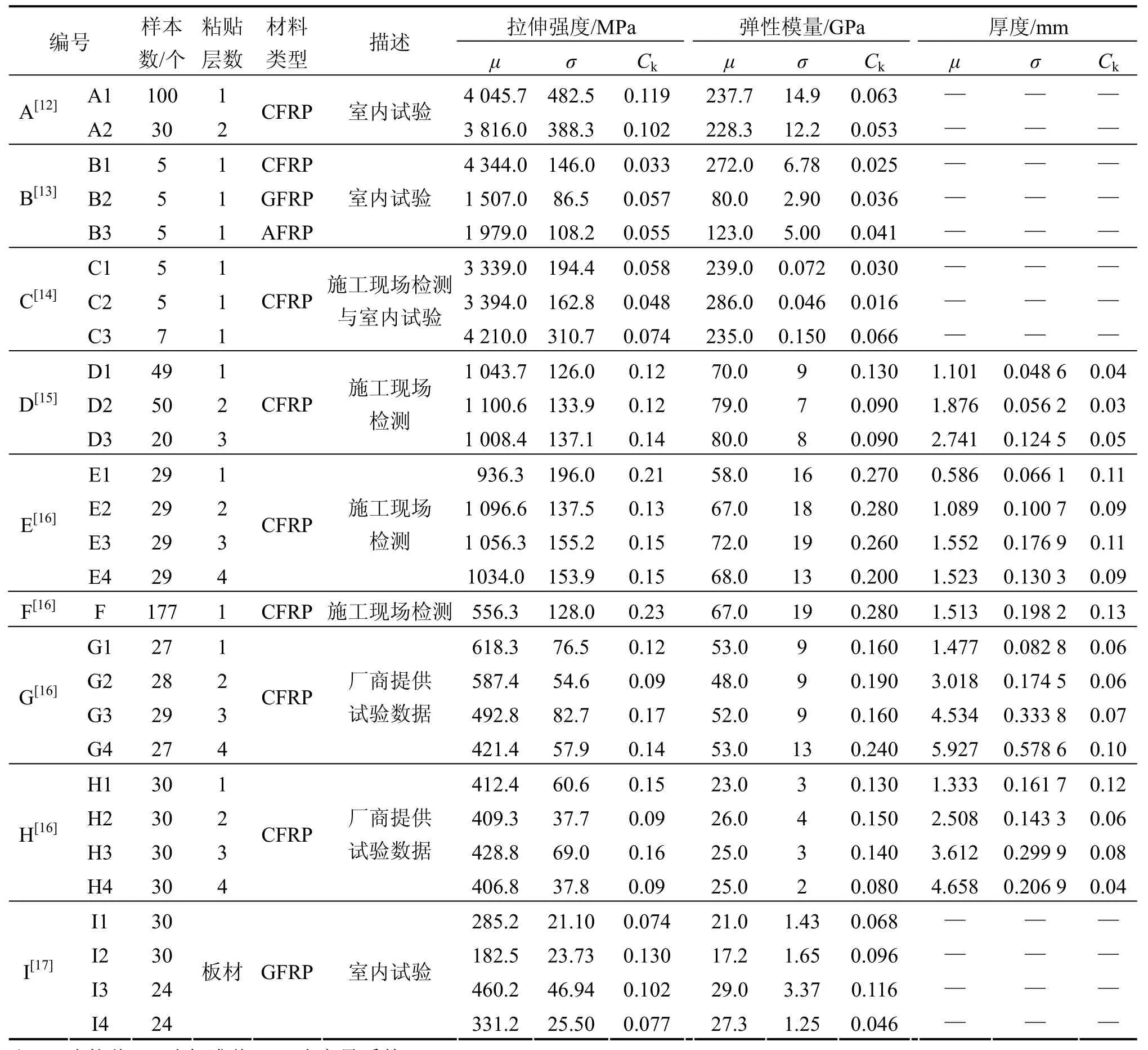
表1 FRP材料力学性能试验样本与参数统计Table 1 FRP data sets and descriptive statistics for mechanical property

图1 A1和D1组极限抗拉强度累积概率分布图Fig.1 Plot of CDF for set A1 and D1 tensile strength

3 参数分布类型拟合优度检验

本文采用 3种拟合优度检验方法，χ2检验(Chi-Square)、K-S检验(Kolmogorov-Smirnov)和 A-D检验(Anderson-Darling)对试验样本进行统计分析。由于不同分布类型对不同检验方法的接受标准不同，为了对比不同分布类型的拟合程度，以在同一显著性水平α检验数组接受或拒绝检验的程度来衡量分布类型的拟合程度，χ2检验和K-S检验采用显著性水平α=0.1进行检验；A-D检验采用α=0.25进行检验。

3.1 极限抗拉强度指标检验

由χ2检验结果如表2所示。由表2可知：各数组对4种分布类型均可接受检验，但从测试参数χq2看，数值越小表示分布类型接受检验的程度越高。表2中黑体为该数组的最优分布类型，可见各组的最优分布类型一致性不强，这主要是由于χ2检验将数值进行分组，容易导致差异较大值被忽略，而使假设通过检验。但从总体上看 Weibull分布较其他分布更具适用性。K-S检验与A-D检验结果也列于表2。由表2可知：Weibull分布在显著性水平下检验接受程度高于其他类型分布。虽然 Weibull分布并非完全适用于所有数组，但与其他分布类型相比，Weibull分布的拟合效果最好，且在航空、航天工业中纤维复合材也已广泛采用Weibull概率分布。因此，选取Weibull分布为材料极限抗拉强度的概率分布类型。

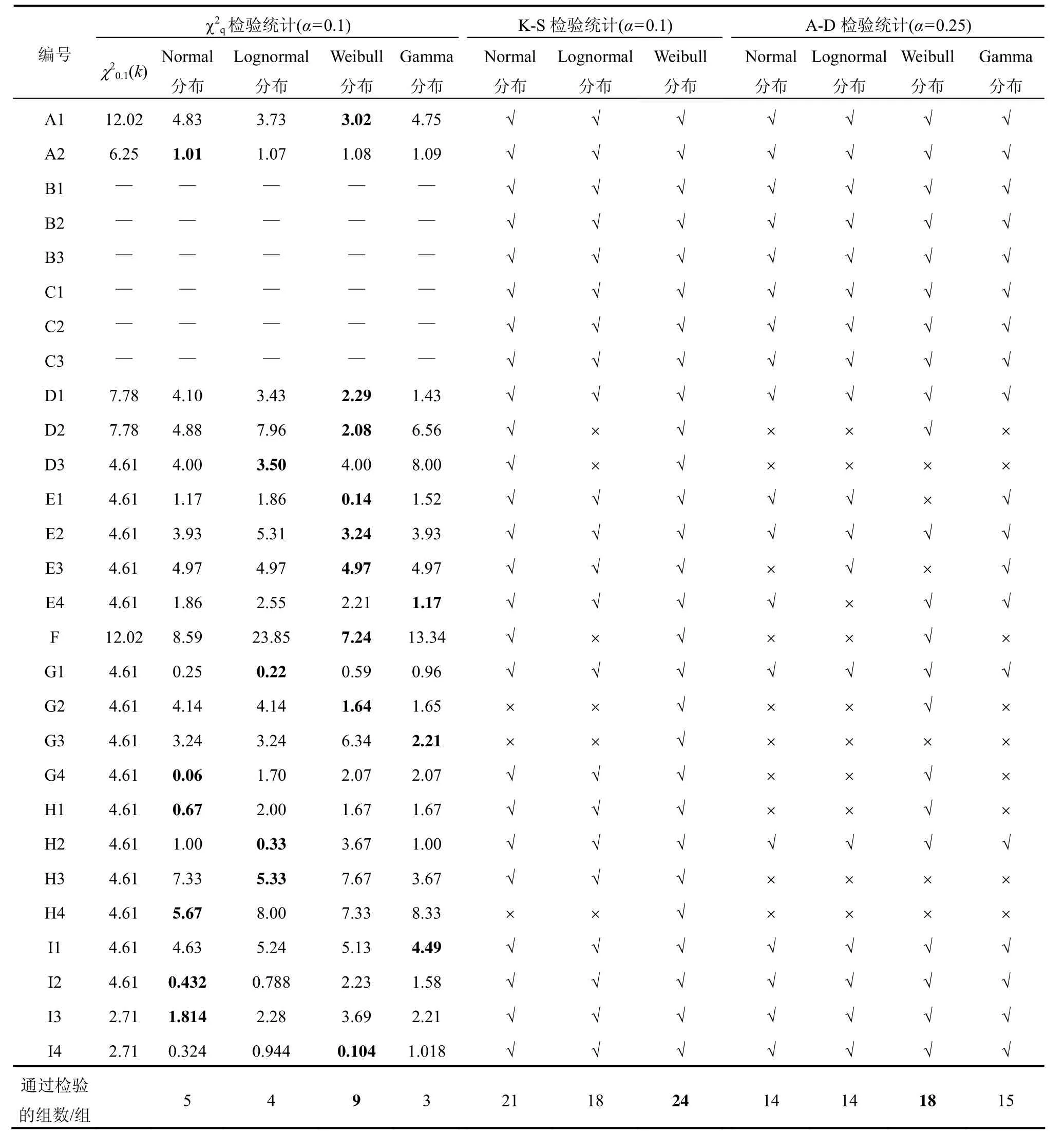
表2 极限抗拉强度拟合优度检验结果Table 2 Goodness of fit test result for tensile strength

3.2 弹性模量指标检验

χ2检验结果表明：Weibull分布与Lognormal分布对弹性模量参数的拟合程度较好；K-S检验表明：Weibull分布的接受程度较Lognormal分布高；而A-D检验表明：Weibull分布与Gamma分布较优。因此综合3种检验方法结果，建议选取Weibull分布为材料弹性模量的概率分布类型。

3.3 厚度指标检验

χ2检验、K-S检验及A-D检验对材料厚度检验结果均表明：Lognormal分布的接受程度优于其他分布类型，因此选取Lognormal分布为材料厚度的概率分布类型。

3.4 参数相关性分析

已有研究[2]中均视材料参数为相互独立变量，然而若各参数间存在相关性，则会对可靠度分析产生影响。以ρ表示各参数之间的相关程度，当|ρ|＜0.2时，视各参数间不相关；当|ρ|＞0.8时，视各参数间完全相关。经参数相关性分析可知：极限抗拉强度、弹性模量和厚度3个参数间呈现一定的弱相关性，相关系数在不同数组间变异性较大。极限抗拉强度与厚度、弹性模量与厚度呈负相关性，这是由于材料强度、弹模与应力相对应，厚度减小，材料横截面积减小，在恒定拉力作用下，应力增大。因此，高强度、高弹模与较薄厚度相对应。同时，负相关性与厂商也有一定关系，越薄的材料代表制造水平越高，材料性能越好。

4 基于Weibull分布的强度标准值

4.1 已有FRP强度标准值

材料强度标准值的选取是进行设计分析的基础，一般要求对至少20个样本统计分析，并考虑环境、工艺、测试方法等因素，取概率分布某一分位值计算确定强度标准值，其计算表达式如下：

式中：xk为强度标准值；μk为样本均值；σk为样本标准差；n为常数。不同规范对常数n有不同。由于Weibull分布更合适描述拉伸强度指标，因此本文重新定义拉伸强度标准值。

4.2 标准值定义

Weibull概率密度函数中尺度参数η、形状参数β与样本均值μ和变异系数Ck有关。

采用式(7)和(8)计算参数η和β时，未考虑样本数量限制而使参数η和β产生统计不确定性。因此本文采用最大似然数估计方法，对服从Weibul概率分布的η和β进行估计。假设样本个数为n，其中x1，x2，…，xn是Weibull概率分布的观察值，Weibull分布中参数η和β未知，Weibull分布似然函数为：

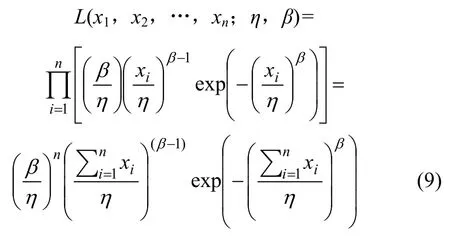
根据式(9)，采用Matlab编程计算参数η，β的估计量。由η，β估计量，根据分位值p确定拉伸强度标准值，本文按照可靠度统一理论取p=5%分位值，即P[X＜xp]=p，拉伸强度标准值xp为：

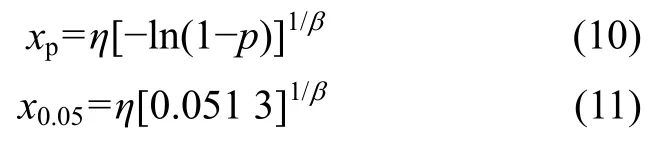
4.3 材料标准值计算与对比分析

根据上述推导分析，现以 A1数组为例计算拉伸强度标准值，已知A1组试样个数n＝100；β=10.81；η=4 121；假设置信水平r＝0.95；p为5%分位值，则由此可得：x0.05为3.131 GPa。

将计算得到各组样本的等效 Weibull分布拉伸强度标准值与3个规范[18-20]的规范值进行对比，结果如表 3所示，其中，Pd为标准值与规范值的对比度，Pd=[(xp-xk)/xk]×100%。由表3可知，在相同分位值下，等效 Weibull分布材料标准值较各规范建议值偏于安全。由于规范建议值并非基于验证的概率分布，且系数的选取基本是以混凝土或钢筋的统计分析为基础，因此采用经验证的 Weibull分布及得到的标准值较规范取值具有较高的可靠性及适用性，同时也可为进一步研究基于可靠度的FRP加固混凝土结构设计方法提供一定理论依据。

表3 等效Weibull分布拉伸强度标准值与规范值对比Table 3 Comparision of equivalent weibull characteristic values to current guideline characteristic values

5 结论

(1) 材料极限抗拉强度与弹性模量近似服从二参数Weibull分布；厚度近似服从对数正态分布。

(2) 3个指标间呈现一定的弱相关性，相关系数在不同数组间变异性较大。极限抗拉强度与厚度、弹性模量与厚度呈负相关性。

(3) 通过相同分位值下等效 Weibull分布拉伸强度标准值与现行规范取值的对比分析可知，现行规范对FRP拉伸强度标准值取值差异较大，而采用经验证的Weibull分布函数计算公式可较好估计材性标准值，计算结果较规范取值更为合理、安全。

[1]Alqam M,Bennett R M,Zureick A H. Three-parameter vs.two–parameter Weibull distribution for pultruded composite material properties[J]. Composite Structures,2002,58: 497-503.

[2]Pevris N,Triantafillou T C,Veneziano A. Reliability of RC members strengthened with CFRP laminates[J]. Journal of Structural Engineering,1995,121(7): 1037-1044.

[3]Okeil A M,Tawil E L,Shahawy M. Flexural reliability of reinforced concrete bridge girders strengthened with carbon fiber-reinforced polymer laminates[J]. Journal of Bridge Engineering,2002,7(5): 290-299.

[4]Neocleous K,Pilakoutas K,Waldron P. Structural reliability for fiber reinforced polymer reinforced concrete structures[C]//Proceedings of the International Symposium on Fiber Reinforced Polymer Reinforced for Reinforced Concrete Structures(FRPRCS-4). Baltimore,Maryland,Detroit: American Concrete Institute,1999: 65-74.

[5]Pham H B,Al-Mahaidi R. Reliability analysis of bridge beams retrofitted with fibre reinforced polymers[J]. Composite Structures,2008,82: 177-184.

[6]Atadero R,Lee L,Karbhari V M. Consideration of material variability in reliability analysis of FRP strengthened bridge decks[J]. Composite Structures,2005,70: 430-443.

[7]Pliakoutas K,Neocleous K,Guaandagnini M. Design philosophy issue of fiber reinforced polymer reinforced concrete[J]. Journal of Composites for Construction,2002,6(3): 154-161.

[8]何政,李光. 基于可靠度的FRP筋材料分项系数的确定[J].工程力学,2008,25(9): 214-221.HE Zheng,LI Guang. Reliability-based calibration of material partial factor of fiber reinforced polymer rod[J]. Engineering Mechanics,2008,25(9): 214-221.

[9]杨勇新. 碳纤维布加固混凝土梁的可靠度分析[J]. 建筑结构学报,2008(S1): 88-92.YANG Yong-xin. Reliability analysis of RC concrete beams strengthened with CFRP sheets[J]. Journal of Building Structures,2008(S1): 88-92.

[10]李业绩,岳清瑞,杨勇新,等. 加固修复用碳纤维布力学性能试验值的研究[J]. 玻璃钢/复合材料,2008,25(9): 9-12.LI Ye-ji,YUE Qing-rui,YANG Yong-xin,et al. Stduy on mechanical property testing values of carbon fiber sheets uesd in strengthening and rehabilitation[J]. FRP/CM,2008,25(9): 9-12.

[11]于明伟. 单一纤维FRP筋基本力学性能与混杂FRP筋的研制[D]. 哈尔滨: 哈尔滨工业大学土木工程学院,2005: 35-42.YU Ming-wei. Mechanics properties study on FRP rebars and development of hybrid FRP rebars[D]. Harbin: Harbin Institute of Technology. School of Civil Engineering,2005: 35-42.

[12]岳清瑞,曹劲松,杨勇新,等. 碳纤维布标准检测方法中试件尺寸影响的试验研究[J]. 工业建筑,2005,35(8): 1-4.YUE Qing-rui,CAO Jin-song,YANG Yong-xin,et al. Normative specimen of carbon fiber reinforced polymer sheets for checking property[J]. Industrial Construction,2005,35(8): 1-4.

[13]孙秀红,徐向东,徐茂波. 影响 FRP基本力学性能的因素[J].山东建筑工程学院学报,2005,20(2): 18-23.SUN Xiu-hong,XU Xiang-dong,XU Mao-bo. Factors to influence fundamental mechanical behaviors of FRP[J]. Journal of Shandong University of Architecture and Engineering,2005,20(2): 18-23.

[14]朱红,张继文. 结构加固过程中 CFRP布基本力学性能的检测[C]//第二届全国土木工程用纤维增强复合材料(FRP)应用技术学术交流会论文集. 昆明: 2002: 324-329.ZHU Hong,ZHANG Ji-wen. Test on the main mechanical properties of FRP[C]//The 2nd National Conference on FRP Concrete Structures. Kunming,2002: 324-329.

[15]Lee L S. Monitoring and service life estimation of reinforced concrete bridge decks rehabilitated with externally bonded carbon fiber reinforced polymer (CFRP) composites[D]. San Doego: University of California. Department of Structural Engineering,2005: 126-128.

[16]Atadero R A,Karbhari V M. Source of uncertainty and design value for field-manufactured FRP[J]. Composite Structure,2009,89(5): 83-93.

[17]Zureick A,Scott D. Short-team behavior and design of fiber-reinforced polymer slender members under axial compression[J]. Journal of Composite for Construction,1997,2(1): 140-150.

[18]ACI440.12R－02. Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures[S].

[19]TR-55. Design guidance for strengthening concrete structures using fiber composite materials[S].

[20]GB 50367—2006,混凝土结构加固设计规范[S].GB 50367—2006,Design code for strengthening concrete structure[S].