无向通信网端对端可靠性通用算法

刘京和

(总参信息化部军事代表局,北京100840)

0 引言

通信网可靠性分析是目前被广泛研究的课题之一。在种种不同的网络可靠性问题中,端对端可靠性是研究得最多的课题。在该问题中,往往是给出具有2个规定节点(源和汇)的网络G以及节点和链路的故障概率,求源和汇之间至少有一条通路的概率。

无向网络端对端可靠性与有向网不同,具有不可靠节点的有向网能够比较容易地转化成具有完全可靠节点的有向网,而无向网目前还不能进行上述转化,因此端对端可靠性算法对有向网是通用的,而对无向网却不能通用。目前,大量文献研究解决的是假定节点完全可靠、链路不可靠情况下无向网络端对端可靠度分析算法。该文提出了一种无向网络中通用的可靠性算法,无论节点和链路可靠与否,都可直接进行分析和计算。

1 分解定理

为了对无向网进行简化和分解,首先对几个关键的定理进行推导。定理中的参数表示如下。

G(V,E)：网络 G,其中 V为节点,E为链路;

G-x：从网络G中删去x后的网络;

G*x：从网络G中吸收掉x后的网络;

s：网络的源节点;

t：网络的目标(汇)节点;

vi：网络中的第 i个节点;

ei,j：网络中节点vi和vj之间的链路;

{ei,j}：与节点 vi连接的链路集;

pi,qi：网络中节点vi可靠、故障的概率;

pi,j,qi,j：网络中链路 ei,j可靠、故障的概率;

R(G)：不包括节点vs和vt的端对端s-t可靠度;

Rs-t(G,pv,pe)：G的端对端 s-t可靠度,即Rs-t(G,pv,pe)=R(G)◦ps◦pt。

定义网络G为单调关联系统,有结构函数 φ,φ∈{CS}。

定理1 设 φ∈{CS},则对任意的 i∈N和 x,有：

上式称为 φ的分解公式。

证明：因为

上式右端即定理1中公式右端。

定理2 网络G可靠度分解公式

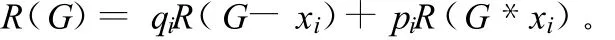
其中 G-x为从网络G中删去x后的网络,G*x为从网络G中吸收掉x后的网络。

证明：由定理1分解公式

φ(x)=xiφ(1i,x)+(1-xi)φ(0i,x),再由网络部件独立性即得证。

定理3 设网络G中存在一条s-t通路

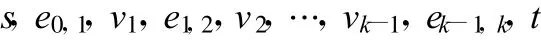
s-t通路的链路是 ei-1,i,0≤i≤k,节点是vi,1≤i≤k-1。

式中,R(G*e0,1*v1*e1,2*v2*…*vk-1*ek-1,k)=1,最后该条s-t通路收缩成一条完全可靠的链路。

证明：如果G中不存在s-t通路,Rs-t(G)=0。如果有s-t通路,可以对链路e0,1进行分解。因此：

在G*e0,1中,节点s和v1视为用概率为1的链路连接,同时把节点v1与其相连接的链路都删去,有

类似地,对k条链路和k-1个节点应用分解定理2k-1次,有定理3。

2 分解算法与流程

2.1 分解算法

为求具有长度为2k-1的s-t通路网络可靠度R(G),把网络G分解成2k-1个子网络,一直分解下去,最终可递归解出R(G)。可见,至少有一条s-t通路的每个子网络要比原先网络简单。

在式(1)中,若网络G的节点完全可靠,式(1)可以被简化为：

同样,若网络G的链路完全可靠,式(1)可以被简化为：

最终可得网络G规定节点对s-t之间的可靠度为：

2.2 分解流程

根据式(1),无向网络G化简分解算法简述如下：

①寻找G中最短的一条s-t通路,令x=1;

②去掉第x个部件,得到子图G-x。把子图及相关数据pi放入堆栈中;

③如果可利用化简规则的话,进行deg(v)=1和deg(v)=2化简;

④如果G-x仍有s-t通路,回到第1步,否则从堆栈中取出相应数据计算R;

⑤从堆栈中取出子图G,令x=x+1,如果x≤2k-1,回到第2步,如果 x=2k结束。

其流程图如图1所示。

每个网络在找s-t通路之前,都先进行化简。这样才能有效地减低子网络的复杂程度。对每个子网络反复利用上述算法,递归解出它们,然后再将其合并就是最终的结果。由于具有失效概率为q的单元部件(链路和/或节点)的数量每步至少减少1个,每次递归中,循环深度由网络单元部件数量决定,递归算法需要内存为O(#节点数2◦#单元部件数)。可见,对每个子网络寻找一条最短的s-t通路是使算法最优的重要条件之一。

图1 网络端到端可靠性计算的简化流程图

3 端到端可靠度计算

把该算法表述为一个函数UNRP。子程序PATH(G,found,path,length)是寻找一条s-t通路,对dijkstra或floyd算法略加修改即可。假定G中至少存在一条s-t通路的话,置变量found为真,并利用变量length返回该通路的长度。该通路上的单元部件序列用一维数组变量path(i)返回。计算程序所需的输入数据用一个加权邻接矩阵表示,二维数组变量为 entry(i,j)。i≠j时,代表从节点vi到vj链路的可靠度;i=j时,代表节点 vi的可靠度。网络化简在计算机的端对端可靠度过程中,对减少网络状态数和占机CPU运行时间起着重要的作用。

Wood讨论了计算机网络可靠度的化简方法[2]。对无向网络端对端可靠度的计算,常用的化简方法有节点degree-1,degree-2及并联化简。化简必须保证不改变网络的可靠度为原则。

令网络G(V,E)化简后的网络为G'(V',E'),对应的可靠度有如下的关系：

式中,C0是化简常数。

对无向网络端对端可靠度计算中化简规则给出如下。

3.1 Degree-1化简

令Let deg(vi)=1,vi∈V

情形1：i=s或j=t。网络G中有链路ei,j和节点vi(或 vj),ei,j∈E,vi(vj)∈V。那么,吸收掉 ei,j和vi(或 vj)获得网络 G'。对于 j=t,C0=pi,jpj,V'=V-vj,E'=E-ei,j,对于 i=s,C0=pipi,j,V'=V-vi,E'=E-ei,j。

情形2：i≠s(或 t)。网络 G中有链路,ei,j,和节点,vi(或vj),ei,j∈E,vi(vj)∈V。那么,删去 ei,j和vi(或vj)获得网络 G'。C0=1,V'=V-vi,E'=E-ei,j。

3.2 Degree-2化简

情形1：网络G中的链路完全可靠时,设在节点va和vb之间存在2个串联节点vi和vj,deg(vi)=deg(vj)=2,ea,i,ei,j,ej,b∈E,vi,vj∈V。那么,用一个新的节点vc代替vi,ei,j和vj,得到网络G'。C0=1,pc=pi,jpj,V'=V-vi-vj+vc,E'=E-ei,j。

情形2：其他。设网络G中有两条串联的链路ei,j和ej,k,其中 deg(vj)=2,ei,j,ej,k∈ E,vj∈ V。那么,用一条新的链路ei,k代替ei,j,vj和ej,k,得到网络G'。C0=1,pi,k=pi,jpjpj,k,V'=V-vj,E'=E-ei,j-ej,k+ei,k。

3.3 并联化简

4 算法分析

图2给出了3个有代表性的无向网络[1]。

图2 3种代表性的无向网络

图2分别为最简网络 G1、中等复杂网络 G2和较大复杂网络G3。如表1所示,对应以下3种情况计算网络G1、G2、G3的可靠度：网络中节点完全可靠,链路不可靠;链路完全可靠、节点不可靠;以及节点和链路均不可靠。网络部件故障率分别为10%、20%和30%。表2摘录了文献报道的算法、语言、运算时间开销与该文相应结果的比较。

表1 网络可靠性计算结果

表2 无向网络端对端s-t的算法的比较

通过对算法的分析,表1给出网络可靠性计算结果。不难看出,该文中的算法优于参考文献中的算法。

5 结束语

针对无向网络端对端可靠性算法不通用的特点,对传统可靠性算法进行优化,无论节点和链路可靠与否,都可直接进行分析和计算。该算法大大降低计算的复杂度,在无向网络端对端可靠性的分析和计算中,简化了计算流程,大大减少计算时间,适用性好,可作为无向网络端对端可靠性分析的通用算法。

[1]KALIMULINA E Y.A parallel Algorithm forReliability Optimization of Communications Systems[C]∥SIBCON(Siberian Conference on Control and Communications),2009：22-24.

[2]WOOD R K.Factoring algorithm for computing K-terminal network reliability[J].IEEE Trans.Reliability,1986,35：269-278.

[3]BUZACOTT J A.A recursive algorithm for finding reliability related to The connection of nodes in graph[J].Network,1980,10：38-43.

[4]PROVAN J S,BALL M O.Computing network reliability in time polynomial in the number of cuts[J].Operations Research,1984,32：65-70.

[5]BAILEY M P,KULKAMI V G.A recursive algorithm for computing exactreliabilitymeasures[J].IEEE Trans.Reliability,1986,35：36-40.

[6]PAGE L B,PERRY J E.A practical implementation of the factoring theorem for network reliability[J].IEEE Trans.Reliability,1988,37：259-267.