最小偏差法在机械多目标优化设计中的应用
2011-07-31魏锋涛
魏锋涛, 宋 俐, 李 言
最小偏差法在机械多目标优化设计中的应用
魏锋涛, 宋 俐, 李 言
(西安理工大学机械与精密仪器工程学院,陕西西安 710048)
提出了处理多目标问题的最小偏差法,并将其应用于机械多目标优化设计。以流体动压滑动轴承多目标优化设计为例,建立了以摩擦系数最小、发热量最小和承载能力最大为目标函数的多目标优化设计数学模型,根据最小偏差法原理构造统一目标函数,利用改进遗传算法对该问题进行了优化设计。算例整个求解过程和结果表明,该方法既可以避免人为因素的影响,又能够获得比常规设计更佳的设计参数,同时也验证了所提方法对于解决机械多目标优化设计问题的有效性和可行性。
最小偏差法;机械多目标;优化设计;改进遗传算法
工程中常常会遇到期望一个设计方案的多项设计指标同时都达到最优的多目标优化设计问题,一般在求解多目标优化设计问题时需要作适当处理,构造一个新的函数,即评价函数,将多目标优化设计问题转变成单目标优化设计问题进行求解,最常用的处理方法有主要目标法、线性加权和法、理想点法、平方和加权法、乘除法、功效系数法等。由于多目标优化设计分目标间的矛盾性和不可公度性增加了解决问题的难度,使得对多目标优化设计不能建立一个纯客观的选优判据。多目标优化设计的困难之处在于建立一个反映决策者偏好的选优衡准,即各目标函数的重要性排序。若目标函数或权数选择不同,则得到的优化结果也不同,决策结果往往带有一定程度的相对性和主观性,不能真实地反映客观事实。为此,本文引入统一目标函数最小偏差法,该方法仅需要分析者和决策者的局部信息,即各个目标函数的最优解,而无需知道它们的相对重要性,避免了权系数的选择,使优化设计结果更加客观实际。
本文提出将无量纲的最小偏差法应用于流体动压滑动轴承的多目标优化设计,以流体动压径向滑动轴承的摩擦系数最小、发热量最小和承载能力最大为目标函数建立多目标优化设计数学模型,根据最小偏差法原理构造统一目标函数,利用改进遗传算法对该多目标优化问题进行了优化设计。算例结果表明,最小偏差法应用于解决机械多目标优化设计问题是有效的、可行的。
1 最小偏差法
一般多目标优化设计问题数学模型可以描述为

从式(1)可以看出,多目标优化问题是一个向量函数的优化,即函数值大小的比较,而向量函数值大小的比较,要比单目标优化问题标量函数大小的比较复杂的多。因此,在多目标优化过程中,往往要比较这些向量函数的“大小”,为此需要引入一个“有效解”,即Pareto最优解的概念,它是于1951年由T C Koopmans正式提出的。
对于多目标优化问题,设法求解的既是问题的有效解(或弱有效解),又是在某种意义上令决策者满意的解。根据多目标优化问题的特点以及决策者的意图,构造一个统一目标函数
(2)
采用不同形式的统一目标函数可求得不同意义的解,并对应于不同的求解方法。此处,采用最小偏差法,取统一目标函数为
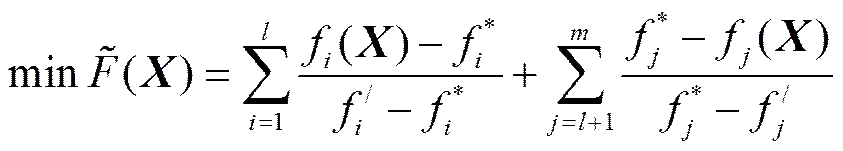
2 流体动压滑动轴承多目标优化设计数学模型
流体动压径向滑动轴承具有承载能力大、功耗小、耐冲击、抗振性好、运转精度高等突出的优点。所以,在高速低速以及高速精密的旋转机械中应用十分普遍,而且成为旋转机械的重要部件。对流体动压滑动轴承按常规方法设计,轴承的宽径比、轴承孔和轴颈的相对间隙等参数的确定都是按经验在一个取值范围内选取的,因此带来了耗油量大、温升高且承载能力小等问题。为了提高流体动压滑动轴承的综合性能,对流体动压滑动轴承进行多目标优化设计,获取更加合理的结构参数很有必要的。
2.1 设计变量
设计滑动轴承时,要根据实际情况,选用对滑动轴承性能影响较大的结构参数作为设计变量。影响滑动轴承工作性能的主要参数有:宽径比,相对间隙,润滑油动力粘度。故设计变量可选择为

2.2 目标函数
根据流体动压滑动轴承的工作特点,应以获得最佳承载能力与工作状态作为目标函数,本文将摩擦系数最小、发热量最小和承载能力最大为目标函数作为流体动压滑动轴承多目标优化设计的目标函数。
(1)摩擦系数最小
为使滑动轴承传动效率最大,应使其摩擦阻力,即摩擦系数最小,故此目标函数为

(4)
(2)发热量最小

(3)承载能力最大
在流体动压滑动轴承的设计中,首先要保证轴承具有足够的承载能力,而体现轴承承载能力的一个重要参数是承载量系数,若越大,则轴承的承载能力也越大。故选择承载能力最大为优化设计的目标函数之一,即
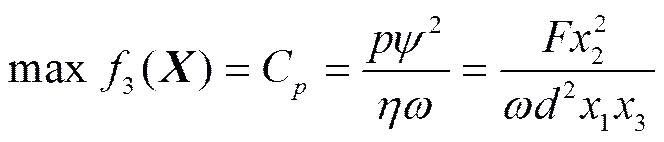
2.3 约束条件
(1)最小油膜厚度

(2)轴承宽径比
轴承设计规范一般要求
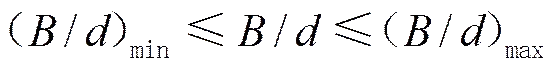
(8)
(9)
(3)比压

(11)
(4)轴承相对间隙

(13)
(5)润滑油粘度

(15)
2.4 数学模型
综上所述,流体动压滑动轴承多目标优化设计的数学模型表示为

用最小偏差法取统一目标函数为
(17)
3 流体动压滑动轴承多目标优化设计实例
设计一矿井提升机的流体动压润滑径向滑动轴承,已知工作载荷,载荷平稳,轴颈直径,轴的转速,瓦衬材料为巴氏合金,轴承为剖分式。对于该提升机的动压润滑径向滑动轴承,可取,,,,,。
对标准遗传算法进行了实数编码策略、联赛选择机制及动态调整交叉概率和变异概率引入自适应算子等方面的改进,参数设置为:群体规模,,,,,采用终止代数为200代与优化判据相结合的方法来判断是否结束程序的运行,并以连续10代平均目标函数值不大于最小目标函数值0.001作为优化判据,并将改进后的遗传算法应用于求解该多目标优化设计问题,优化设计结果与常规设计结果对比如表1所示。

表1 优化设计与常规设计结果对比表
从表1可以看到,用利用最小偏差法进行优化设计,可使摩擦因数减小、发热量降低、承载能力显著提高,其中,摩擦因数减小了12.5%,发热量降低了16.9%,承载能力提高了68.3%,可以得到比常规设计更为合理的设计方案。
4 结 论
本文根据最小偏差法原理,建立了流体动压径向滑动轴承多目标优化设计的统一目标函数,采用改进遗传算法对该问题进行了求解。整个求解过程和优化设计结果表明,最小偏差法克服了常规设计方法在参数取值时所带有的一定的盲目性,避免人为因素的影响,能够获得比常规设计更佳的设计参数,充分显示了该方法的有效性及可靠性,是一种更有效的多目标优化设计方法,对于解决机械多目标优化设计问题具有一定的实用价值。
[1] 孙靖民. 机械优化设计(第3版)[M]. 北京: 机械工业出版社, 2003. 176-191.
[2] 濮良贵, 纪名刚. 机械设计(第8版)[M]. 北京: 高等教育出版社, 2006. 286-299.
[3] AKIHIKO ABE. Optimization of construction of tire reinforcememt by genetic algorithm [J]. Optimization and Engineering, 2004, (5): 77-92.
[4] Bishop J A, Striz A G. On using genetic algorithms for optimum damper placement in space trusses [J]. Structural and Multidisciplinary Optimization, 2004, (9): 136-145.
[5] 林 丹, 李敏强. 基于遗传算法求解约束优化问题的一种算法[J]. 软件学报, 2001, 12(4): 628-632.
[6] 吕 波, 吴鹿鸣. 遗传算法与惩罚函数法相结合在约束优化问题中的应用[J]. 机械科学与技术, 1999, 18 (5): 732-734.
[7] 邱宣怀, 郭可谦. 机械设计[M]. 北京: 高等教育出版社, 1997. 335-352.
Application of Minimum-Deviation Method to Mechanical Multi-objective Optimal Design
WEI Feng-tao, SONG Li, LI Yan
( School of Mechanical and Instrumental Engineering,Xi’an University of Technology , Xi’an Shaanxi 710048, China )
The minimum-deviation method is introduced into the mechanical multi-objective optimal design. Taking a multi-objective optimal design of hydrodynamic sliding bearing as the example and taking the minimization of friction coefficient and heat productivity,and the maximization of load capability as objectives, the minimum-deviation method is adopted to establish the multi-objective optimal mathematical model. The improved genetic algorithm is utilized to solve this multi-objective optimal problem. The solution-seeking process and its results show that the minimum-deviation method can obtain better results than conventional methods in dealing with multi-objective optimal problem and the validity and feasibility of the method is verified.
minimum-deviation method; mechanical multi-objective; optimal design; improved genetic algorithm
TH 132.44
A
1003-0158(2011)03-0100-05
2010-04-21
陕西省重点学科建设专项资金资助项目(102-00X903);西安理工大学科学研究基金资助项目(102-210913)
魏锋涛(1976-),男,陕西合阳人,讲师,博士研究生,主要研究方向为多目标多学科优化设计。
