一种参数三次样条曲线光顺优化算法
2011-07-31章虎冬
章虎冬
一种参数三次样条曲线光顺优化算法
章虎冬
(西安邮电学院应用数理系,陕西西安710121)
论文给出了一种基于修改因子和修改角度的平面参数三次样条曲线的优化光顺算法,该算法通过求解一个带有修改因子和修改角度的目标函数得到光顺后的型值点,插值光顺后的型值点得到光顺曲线。目的是使曲线的曲率变化均匀的同时,使光顺后的曲线与原曲线的偏差尽量小,此算法简单易行,计算量较小。
计算机应用;自动光顺算法;修改因子;修改角度;参数三次样条曲线
计算机辅助几何设计中的一项重要任务就是如何根据给定的数据点产生一条光顺的曲线或曲面。但是,由于数字化过程中的误差影响,一般得到的插值或拟合曲线(或曲面)不能令人满意,这样,对曲线或曲面进行光顺,就显得至关重要。就曲线而言,光顺法可以分为优化法和选点修改法;其中Kjellander采用了Hermit插值来调整型值点;基本思路是:运用近似的作为参数三次样条曲线的能量,然后插值“坏点”两边的点和切矢生成三次Hermit曲线,用“更好”的点来代替“坏点”,然后生成光顺曲线;但是,这种光顺法也有偶然失败的时候,例如美国波音公司的李(Lee,1989)就给出了反例。Sapidis N,康宝生等采用了节点删除和插入法;满家巨等给出了基于扰动控制顶点的B样条曲线光顺法;它们都属于选点修改法。曲线选点修改法的主要步骤:①找出“坏点”;② 对“坏点”进行修改和插值曲线;③ 反复循环以上两步,直至插值出较满意的曲线;其缺点是算法每次只能调整一个控制顶点,局部算法可适用于对一些简单曲线进行光顺,对数据量较大的复杂曲线运用局部算法光顺往往需要多次重复对曲线进行调整,不但运算量大,且难以保证曲线的整体效果。本文给出了一种基于修改因子和角度的平面参数三次样条曲线的光顺算法,运用光顺准则来找出需要光顺的“坏点”,然后通过求解一个带约束的优化问题求得调整后的点的位置,通过插值光顺后的点得到光顺曲线。此算法的目的是使曲线的曲率变化均匀的同时,使光顺后的曲线与原曲线的偏差尽量小,此算法简单易行,计算量较小。
1 参数三次样条曲线及其求解


(2)
(3)

(5)
联立式(3),式(4)与式(5),得到下面的方程组
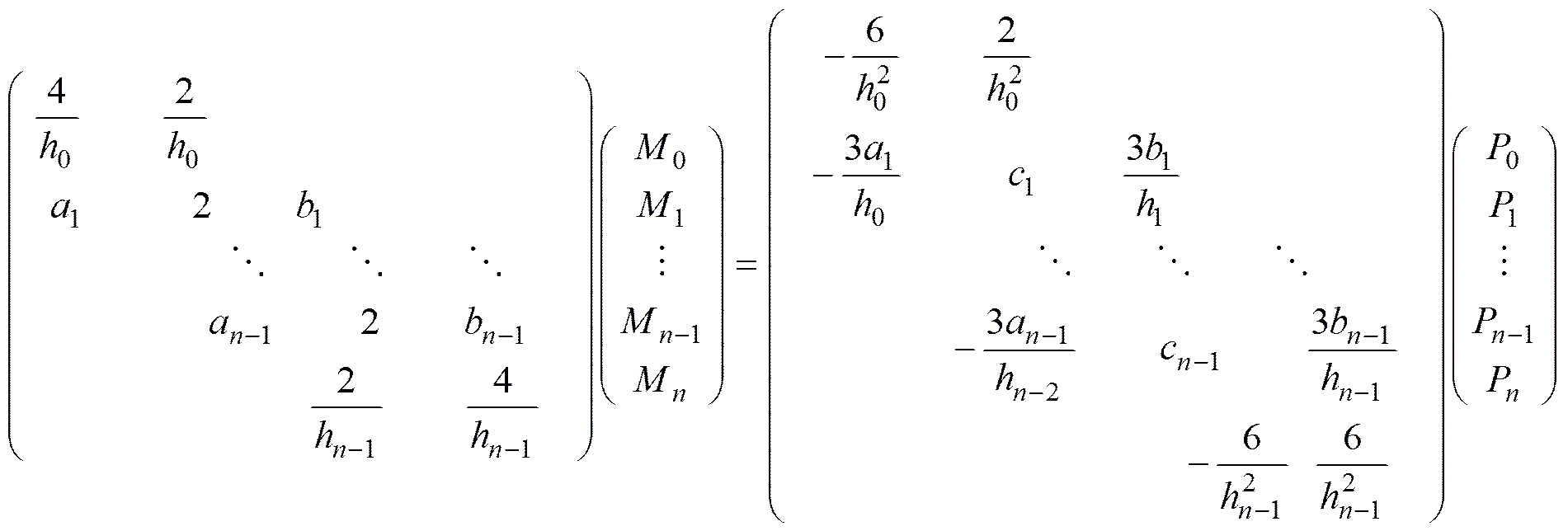
由于最左边的矩阵主对角占优,所以方程组有唯一解,求解式(6),把得到的代入式(2),可求出。
2 ‘坏点’的判别
对曲线进行光顺,首先必须给出具体的光顺准则,目前在光顺中经常使用的光顺准则有:
光顺准则1(Farin等给出):一条曲线是光顺的,如果相应的曲率曲线是连续的,有适当的符号(如果曲线的凹凸性已知),且尽可能地接近一个有着尽可能少的单调段的分段单调函数。
光顺准则2(苏步青、刘鼎元等给出):
(1)二阶参数连续(连续);
(2)没有多余拐点;
(3)曲率变化比较均匀。
光顺准则3(施法中等给出):
(1)二阶几何连续(指位置、切线方向与曲率矢连续,记为);
(2)不存在奇点与多余拐点;
(3)曲率变化比较均匀;
(4)应变能较小。
光顺准则4(Hans Hagen等给出):
以应变能量为最小和扰动为最小的线性组合作为光顺准则,即

光顺准则5(Sapidis N等给出):
在相应于z值最大的内节点处曲线应该被光顺,其中,是曲率弧长的导数。
光顺准则6(kjellander给出):
三阶导数跳跃最大的地方曲线应该被光顺。
光顺准则7(poliakoff等给出):
光顺准则8(Janet F Poliakoff等给出):在最大的内节点处曲线应该被光顺,其中
关于这些关顺准则都有自己适合的用途,有的适用于整体光顺,有的适用于局部光顺,作者这里采用计算量小且用于局部光顺的光顺准则6来找出坏点。
3 算法原理
(1)Kjellander方法
(2)本文方法
Step 1 由光顺准则计算出需要光顺的型值点。

Step 3 下面解一个带约束的优化问题

Step 5 反复上面的过程,直到插值出较满意的曲线。
4 算 例
图1是运用Kjellander法对曲线进行光顺的实际算例,图2是运用本文的光顺法对曲线进行光顺的实际算例,这里取,表示光顺前型值点的横坐标序列,表示光顺前型值点的纵坐标序列,表示光顺后型值点的横坐标序列,表示光顺后型值点的纵坐标序列,和是求解方程式(8)得到的值;由下面的曲率图可以看出,不管是Kjellander法还是本文的方法,曲线的光顺性都得到了改善。从对应的曲线图可以看出,本文的光顺法得到的曲线与原曲线的偏差比Kjellander法得到的曲线与原曲线的偏差小;从下面的曲率图可以看出,本文的光顺法得到的曲线的曲率图比Kjellander法得到的曲线的曲率图更加平滑,总之,与Kjellander法相比,本文的光顺法具有更好的光顺效果。

图2 本文光顺法光顺前后的曲线和曲率图 (蓝的点画线是光顺前的曲线和曲率)
5 结 论
本文给出了参数三次样条曲线的优化光顺算法,它是通过解决一个优化问题得到修改因子和修改角度,从而得到光顺后的曲线,数值实例表明,在光顺后的曲线与原曲线的偏差尽量小的情况下,使得曲线得到较好的光顺。
[1] Kjellander J A P. Smoothing of cubic parametric splines [J]. CAD, 1983, 15(3): 175-179.
[2] Lee E T Y. Energy, fairness, and a counterexample [J]. CAD, 1989, 21(1): 37-40.
[3] Sapidis N, Farin G. Automatic fairing algorithm for B-spline curves [J]. CAD, 1989, 21(2): 121-129.
[4] 康宝生, 赵录刚. 平面三次NURBS曲线的自动光顺算法[J]. 计算机辅助设计与图形学学报, 2002, 14(3): 225-227.
[5] 满家巨, 胡事民,雍俊海, 等. B-样条曲线的节点去除与光顺[J]. 软件学报, 2001, 12(1): 143-147.
An Optimal Fairing Algorithm for Parametric Cubic Spline Curves
ZHANG Hu-dong
( Depatment of Applied Mathematics and Physics, Xi’an Posts and Telecomunications Institute, Xi’an Shaanxi 710121, China )
An optimal fairing algorithm for planar parametric cubic spline curves is proposed based on revising gene and revising angle. Faired point can be obtained by resolving a objective function of containing modifying geneand revising angleand faired curves is obtained by interpolating the faired point. The purpose of this algorithm is to make the change of curvature of faired curves more gradual and its deviation from the initial curves smaller. It is shown that the algorithm is simply facile and needs a smaller calculation.
computer application; optimal fairing algorithm; revising gene; revising angle; parametric cubic spline curves
TP 391
A
1003-0158(2011)03-0041-04
2009-11-10
陕西省教育厅基金资助项目(08JK435;09JK728)
章虎冬(1979-),男,内蒙古呼和浩特人,讲师,硕士研究生,主要研究方向为计算机辅助几何设计。
