基于随机振动分析法的双横臂悬架扭杆优化设计
2011-07-31周水庭黄红武朱位宇
周水庭,黄红武,朱位宇
(1. 厦门理工学院 机械工程系,福建 厦门,361024;
2. 湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082)
车辆出现悬架静挠度过大、前悬架偏软、车架容易撞击限位块和前轮定位角度变化超标等现象,这主要是偏频设计值过低和悬架刚度偏小引起的。对于双横臂悬架系统,韩锐等[1]利用矢量代数法建立了悬架导向杆系运动的数学模型;岳惊涛等[2-4]结合有限张量法更精确计算空间机构的运动状态,并分析了硬点坐标对前轮定位参数的影响;曾迥立[5]提出利用悬架传递杠杆比计算悬架刚度。本文利用虚功原理计算悬架刚度用Adams软件进行仿真验证。考虑到路面输入为随机振动,利用功率谱函数建立相关函数,作为约束条件之一,优化计算扭杆基本尺寸,以增加悬架刚度,减少撞击限位块次数,限制前轮定位角的变化。
1 数学模型的建立及求解
1.1 双横臂扭杆悬架导向机构运动学数学模型
双横臂悬架的导向机构可以看作空间四连杆机构,运用矢量代数,结合有限转动张量法计算得到输入轴转动角度与输出轴转动的角度关系的超越方程[6],从而建立悬架导向杆系运动学关系,并通过几何关系,得到各个硬点的变化函数[3]。双横臂悬架结构示意图见图1。图1中:悬架下横臂AB与转轴1链接,上横臂CD与转轴2链接,E为转向节连接点。定义单位矢量和分别为沿转轴1和转轴2转动的正向;β为上横臂CD以C点为旋转中心绕旋转轴2旋转的角度,旋转后,CD变至CD′;α为下横臂AB以A点为旋转中心绕旋转轴1旋转的角度,旋转后,AB变至AB′;O′为车轮轮心;E点为车轮中心线延长线与虚拟主销连线D′B′的交点。
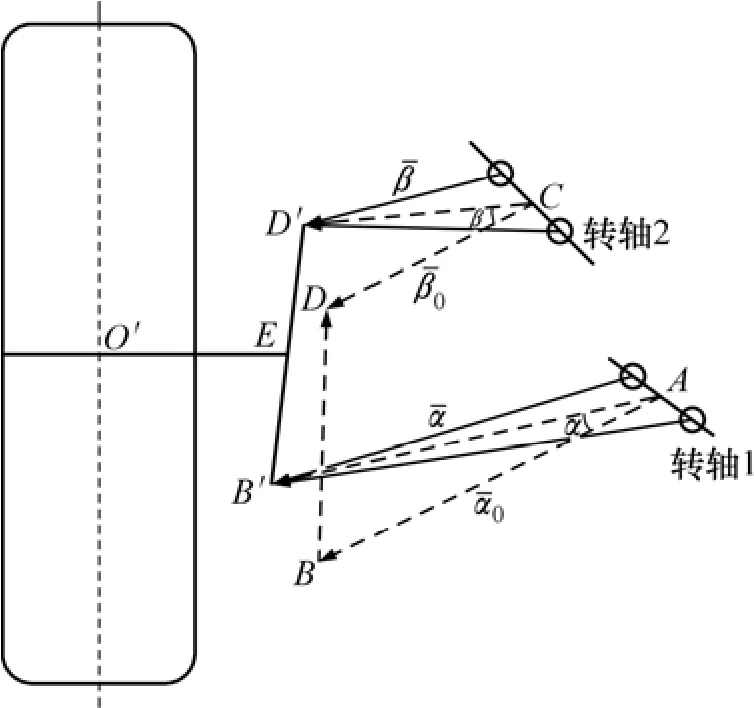
图1 双横臂悬架结构示意图Fig.1 Structural model of torsion bar of double wishbone suspension
1.2 悬架运动过程中的导向机构硬点求解
在上下跳动过程中,由于上外点D只绕转轴2旋转,则根据几何特性,可以求出D点坐标值。根据矢量法,可以得到坐标变化方程[1,3]:
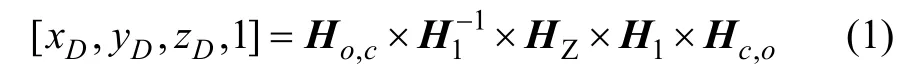
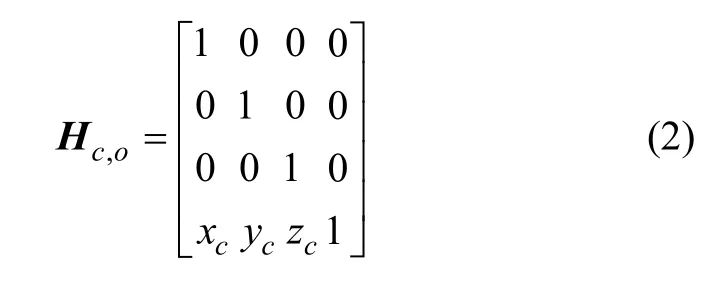
点C坐标系到整车原点O坐标系的位移变换矩阵为:且C坐标系绕O点坐标系Y轴转动角度为-β′O,绕Z轴转动角-α′O,可以求出转动角度变换矩阵为:
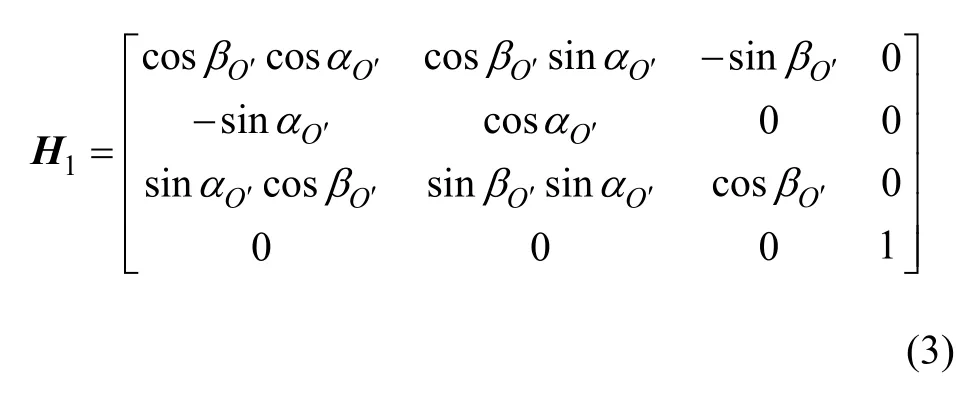
根据上横臂CD绕转轴2旋转角度β,有:
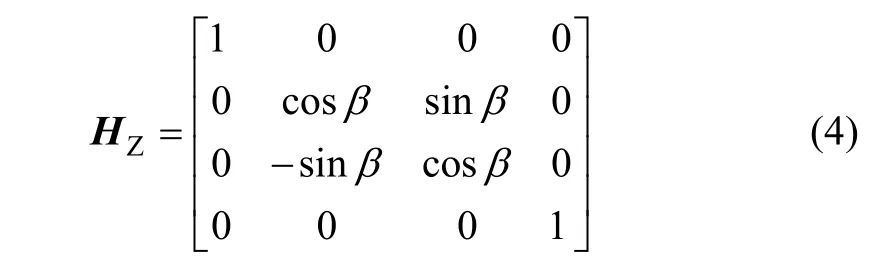
则可以求得外球头点坐标。
在上下跳动过程中,下外点B绕转轴1旋转,可据同样方法求出B点坐标。
根据结构尺寸,轮胎中心至悬架上、下横臂点和转向节中心点的距离不变,根据向量模不变确定位置后,求出O′的位置。轮胎中心O′坐标数学表达式为:
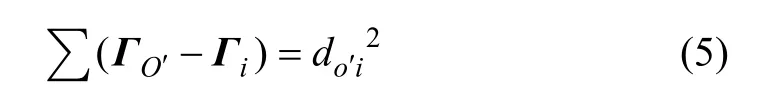
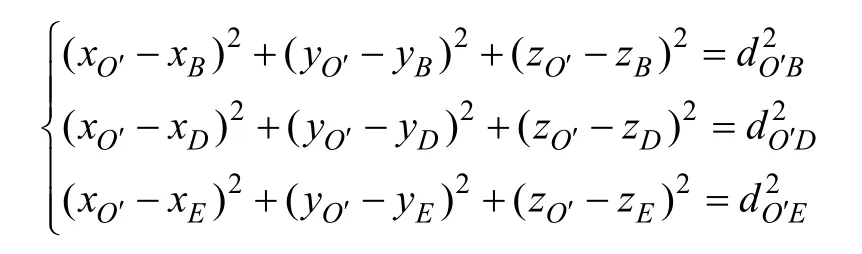
则可以算出轮胎中心O′的坐标;而轮胎中心点处垂向位移变化量可以表示为:
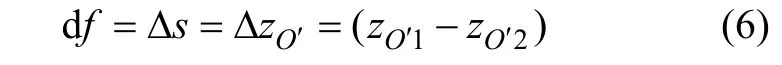
其中:zO′1和zO′2为轮胎中心点z向坐标。
1.3 虚功原理求解悬架刚度
双横臂式独立悬架弹簧的刚度可以假设为垂直作用在车轮上的1个虚拟刚度Cs,P点为上下横臂延长线交点,l为交点P到下横臂B点的距离,m为下横臂长度,dp为交点至轮胎接地处水平距离,Λ为轮距,CT为扭杆刚度,M为扭杆对悬架下横臂的扭矩,如图2所示。
根据虚位移原理[6]可知,在力Fs作用下轮胎绕地面点Q旋转虚角度δφ,下横臂悬架绕点A旋转虚角度δ′,则:
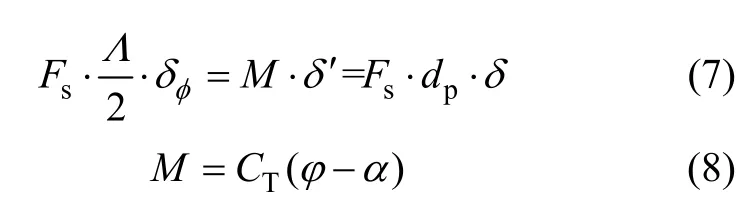
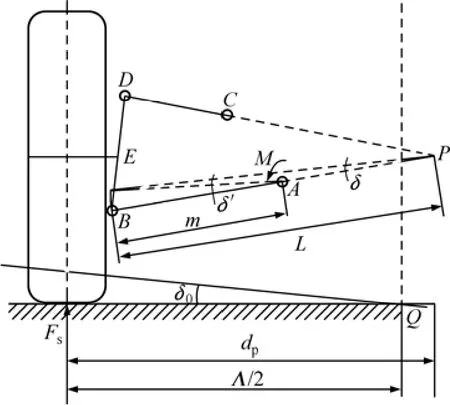
图2 悬架受力示意图Fig.2 Force model of suspension
其中:α为扭杆初始角度;φ为扭杆旋转后角度。
根据几何关系得:

则求得轮胎所受垂向力Fs为:
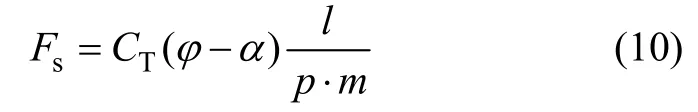
根据刚度定义悬架刚度[7]:
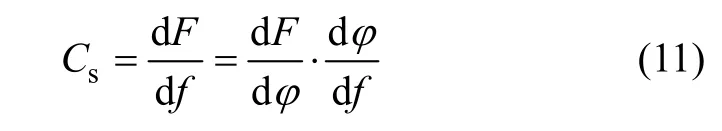
在Matlab中计算得到刚度曲线如图3所示。由图3可以看出:在±60 mm跳动过程中,Adams仿真[7]计算结果与 Matlab数学计算结果趋势接近,误差在±10%以内;在±60 mm跳动范围以外,出现的误差主要是橡胶套的刚度变化引起的;当压缩或回弹到一定高度,橡胶套的刚度出现明显变化导致刚度曲线出现突变,误差最大达到13.7%。图3可以用于说明在正常跳动的范围内本数学模型的可行性。
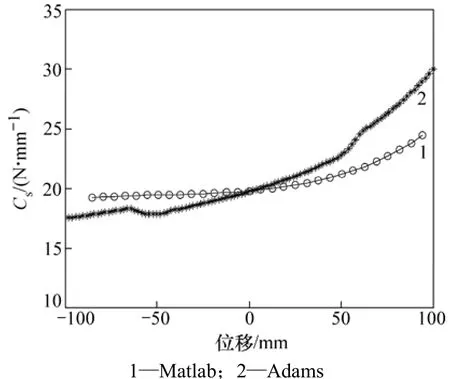
图3 悬架垂向刚度图Fig.3 Stiffness curve of the suspension
2 扭杆基本尺寸对悬架刚度的影响
在轮胎跳动过程中,由于空间导向机构运动的非线性,导致悬架刚度的非线性。为了保证悬架跳动符合总布置设计要求,前轮定位参数变化趋势较小。在保证悬架硬点坐标不变的情况下,分析扭杆直径 d、扭杆有效长度Le和扭杆预扭角度α。由于改变下横臂摆臂相当于改变悬架硬点,涉及到悬架和转向的硬点配合,因此,没有将下横臂摆臂长作为影响变量分析。下面分析参数变化范围取值为±10%时各个参数对悬架刚度的影响。
2.1 扭杆直径对悬架刚度的影响
悬架刚度随扫杆直径变化曲线图如图4所示。从图4可以看出,扭杆直径分别为25,26和27 mm时,相对于中间值26 mm变化量为3.85%,将满载时悬架刚度作为评价指标,刚度变化量为15%。
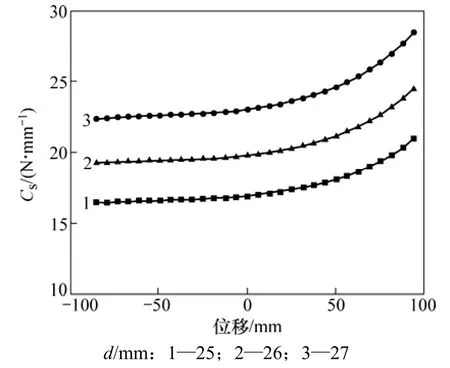
图4 悬架刚度随扭杆直径变化曲线图Fig.4 Stiffness curve of suspension with variable diameters
2.2 扭杆有效长度对悬架刚度的影响
悬架垂向刚度随扭杆长度的变化如图5所示。从图5可见:当扭杆有效长度分别为913.5,950.0和986.5 mm时,相对于中值变化量为3.85%,满载悬架刚度,刚度变化量为2.56%。
2.3扭杆预扭角度对悬架刚度的影响
悬架垂向刚度随预扭角度的变化如图6所示。从图6可见:当扭杆预扭角度分别为8.41°,8.75°和9.09°,与中间值变化为 3.85%时相比,预扭角度对悬架刚度没有影响。因为其实际上改变的是悬架下横臂的工作状态,调整悬架空间初始状态的位置,并没有改变悬架刚度曲线,只是改变了工作区间段。
从上面可以分析出对悬架刚度影响较大的参数有扭杆的直径d和扭杆的有效长度Le。
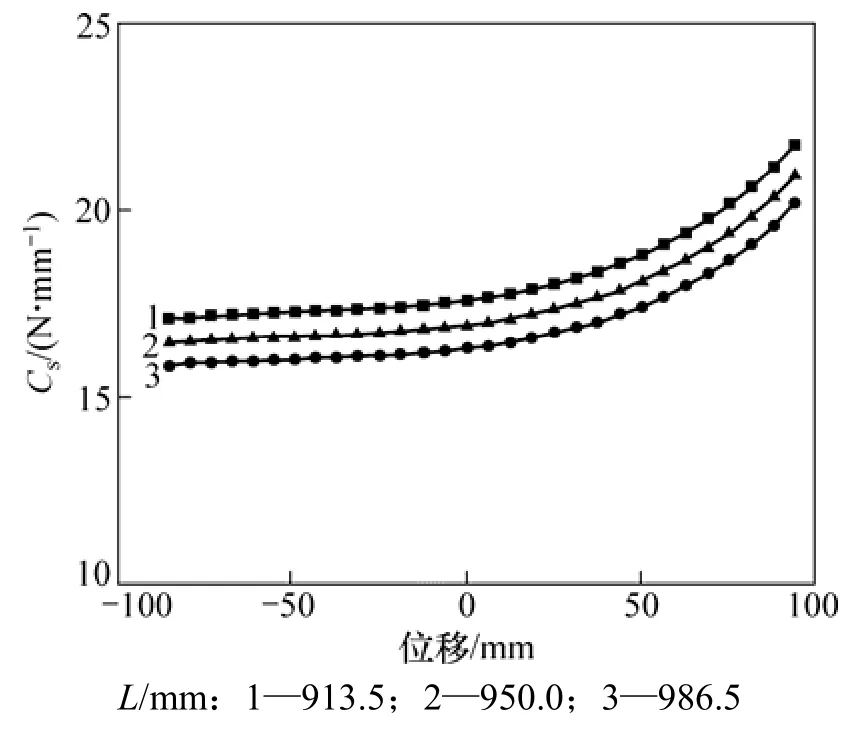
图5 悬架垂向刚度随扭杆长度变化曲线Fig.5 Stiffness curve of suspension with variable length
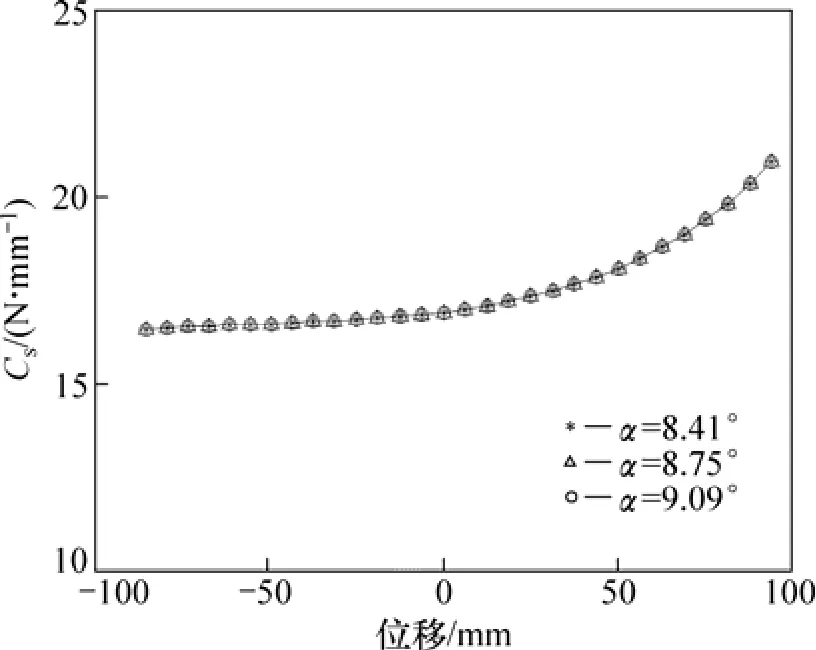
图6 悬架垂向刚度随预扭角度变化曲线Fig.6 Stiffness curve of suspension with variable angles
3 扭杆基本尺寸优化数学模型的建立
在试车过程中前悬架偏软,轮胎跳动过大,导致前轮定位参数变化比较明显,车身高度变化较为突出。所以,本文以零载至空载和空载至满载悬架垂向位移变化量作为优化目标,同时兼顾轮胎动载荷与行驶舒适性参数,优化悬架刚度时选择合适的扭杆直径与有效长度。
3.1 悬架性能参数约束条件函数的建立
考虑车辆行驶的安全性和舒适性,建立评价指标公式[7-8],分析悬架动行程参数。以频域功率谱密度作为评价指标,引入新的目标函数方法,分析空载(含驾驶员)、半载、满载3种工况下的性能指标[9]。
首先建立1/4车辆模型[10-14],如图7所示。图7中:h为路面输入;k1和k2分别为悬架刚度和轮胎刚度;c1为悬架阻尼系数;m1为车身质量;m2为车轮质量;x1为车身位移;x2为车轮位移。
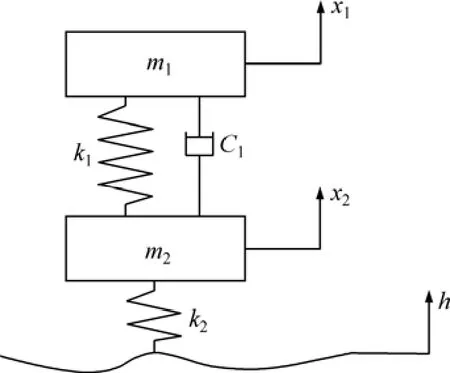
图7 车辆1/4物理模型Fig.7 1/4 physical model of vehicle
建立相应状态空间方程:
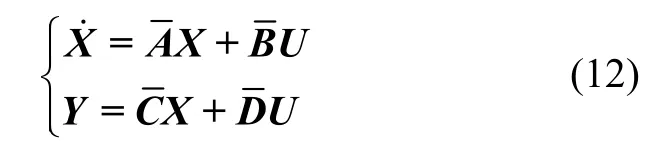
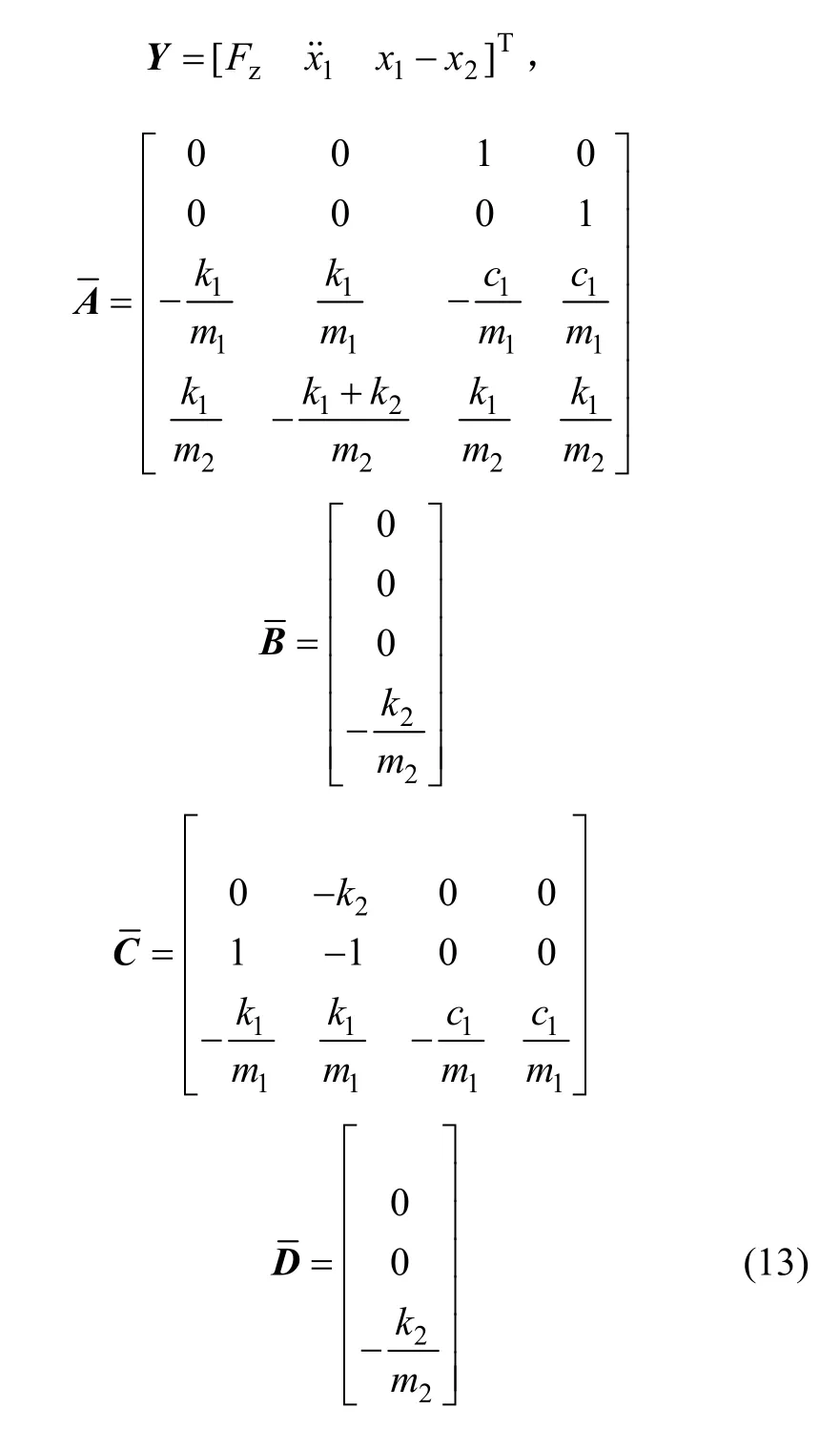
Fz为轮胎的动载荷。路面输入h为路面谱密度函数[9]:
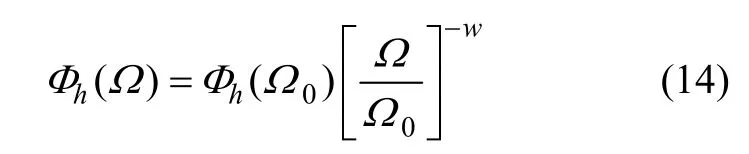
其中:Ω0为标准的行程圆频率;Φh(Ω0)为路面不平度的尺度;w为波度性尺度。
考虑行驶地点为校园、旅游景点,所以,路况较好。选择Ⅱ级路面作为参考输入,路面较平,跳动量比较小。其次,校园车速限速,速度较低。此处车速v设置为10 m/s。将路面谱行程功率谱转化为时域功率谱[14]:
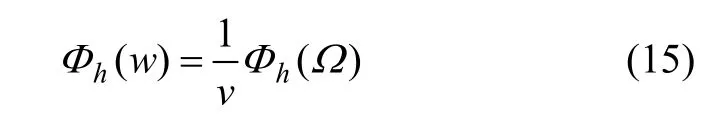
根据路面谱以及振动参数的幅频特性求出评价指标的标准差。
3.1.1 安全性
行驶安全性即轮胎动载荷Fz,定义为相对于静平衡位置的轮胎载荷变化的均方根值,可衡量轮胎附着能力的指标[15]。
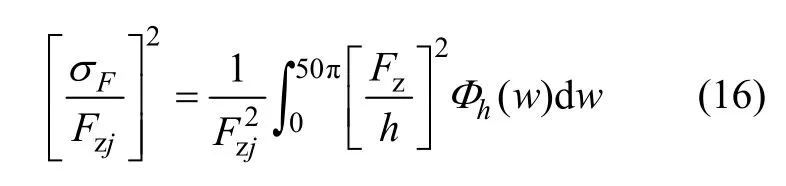
其中:Fzj表示静载荷。认为当激振频率高于25 Hz时,车身振动不能视为刚体[15],故将积分上限圆频率取值为 50π。
3.1.2 舒适性
对于轿车而言,舒适性可定义为垂向加速度的加权加速度均方根[15]:
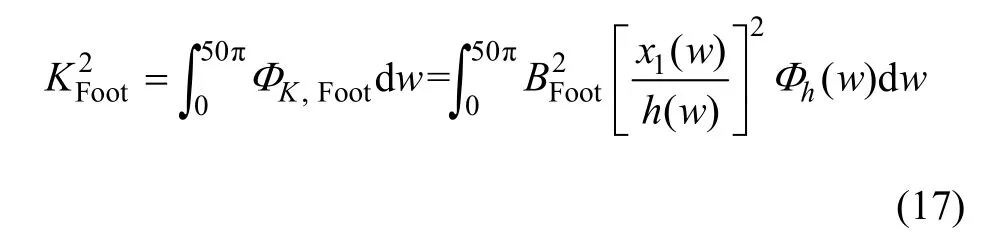
由于随机振动频率很宽,比简谐振动让人更不舒服,所以,引入1个评价函数[15],如图8所示。
BFoot=,为随机修正系数[15],如表1所示。
本文数学模型中的振动分析主要集中在脚部z方向,根据上述图标选择相应的修正系数。
3.1.3 动行程
悬架动行程可定义为车轮与车身的位移之差的均方根[16],是指在载荷不变的情况下,由路面激励引起的位移变化量。
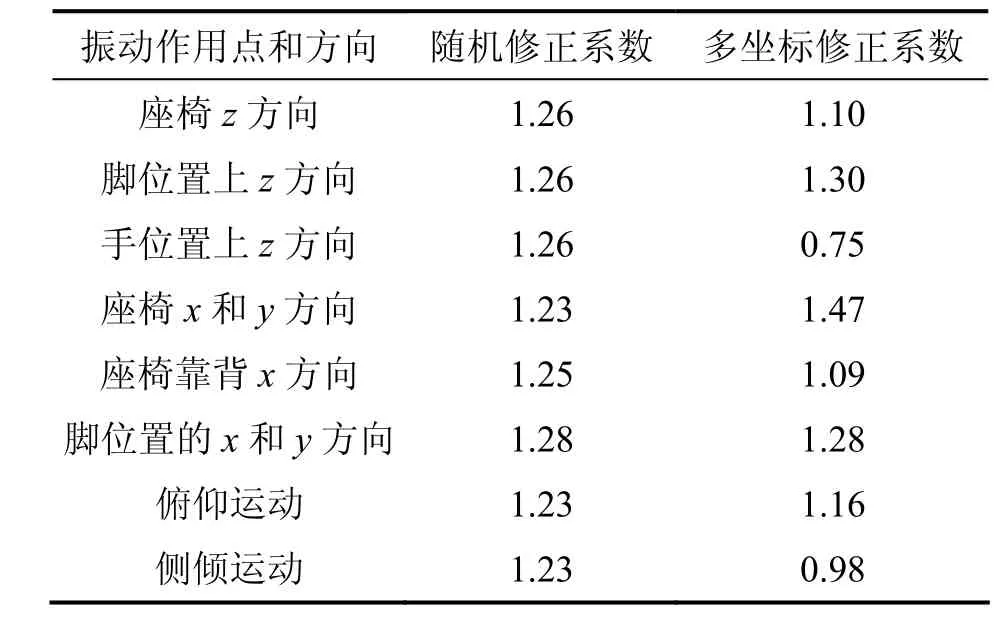
表1 修正系数Table 1 Correction coefficients
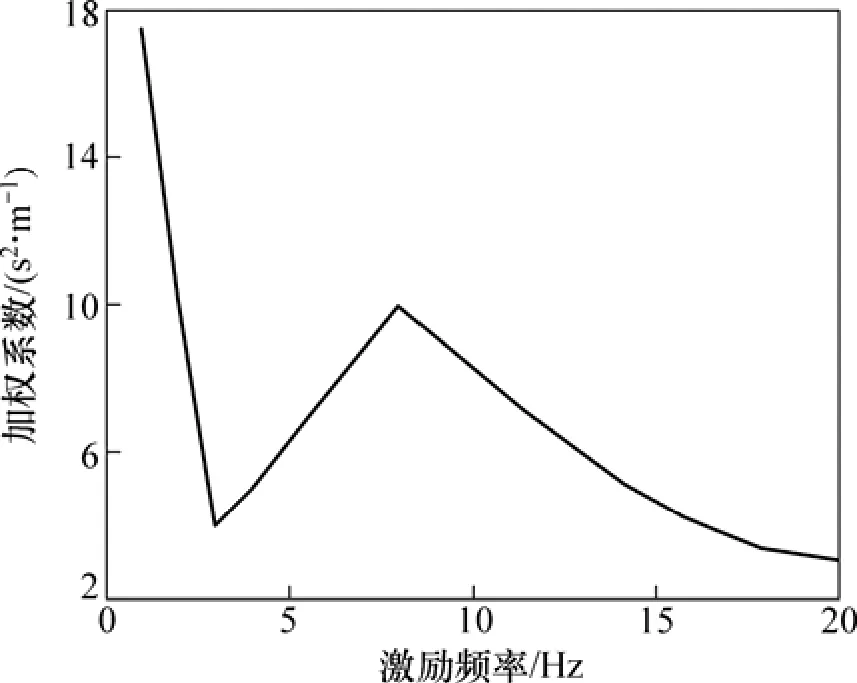
图8 振动评价指标Fig.8 Evaluation value of vibration
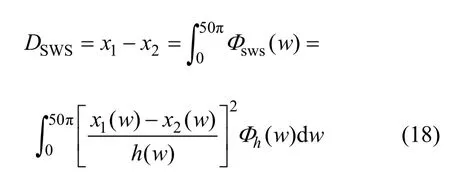
3.2 目标函数的确立
由于在试制过程中出现悬架跳动行程过大,车身高度变化较为明显,所以,以如下2个参数作为目标函数。
(1) 车辆载荷从零载至空载时,下球头点垂向位移变化量为:

(2) 车辆载荷从空载至满载时,下球头点垂向位移变化量为:

3.3 约束条件函数的确定
(1) 根据总布置的空间布置决定扭杆纵置,在长度方向限制扭杆长度为:
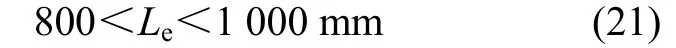
(2) 由于距车架的下表面的高度的限制,所以扭杆直径限制为:

(3) 为了便于加工,选取扭杆直径为整数或者小数末位为5的数值;
(4) 扭杆材料采用 45CrNiMoVa优质合金钢,经过喷丸处理后,扭杆的许用应力[σs]取 1 270~1 370 MPa;
(5) 轮胎动载荷变化Fz变化量尽量小;(6) 悬架舒适性参数KFoot变化范围要求尽量小;(7) 悬架动行程变化DSWS变化较小,保证碰击限位块的可能性较小。
3.4 优化结果
利用 Matlab非线性多目标优化工具箱求解得到优化结果:扭杆直径为 26.5 mm,扭杆有效长度为895 mm。
4 优化后悬架性能参数结果分析
优化前后性能参数如表2所示。由表2可知:
(1) 优化前,当悬架载荷从零载变化到空载时,主销下球头点垂向位移变化为77.5 mm,空载至满载垂向位移变化为88 mm;优化后,当悬架载荷从零载变化到空载时,主销下球头点垂向位移变化为70 mm,从空载变化到满载垂向位移为76.5 mm,垂向位移变化量分别减少9.67%和13.1%。
(2) 3个评价指标轮胎动载荷的变化量为1.35%,舒适性参数变化量为 5.83%。而悬架动行程基本没有变化。这主要是由于车辆行驶路面为校园道路,路况较好。
(3) 在基本不影响悬架性能情况下,有效减小悬架偏软现象。
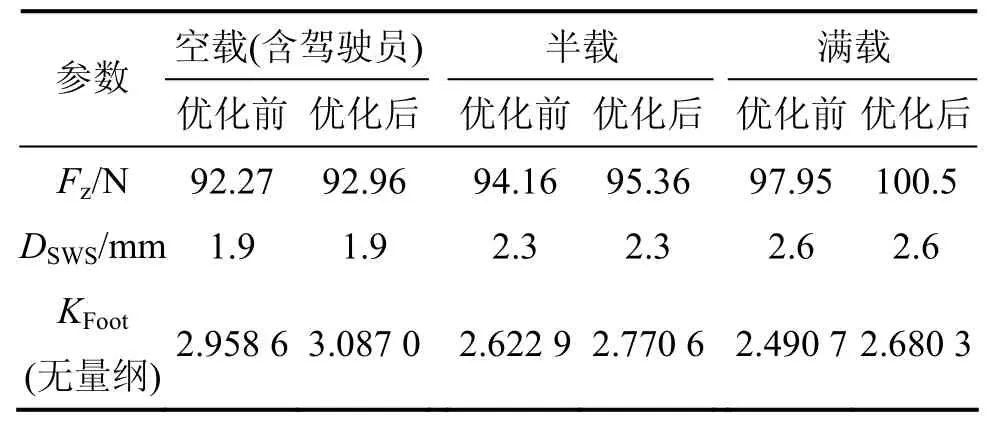
表2 优化前后性能参数Table 2 Property parameter of before and after optimization
5 结论
(1) 利用矢量代数,结合有限张量法和虚功原理用Adams软件计算双横臂扭杆悬架的刚度,证明了数学计算方法的可行性;通过计算,分析扭杆基本参数对悬架刚度的影响,并进行敏感度分析得到文中需要优化的基本参数。
(2) 根据车辆实际行驶道路状况,提出以轮胎动载荷、悬架动行程和舒适性参数作为约束条件,以悬架跳动量作为目标函数和指标,建立双横臂扭杆悬架的扭杆基本尺寸的优化模型。
(3) 通过Matlab多目标优化工具箱优化扭杆基本尺寸,使悬架从零载至空载悬架垂向位移行程减少9.67%,空载至满载垂向位移减少13.1%,有效增加了悬架刚度,减少了悬架限位块经常被碰击的现象;同时,限制前轮定位角的变化,在不影响悬架性能的前提下有效改善了汽车前悬架偏软的现象。
[1] 韩锐, 毛务本. 矢量代数在双横臂独立悬架中运动分析中的应用[J]. 公路交通科技, 2003, 20(6): 139-142.HAN Rui, MAO Wu-ben. Vector algebra in kinematics analysis of the dual wishbone independent suspension[J]. Journal of Highway and Transportation Research and Development, 2004,34(4): 139-142.
[2] 岳惊涛, 陈定坤. 双横臂扭杆悬架的刚度计算及负荷特性分析[C]//中国汽车工程学会 2008年会论文集, 天津: 机械工业出片社, 2008: 300-303.YUE Jing-tao, CHEN Ding-kun. Stiffness calculation and load characteristic analysis of double wishbone independent suspension with torsion bar[C]//Proceedings of Society of Automotive Engineers China, 2008. Tianjing: China Machine Press, 2008: 300-303.
[3] 丁飞, 韩旭 .悬架导向机构硬点灵敏度分析及多目标优化设计[J]. 汽车工程, 2010, 32(2): 138-142.DING Fei, HAN Xu. Hardpoints sensitivity analysis and multi-objective optimization of suspension guiding mechanism[J]. Automotive Engineering, 2010, 32(2): 138-142.
[4] 陈黎卿, 陈无畏. 双横臂扭杆独立悬架多目标遗传优化设计[J]. 中国机械工程, 2007, 18(17): 2022-2025.CHEN Li-qing, CHEN Wu-wei. Multi-objective heredity optimization design of torsion-bar wishbone suspension[J].Chinese Mechanical Engineering, 2007, 18(17): 2022-2025.
[5] 曾迥立. 双横臂独立悬架线刚度的非图解法计算[J]. 汽车工程, 2006, 28(8): 747-749.ZENG Jiong-li. A non-graphic method of calculation line stiffness of the double wishbone independent suspension[J].Automotive Engineering, 2006, 28(8): 747-749.
[6] 洪嘉振. 计算多体系统动力学[M]. 北京: 高等教育出版社,2009: 38-40.HONG Jia-zhen. Computational dynamics of multibody systems[M]. Beijing: Higher Education Press, 2009: 38-40.
[7] 宁国宝, 张立国. 双横臂扭杆弹簧悬架空间结构非线性的建模与分析[J]. 汽车工程, 2010, 32(2): 143-147.NING Guo-bao, ZHANG Li-guo. Modelling and analysis of nonlinear characteristics of spatial structure in double wishbone suspension with torsion bar[J]. Automotive Engineering, 2010,32(2): 143-147.
[8] 时培成, 韦山. 双横臂扭杆弹簧悬架刚度计算及动态仿真[J].机械工程师, 2006(8): 43-45.SHI Pei-cheng, Wei Shan. Simulation and calculation of the double wishbone suspension with torsion bar[J]. Mechanical Engineers, 2006(8): 43-45.
[9] 唐应时, 柴天. 基于接触摩擦的少片变截面钢板弹簧的刚度分析[J]. 中南大学学报: 自然科学版, 2009, 40(3): 693-698.TANG Ying-shi, CHAI Tian. Analysis of stiffness of taper leaf spring based on contact frication[J]. Journal of Central South Univerity: Science and Technology, 2009, 40(3): 693-698.
[10] 兰波, 喻凡. 车辆主动悬架 LQG控制器的设计与仿真分析[J]. 农业机械学报, 2004, 35(1): 13-17.LAN Bo, YU Fan. Design and simulation analysis of LQG controller of active suspension[J]. Transaction of the Chinese Society for Agricultural Machinery, 2004, 35(1): 13-17.
[11] Liu Z, Angeles J. Least-square optimization of planar and spherical four-bar function generator under mobility constraints[J]. ASME: Journal of Mechanical Design, 1992,114(4): 569-573.
[12] Suh C H. Synthesis and analysis of suspension mechanisms with use of displacement matrices[C]//Proceedings of Society of Automotive Engineers, USA, 1989: 189-200.
[13] Ramon Sancibrian, Pablo Garcia. Fernando Viadero. Suspension system vehicle design using a local optimization procedure[C]//In Proceeding of ASME (2005) 29th International Design Engineering Technical Conference. California, 2005:227-236.
[14] Rao S S. 机械振动[M]. 4版. 李欣业, 张明路, 译. 北京: 清华大学出版社, 2009: 644-672.Rao S S. Mechanical vibration[M]. 4th ed. LI Xin-ye, ZHANG Ming-lu, trans. Beijing: Tsinghua University Press, 2009:644-672.
[15] Mitschke M. 汽车动力学[M]. 陈荫三, 余强, 译. 清华大学出版社, 2009: 259-274.Mitschke M. Vehicle dynamic study[M]. CHEN Yin-san, YU Qiang, trans. Beijing: Tsinghua University Press, 2009:259-274.
[16] ISO 2631. Guide for the evaluation of human exposure to Whole-body Vibrations[S].
