二胡副弦与狼音

韩佩琦，高新存，王文武

（1.河北科技大学理学院 ，河北 石家庄050018；2.河北地质职工大学，河北 石家庄050018 ）

1 引言

《演艺科技》2011年第三期《二胡琴皮的振动与狼音的关系》重点分析了琴皮与琴弦发生共振时，就可能引发狼音。即琴皮固有振动中各次泛频间的不和谐性是产生狼音的因素之一。本篇主要分析狼音的另一个形成因素——副弦的振动。

2 对副弦振动的讨论

为方便计，讨论没有加音垫的二胡，并把二胡琴弦分为三段。如图1所示。第一段 l0为千斤至琴轴的距离，它基本不参与振动；第二段 l 是千斤至琴马的距离，因为二胡的基本乐音靠它策动引发，故称之为有效弦长，它的振动称之为基本振动，其基频率以 f 表示；第三段 l' 为琴托至琴马的距离（即副弦），它的固有振动频率的基频以 fg表示。

2.1 有效弦长的基本振动

在一般演奏原理的讨论中，人们主要关心的是最能体现二胡音色的基本振动，因为弓毛摩擦琴弦 l ，使之振动并传至琴马，而琴马以简谐力的方式压迫琴皮做同步振动，推动空气振动，再经琴筒予以共鸣放大，使二胡的乐音传到人耳。所以这样的讨论着眼点是有效弦长 l 的振动。需要指出，为突出主要矛盾，这里总是把千斤以及琴马视为理想的固定点，进而得出弦振动频率基本公式：

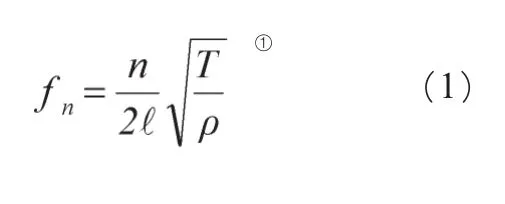
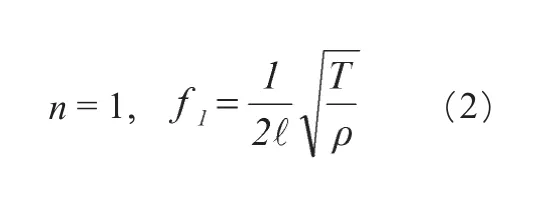
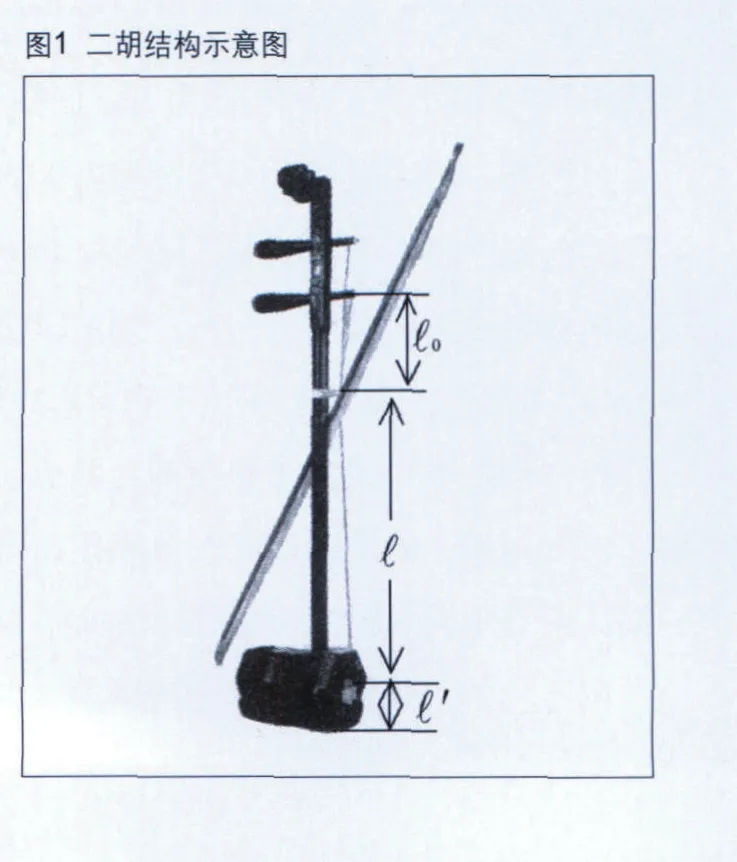
f1是弦振动的最低频率，称为弦的基频，n 〉1的各次振动频率称为泛频，例如n＝2时，f2称弦的第一泛频，余类推。因为是固定的，于是在定好调以后，其振动频率与弦长 l 构成一一对应的关系，（2）式即是各种调式把位指法图的理论根据。演奏时由于手指触弦位不断地变化，即不断地改变着有效弦长l，才会奏出不同频率的音符。无论是滑音、揉弦、颤指等都遵循着上面的弦振规律。可见这样的讨论把琴马视为固定点是有道理而且也是必要的。

2.2 副弦的固有振动及与透射波的叠加

当探求狼音来源时，需要对副弦 l' 的振动进行讨论。

在讨论副弦受激而引发的固有振动频率时，需要把马子视为“固定点”，而在注意到基本振动通过琴马透射到副弦上的时候，则必须承认琴马相当于一个简谐振动源。

2.2.1 副弦因琴马激励而引发的固有振动（琴马上实际存在的几种振动）

一段两端固定而被绷紧的弦，受到任何激励或扰动都会引发受激振动。一方面，二胡琴马相当于副弦 l' 的上固定点，而在演奏二胡过程中，由于琴马被有效弦长 l 激励而作简谐振动，于是琴马又激励了副弦的振动，而这个受激振动的基频即是 l' 的固有振动基频 fg，且

由于任何一把二胡演奏时琴马在琴皮上的位置是固定的，即 l' 固定，所以其固有频率 fg不会随着激励信号的频率做任何变化。

另外，有效弦长 l 振动时，驱使琴马在琴皮上做简谐振动，这相当于在 l' 端点存在着一个简谐策动源，它一方面激励 l' 做固有振动，又同时把简谐振动传递（透射）过去。这样导致 l' 上实际存在着两种同方向不同频率的振动的叠加。由于 l' 上实际存在着两种同方向不同频率的振动的叠加，这正是应该讨论的关键问题。因为这两个同方向不同频率的振动的叠加，其合振动已不再是简谐振动，然而却有周期性。合振动的频率用 ffg表示。其周期一般称之为主周期Tfg，主周期Tfg是两个分振动周期的最小公倍数②。当T=nTg时，T 即是最小公倍，即主周期。实际上，由于诸多不确定因素一般很难保证恰好满足T=nTg，但可以肯定在所讨论的范围内基本满足T＞Tg。为突出主要问题和方便讨论，可设T=nTg，则叠加振动的主周期Tfg=T。

由于 l' 两端固定，这叠加的振动在琴弦上形成叠加的波，沿副弦传到底座又会经底座反射回琴马。如此看来，琴马上存在着以下几种振动。

（1）有效弦长 l 受琴弓摩擦所产生的基本振动 f，此振动振幅最大。

（2）副弦 l' 受琴马基本振动的激励而产生的固有振动fg，振幅很小。

（3）由琴托反射回来的叠加振动 ffg，振幅很小。

2.2.2 副弦上叠加振动的周期与副弦固有周期的比值计算

为了有个量化的概念，下面计算合振动的频率或周期。为方便计，可设 l' 上的固有振动和经琴马透射过来的振动相位相同。

l =40 cm， l' =7.5 cm，设二胡五度定弦，在D调演奏时，外弦空弦为5，频率为446 Hz③，则由，即

由此可得出 C＝0.8×446=356.8 m/s

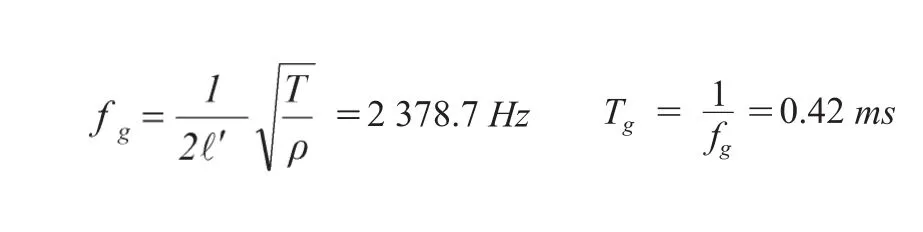
按D调计算外弦各音符的相关数据，见表1。

由表1数据和理论分析可知，在副弦上叠加而成的振动具有明显的特点：

（1）非正弦振动的主周期 Tfg与有效弦长振动的基频周期T相同，但每个主周期都是 Tg的若干倍，即其中包含了频率更高的成分 fg。

（2）副弦上叠加振动的周期＞ Tg，一般是它的几倍以上。

（3）由此引发的波形必然也是周期性非正弦波。

又因为在演奏中两个振动始终存在，固有振动频率不变，而 l 会随着演奏触弦位的变化而变化，即所叠加的基本振动的频率是不断变化的，于是就决定了合振动的周期也在不断地变化着。规律是 l 越短演奏的乐音越高，合成的频率就越高，其周期也就越短。由于琴皮属于薄膜振动类，演奏过程中它所做的是受迫振动，一旦在某个音位叠加的 ffg等于或接近琴皮的固有频率fq之时，必然会出现共振效应。由于基频f中包含有更高的频率成分fg，这fg的作用相当于对f进行了调制或把波形进行了切割，即本来振幅很小的噪波会被突然放大，这种被突然放大的周期性非正弦波显然是不和谐的声音，它被突然放大后以噪波（沙粒般的刺耳怪音）表现出来——这就是我们所说的狼音。又由于具有周期性，所以从理论和听觉上都可知道它具有一定的音区归属感。它往往对应琴弦l上某一确定的位置。

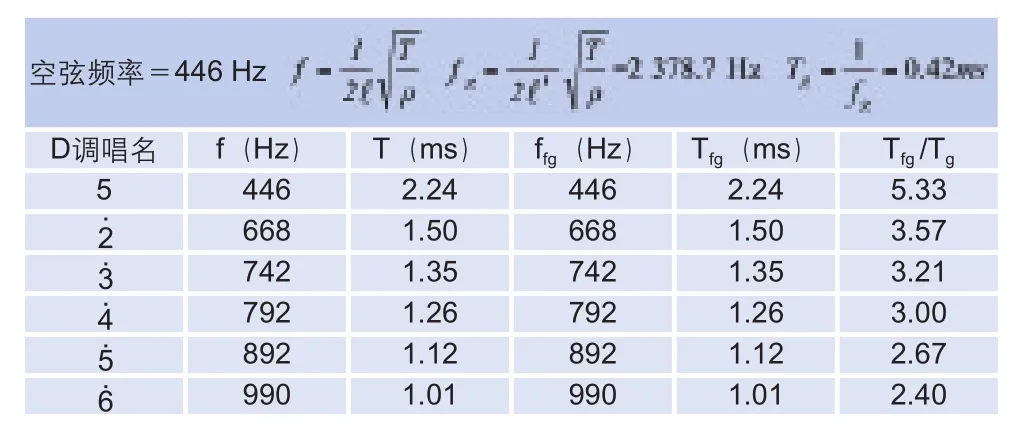
表1 叠加振动的周期Tfg与副弦固有周期Tg的比值

3 实验现象及其理论解释

3.1 通过存储式示波器和声电转换器件观测二胡音域内的频谱

可以发现在狼音位具有明显尖锐的共振峰，且可看到狼音位包含的噪波不仅振幅较大，而且明显为畸形波。而从狼音位以外的其他位置可以看出，在正常的基本振波里包含有振幅较小的噪波（周期性非正弦波）。因振幅很小，听觉上仍然是基本的乐音，但其声音的柔美程度已不甚理想。

3.2 狼音具有音区归属感的实验

一般而言，当二胡定好调（A、D）之后，狼音在琴弦上的位置是固定的。在演奏中通过手指触弦很容易找到，这样可知道狼音所归属的音区或频率范围，比如在C调 的位置出现狼音，则知其频率位置是880 Hz。当调节琴轴，使琴弦所受张力T改变，由（2）式可知是改变了琴弦的固有频率f。可以看到狼音在琴弦上的位置会随着T的变化而改变，但却始终对应着一个不变的频率。比如加大T，狼音位置将在琴弦位置上上移，而降低T，狼音位置将在琴弦位置上下移。由于琴皮的固有振动频率fq不变，而只有副弦上叠加的振动频率ffg近似等于fq时，才会引起琴皮的共振效应，才会出现狼音。因而可知，狼音的频率基本上与琴皮固有频率的基频fq相同。当然，也可由狼音所处琴弦的位置推知狼音的频率。

3.3 狼音的抑制实验

一人在拉奏出二胡狼音时，另一人以手指压或勾住副弦的外弦，即可听到狼音顿然消失。这里是抑制了副弦的振动，使副弦上的固有振动以及透射波全部消失，才使得狼音得到了抑制。这启示人们如何从根本上抑制狼音。

另外，当某人手勾或压迫副弦的外弦，另一人如果一直演奏，尽管狼音位上明显的狼音已经消失，但在其他音位（包括里外弦）甚至整个音域上，都伴随着微弱的噪音，即在听觉上远不如加绒布音垫之后的音色柔和。这是由于副弦也存在着两种振动的叠加，只不过其频率相对琴皮的频率fq较低，没被放大，但却包含在基本乐音振动波形当中，故而有微弱噪声。但当把副弦里外弦全部勾住演奏时，不仅能使声音柔和，而且音量也比加音垫之后大。这无疑提供了一种抑制狼音和消噪的设计思路。

最后应提及传统音垫的作用，由于它被两根琴弦压住，或说音垫把两根副弦紧密地顶起，不仅抑制了副弦的固有振动，同时也把琴马上的透射波吸收了，这无疑起到了抑制狼音的积极作用，但由于音垫所需要的支持力来源于琴皮，它对琴皮的压力构成了琴皮振动的较大阻尼，使琴皮的振幅减小，所以音垫的消噪作用是以牺牲音量为代价的，因而这是音垫的消极一面。如何能在不降低音量的前提下有效地抑制狼音，期待同行智者见智。

注释：

① 韩佩琦，王文武，刘天山，高新存.弦振泛频分析及演奏中的泛音[J].河北科技大学学报，2007，28（3）

② 漆安慎，杜婵英.力学.北京：高等教育出版社，1997：270-271

③ 人民教育出版社物理室编著.物理学.（第一册）.北京：人民教育出版社，1995.12.第159页