基于模糊神经网络的驼峰推送速度控制研究
2011-07-30马立君
马立君
*南京铁道职业技术学院 助教,210015 南京
现代自动化驼峰系统包括机车推送速度的遥控、溜放进路自动控制、溜放速度自动控制、编组站信息综合系统等主要技术。在目前的技术条件下,推送机车已成功使用了无线遥控技术,并与溜放速度的自动控制系统联成整体。如能在将列车解体、推送、溜放作业视为一体的条件下获得最佳推送速度,可实现驼峰调速的整体优化。
在推峰速度由人为给定的控制方式下,机车推送速度的大小是凭个人的经验给出,不易保证获得最优的推送速度;且车组溜放过程是一个复杂的多变量系统,受到众多因素如气候、车组等影响,溜放过程的实时性和车辆走行状态的不确定性,使得溜放速度的控制模型的建立和求解有一定困难。应用模糊神经网络理论建立求解机车推送速度的模型,不需要建立精确的数学模型,利用动态推理神经网络构成的模糊控制系统,模拟人的实际思考和操作过程,就能确定推送速度。该方法既兼顾了机车推送速度控制知识中的模糊性,又利用了神经网络自学习能力强的特点,易于将专家或熟练操作员的控制策略转换为功能函数,可根据实际溜放情况实现动态计算机车的推峰速度。
1 基于模糊神经网络确定的推送速度
神经网络模糊控制器是由神经网络和模糊控制共同组成的混合系统,兼备两者优点。通过利用神经网络记忆模糊控制规则的方式,为模糊控制器提供学习功能,自动生成模糊控制规则,将规则隐含地分布在整个网络之中,利用离线训练之后满足要求的网络,通过在线计算得出优化的输出结果。
1.1 模糊神经网络变速推峰模型
为保证相邻车组之间良好的间隔,调速时既要考虑影响本车组走行性能的因素,还要考虑前行车组和后续车组的速度等。为使系统简单,应尽量合并有耦合关系的变量。通过分析现场操作数据,确定了如下几个影响推送速度的因素。
1.车组长度。当假定机车以恒定速度V0推送机车时,车组的长度就决定了相邻车组通过峰顶的间隔时分t0。根据溜放作业的需求,当确定了所需的t0后,车组越长,推送速度就可以越高。因此可以预先根据车组长度条件规定不同的推送速度。
2.相邻车组分歧道岔位置。相邻车组分歧地点近,前后钩车共同走行的线路区段则较短,在较短的线路区段保持车组的间隔比较容易,因此可以适当提高V0。
3.相邻车组走行性能的差异。用车组的重量估计其走行性能,即认为重车为易行车,轻车为难行车。车组在加速坡溜放时,加速坡短而陡且道岔阻力和曲线阻力都比较小,可以认为车重是钩车走行性能的最重要影响因素。另根据阻力总体回归分析结果,车辆总重对阻力的影响最大,温度次之,速度的影响最弱,因此推送时着重考虑车重因素。
从以上分析可得,影响推送速度的主要因素作为系统的输入参量,被控参量即推送速度则作为系统的输出。图1给出了推送速度神经网络模糊控制框图。
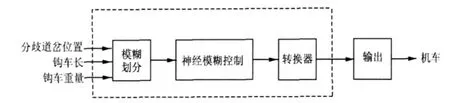
图1 推送速度神经网络模糊控制框图
驼峰机车推峰速度神经模糊控制器在输入/输出参量的选择、在模糊论域和模糊子集的确定方面,与一般的模糊控制器没有什么区别,只是在推理手段上引入了神经网络。本系统构造了一个三层BP网络,输入结点为15个,根据Kolmogorov定理,确定中间层结点为2×15+1=31个,输出层结点为5个,各层之间的传输函数均采用Sigmoid函数。
系统的工作过程如下:分析计算影响推送速度的几个主要因素,传输到模糊化模块,对其进行模糊化处理,求得其对应各模糊子集的隶属函数。将这些隶属函数作为动态模糊推理网络的输入向量,经过动态模糊推理网络进行推理、决策后输出相应的模糊输出向量,然后经过精确化处理后得到优化的机车推送速度。
1.2 输入变量的模糊化处理
分析现场操作数据,依次对各变量进行模糊化处理,确定各变量的论域、语言变量和隶属函数。对于不同的编组站,由于站场设计的不同,论域和隶属函数的参数也可能存在差异。
1.钩车重量。论域为 [40,60],单位为吨。赋予4个语言变量值,即“轻”、 “较轻”、 “较重”、“重”。隶属函数采用模糊逻辑工具箱内置的Z型、S型及高斯型联合分布。
2.钩车长度。论域为 [1,8],单位为辆。赋予4个语言变量值,即“短”、 “较短”、 “较长”、“长”。隶属函数采用梯形分布。
3.分歧道岔位置。论域为 [1,90],根据驼峰场形状及道岔由驼峰方向开始由近及远命名的规则,直接取道岔号为参量,将前后两钩车所经过的所有分路道岔号逐一进行比较后取小,即可得前后两钩车分歧道岔的道岔号。为分歧道岔位置赋予3个语言变量,即“近”、“中”、“远”。将加速坡至第一制动位之间的分歧道岔定义为分歧地点“近”,将第一制动位至第二制动位的分歧道岔定义为分歧地点“中”,将第二制动位之后的分歧道岔定义为分歧地点“远”。隶属函数采用梯型分布。
4.推送速度。论域为 [4,8],单位为km/h。赋予5个语言变量,即“低”、 “较低”、“中”、“较高”、“高”。隶属函数采用高斯分布。
1.3 BP网络误差反向传播算法
1.3.1 BP网络正向和反向传播
正向传播:输入的样本从输入层经隐层单元一层层进行处理,通过所有的隐层之后,则传向输出层;在逐层处理的过程中,每一层神经元的状态只对下一层神经元的状态产生影响。在输出层把现行输出和期望输出进行比较,如果现行输出不等于期望输出,则进入反向传播过程。
1.3.2 BP算法执行
1.对权系数wij置初值;
2.输入所有样本集并对应得到期望输出;
3.由前面所述的BP算法,计算各层输出;
4.求整个网络的误差E;
5.判断误差E,若满足给定品质指标要求,则结束学习;若不满足要求,则进行第6步;
6.修正权系数和阈值,转入第3步。
1.4 输出结果的去模糊化
从模糊控制规则得到的是模糊量,须将模糊量精确化。一条规则的输出反映该条规则的激活程度,其数值为模糊变量V0中某个模糊值的隶属度值。设与V0对应的隶属函数的中心点 (平均值)为mi,则应用加权平均判别的清晰化方法求出输出V0的清晰值,如式 (1)所示。
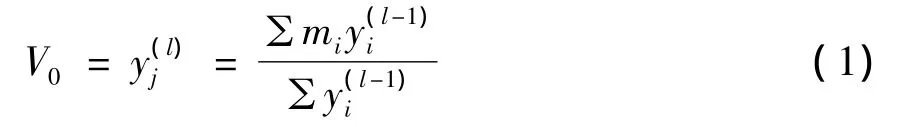
其中l为神经元的层数,yi、yj为该层权重。
2 仿真训练及研究
2.1 样本数据的选取
数据收集源于TW-2驼峰自动化系统编组现场实时操作记录,选取数据构成训练样本对,对构造的模糊神经网络进行训练。部分现场操作数据如图2所示。
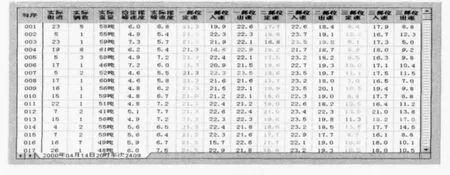
图2 驼峰溜放速度控制计划表
从溜放速度控制计划表可以看到,对于生产现场实际推送速度控制,是影响溜放速度的各主要因素,包括钩车重量、钩车长度、分歧道岔位置等,根据操作人员的实际溜放经验确定出理想的钩车推峰速度。现场操作数据在一定程度上反映了操作人员的经验和策略,从中选取具有代表性的数据进行模糊神经网络的训练,从而使训练过的模糊神经网络记忆这些经验并自动生成一系列的模糊控制规则,能够根据这些规则给出合理的推峰速度。
根据选取的数据及定义的模糊分布,输入模糊化之后构成样本集中的输入矩阵P即目标样本及输出矩阵T即目标矢量。给出部分训练样本 (2~6钩车)的目标矢量T即推峰速度构成如下。
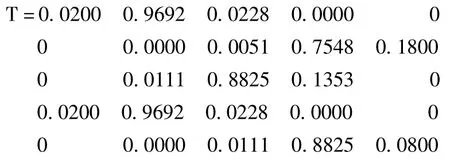
2.2 神经网络的训练
使用MATLAB神经网络工具箱函数构造如前所述的3层BP网络。定义学习算法中训练目标误差为0.001,训练步数为1000次。训练函数采用动量及自适应的梯度递减训练函数traindx。
网络经过训练后,目标误差达到要求,结果如图3所示。
针对网络的输入,使用神经网络Sim函数计算网络的最后输出A部分数据 (2~6钩车)如下。
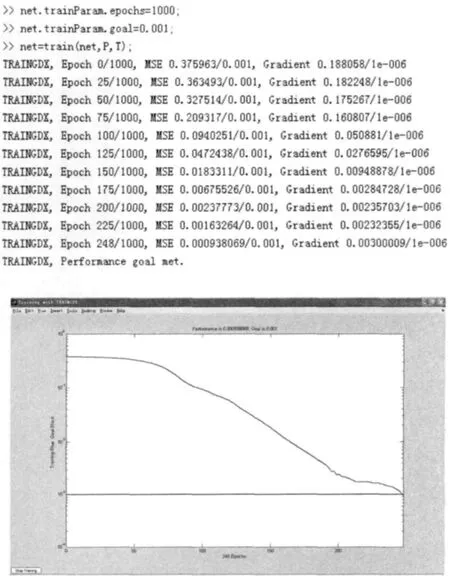
图3 仿真结果输出
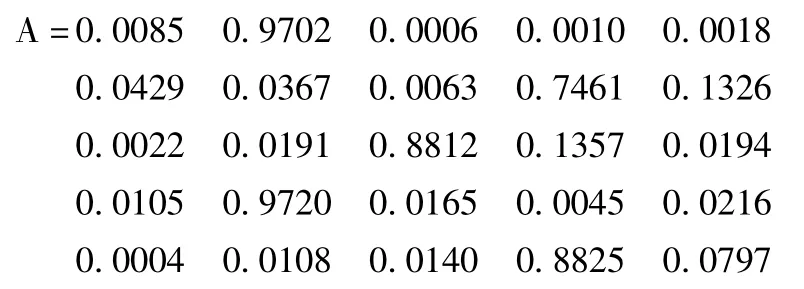
通过该数据可以看出实际训练A与期望值T总体来说偏差很小,表明该模糊神经网络较好地反映了控制规律,训练结果比较理想。
利用动态推理神经网络构成的模糊控制系统能够更好地模拟人的实际思考和操作过程,将传统的操作人员凭经验遥控机车推送速度用动态模糊推理神经网络来替代,使系统的调整过程更符合实际的溜放情况,以达到优化控制效果的目的。
[1]吴芳美.编组站调车自动控制[M].北京:中国铁道出版社,2004
[2]杜绪生,高树允.滚动轴承车辆溜放阻力的测试及研究[J].减速顶与调速技术,2003,3:2 -4.
[3]葛哲学,孙志强.神经网络理论与MATLAB R2007实现[M].北京:电子工业出版社,2007
[4]罗四维.大规模人工神经网络理论基础[M].北京:清华大学出版社,2004.
