数学形态学和HHT在轴承故障诊断中的应用
2011-07-26和卫星许莉
和卫星,许莉
(江苏大学 电气学院,江苏 镇江 212013)
滚动轴承是旋转机械中应用最广泛的部件,其运行状态是否正常将直接影响到整个机组的性能。据统计,旋转机械的故障有30%是由轴承故障引起的[1]。轴承发生局部损伤时,在其受载运转过程中,其他零件会周期性地撞击损伤点,产生瞬态冲击脉冲力,形成冲击激励产生的非平稳减幅振荡。减幅振荡的频率即为故障的特征频率,根据故障的特征频率可以对其进行故障诊断,并确定故障模式。
现场采集的振动信号经常受到随机脉冲和白噪声的影响。与传统的数字滤波器相比,形态学滤波器能够克服时滞、非线性相移等缺点,并且完全在时域中进行计算,算法简便易行、实用有效。形态滤波算法虽具有很强的抑制脉冲干扰的能力[2],但滤除白噪声的能力却不及小波算法。小波变换对白噪声有很强的抑制能力,但不能有效地抑制脉冲噪声。基于以上原因,在对信号进行数学形态学滤波之前先进行小波消噪,可以在有效消除信号干扰噪声的同时保留信号的特征。将滤波后的信号用经验模态分解(Empirical Mode Decomposition,EMD)方法分解为多个平稳的固有模态函数(Intrinsic Mode Function,IMF)之和,再用HTT(Hilbert-Huang)变换得到边际谱,进而提取滚动轴承故障特征。
1 数学形态学
1.1 基本原理
数学形态学最初是用于数字图像的处理和识别,目前已广泛应用于信号处理领域。数学形态学在考察信号时,需要设计一种收集信号信息的“探针”,称为结构元素。通过在信号中不断移动结构元素,便可以提取有用的信息进行特征分析和描述[3]。数学形态学对信号的特征提取完全在时域中进行,且形态变换计算不涉及乘除运算, 与传统的处理方法相比实时性好、时延小[4]。
数学形态学中最基本的变换是腐蚀,膨胀,开和闭。
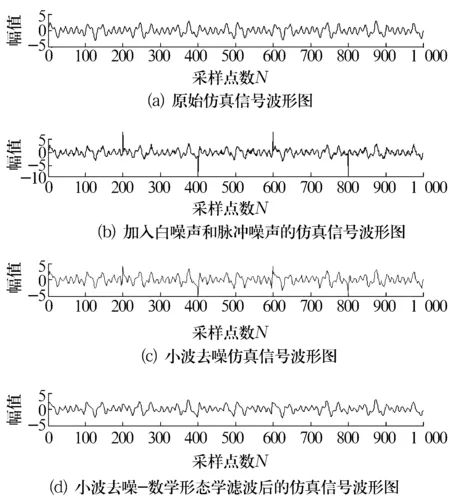
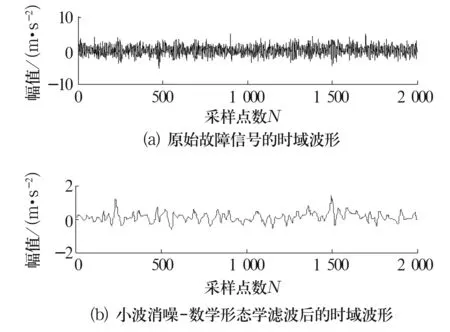
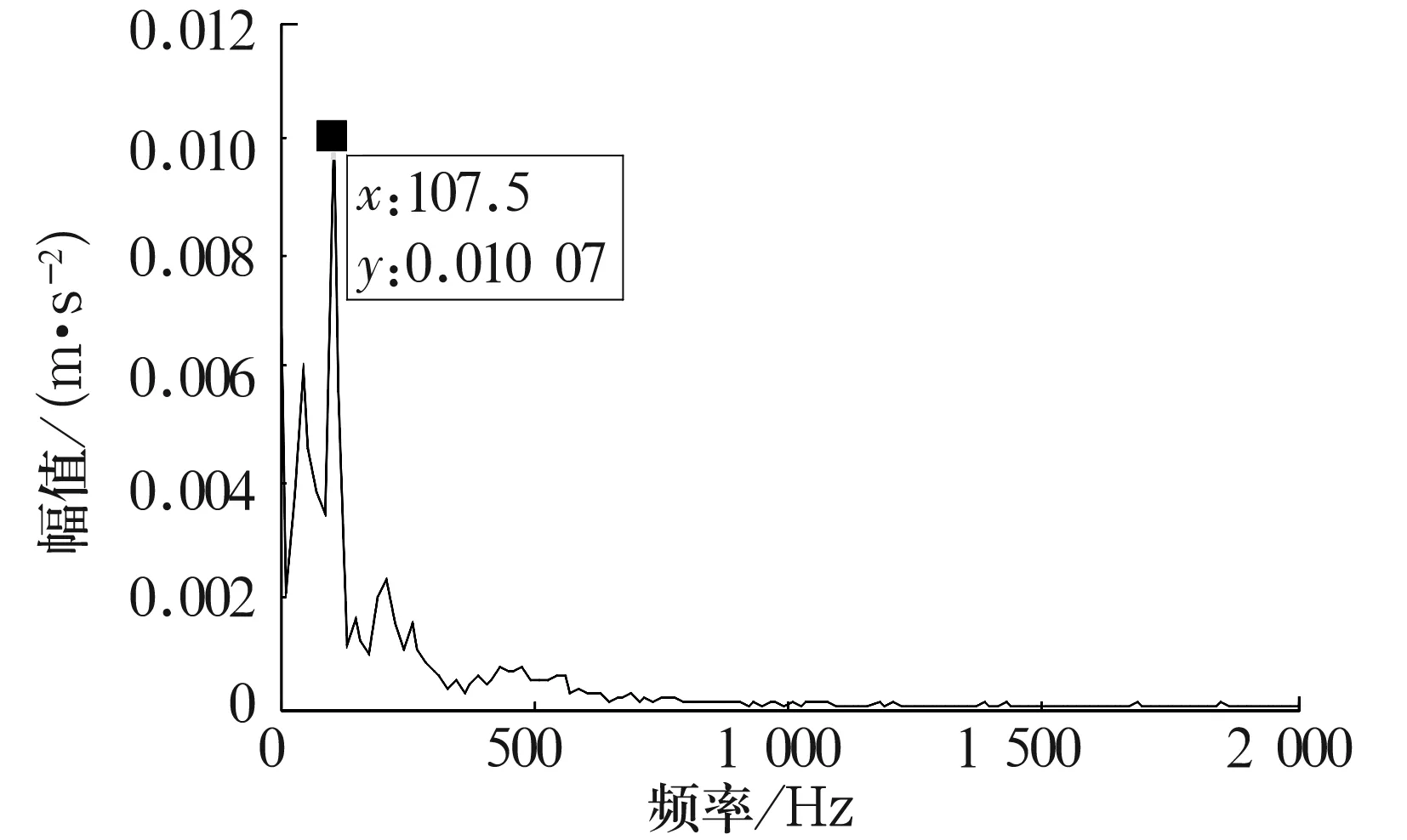
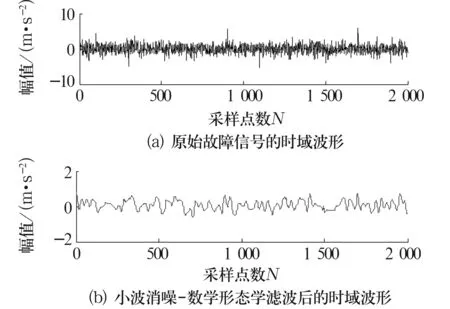
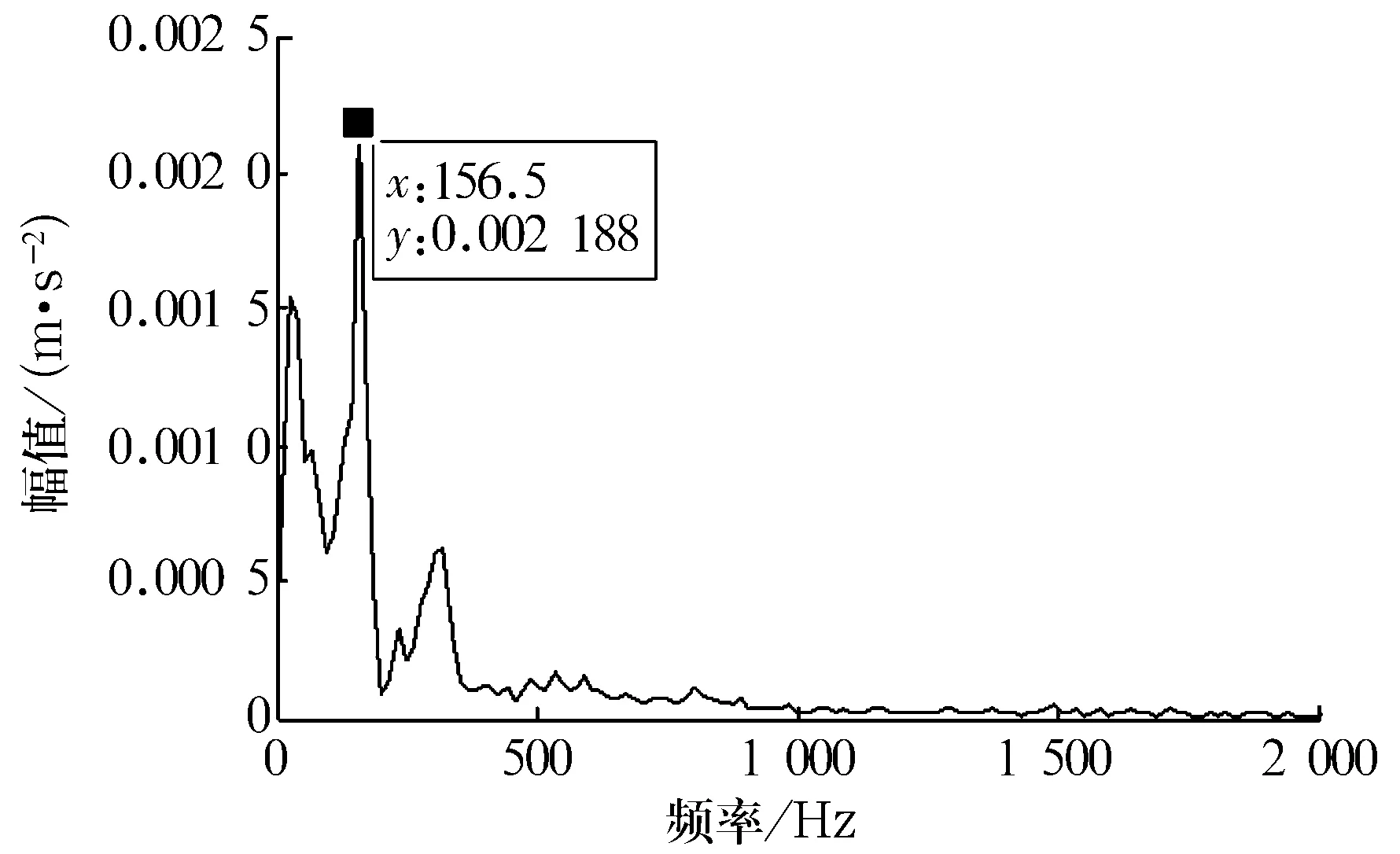
设f(n)为一维多值信号,g(n)为结构元素。H,K分别是f(n)和g(n)的定义域,H=(0,1,…,n-1),K=(0,1,…,m-1),且m (f⊕b)(n)=max{f(n-m)+g(n)}, (1) (fΘb)(n)=min{f(n+m)-g(n)}, (2) 式中:m∈K。 形态开运算和形态闭运算的定义为 (f°g)(n)=[(fΘg)⨁g](n), (3) (f•g)(n)=[(f⨁g)Θg](n)。 (4) 形态闭运算具有扩展性,形态开运算具有反扩展性,这会导致开-闭滤波器的输出幅度偏小,而闭-开滤波器的输出幅度偏大。为了减小这种统计偏移现象,采用改进型形态开-闭和形态闭-开滤波器[5]。即:设f(n)为一维多值信号,定义域F=(0,1,…,n-1),定义2个结构元素g1(n)=0(n∈G1),g2(n)=0(n∈G2),G1的宽度小于G2的宽度。则, Eoc=f(n)ΘG1⨁G2, (5) Eco=f(n)⨁G1ΘG2。 (6) 输出信号y(n)为 y(n)=(Eoc+Eco)/2。 (7) 滤波器组合形式为 ψoc[f(n)]=max(Ocg1,Ocg2), (8) ψco[f(n)]=min(Oog1,Oog2), (9) 式中:Ocgi=(f°gi•gi)(n);Oogi=(f•gi°gi)(n);i=1,2。 滤波器的输出采用平均形式, y(n)=(ψoc+ψco)/2。 (10) 改进型形态滤波器与传统的形态滤波器相比,采用不同尺寸的结构元素,再滤除信号正负噪声的同时,能减小统计偏移现象[6]。 为了说明小波变换和数学形态学滤除噪声的有效性,构造一含噪声的仿真信号 s(t)=[1+cos (8πt)]sin (30πt)+ sin (70πt)+r(t)+η(t)。 (11) 它包含了一个调制波和一个正弦信号,r(t)为Gauss白噪声,η(t)为脉冲噪声。 图1a是没有加入噪声r(t)和η(t)的仿真信号;图1b是加入了2种噪声后的仿真信号;图1c是对含噪信号图1b进行小波去噪后的波形图;图1d是对图1c中的信号再进行数学形态学滤波后的波形图。从图1c中可以看出,采样点200,400,600及800处的脉冲噪声没有得到有效滤除,即小波变换虽然抑制了白噪声,但不能有效地抑制脉冲噪声。从图1d中可以看出,采样点200,400,600及800处的脉冲噪声得到了有效地抑制。表1为采用不同方式消噪的信噪比比较结果。 图1 仿真信号和消噪后的信号 表1 信噪比比较 由表1可知,信号在进行数学形态学滤波之前先进行小波消噪,可以提高信噪比。 在对信号进行数学形态学滤波之前先进行小波消噪,可以在有效消除信号干扰噪声的同时保留信号的特征。 HHT过程包括2个步骤[7]:第1步是将原始信号通过经验模式分解(EMD),分解成1组平稳化的数据序列集,即经验模态函数 (IMF)。第2步是将每个IMF函数与其HHT变换构成一个解析复函数,给出被分析信号的Hilbert谱。 每个IMF函数需满足2个条件[8]: (1)在整个序列上极值点的个数和零点的个数相等或相差1;(2)极大值和极小值所构成的上下包络线关于时间轴对称。 经验模式分解的过程主要包括下面几步。 (1)首先找到信号x(t)的局部最大值和最小值包络线,计算2条包络线的均值,得到一条均值曲线m1(t)。再求信号波形x(t)与该均值曲线的差,即 h1(t)=x(t)-m1(t) , (12) h1(t)即为第一阶IMF分量。 (2)把h1(t)当作原信号,根据类似(1)的做法,可得 h11(t)=h1(t)-m11(t)。 (13) c1(t)=h1k(t) 。 (14) (3)从原信号中减去c1(t),可得 r1(t)=x(t)-c1(t)。 (15) 对r1(t)重复步骤(1)和(2),可以得到第2个IMF。如果所得到的cn(t)或rn(t)小于给定的某一值,或成为一条单调曲线,则停止筛选。否则继续对得到的IMF进行类似步骤(3)的操作,得到所需要的一系列IMF。最终,原始信号可分解为 (16) 对每个IMF作HHT变换 (17) x(t)和y(t)组成解析信号z(t),即 z(t)=x(t)+jy(t)=a(t)exp[jθ(t)], (18) x(t)]。 (19) 原信号的Hilbert谱可以表示为 二维边际谱可表示为 (21) 本试验采用的轴承型号为6205-2RS,采样频率fs=12 kHz,轴承基本参数为:钢球个数Z=9,钢球直径Dw=7.938 mm,球组节圆直径Dpw=40 mm,接触角α=0°。 在试验台上测得一组外圈有损伤的轴承加速度信号,其主轴转速为1 796 r/min,轴转动频率为fr=29.9 Hz;外圈故障特征频率fe=107.8 Hz。 图2a是外圈故障信号的时域波形,图2b是外圈故障信号小波消噪后再进行数学形态学滤波的时域波形。对图2b中的信号进行EMD分解,再进行HHT变换得到的HHT边际谱图为图3。可以看出,HHT边际谱在外圈故障特征频率附近有明显的谱线,由此可以判断该滚动轴承的故障类型。 图2 外圈故障信号和消噪后的信号 在同一试验台上另外测得一组内圈有损伤的轴承加速度信号,主轴转速为1 733 r/min,轴承旋转频率fr=28.9 Hz,内圈故障特征频率fi=155.9 Hz。 图4a是轴承内圈故障信号的时域波形,图4b是内圈故障信号消噪后的时域波形。对图4b进行HHT变换得到的Hilbert边际谱图为图5。图5在内圈故障特征频率附近出现了明显的谱线,由此可得出该轴承在内圈沟道局部有故障缺陷。 图3 外圈故障信号的Hilbert边际谱图 图4 内圈故障信号和消噪后的信号 图5 内圈故障信号的Hilbert边际谱图 仿真和示例表明,对于机械信号,先进行小波消噪,再进行形态滤波和HHT分析,可以有效地消除信号干扰噪声,提取故障特征频率,实现对机械故障的诊断。 形态滤波作为一种自适应滤波方法,可以对机械信号进行故障诊断预处理。振动信号的仿真试验说明,在对信号进行形态滤波之前先进行小波消噪,可以更好地抑制白噪声和脉冲噪声,提高信噪比。将形态滤波和HHT相结合,用于滚动轴承故障诊断,结果表明该方法在故障信号含噪情况下可以较好地提取信号故障频率,达到故障诊断的目的。1.2 改进型形态滤波器
1.3 仿真试验

2 HHT变换
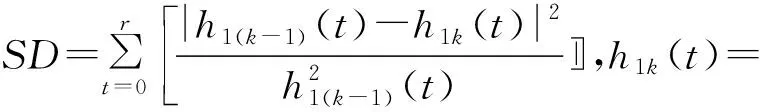
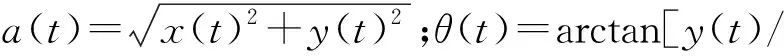

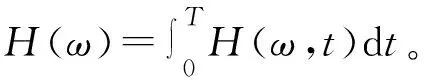
3 故障诊断示例
3.1 外圈故障诊断
3.2 内圈故障诊断
4 结束语
