一种巨磁阻传感器温度补偿方法
2011-07-26王小秋付敬奇
王小秋 付敬奇
(上海大学机电工程与自动化学院,上海 200072)
0 引言
随着1988年阿尔贝·费尔发现一种全新的物理现象——巨磁电阻效应,利用巨磁阻效应的巨磁阻传感器(giant magneto-resistive sensor,GMRS)不断被研制成功,它的出现使磁阻传感器、霍尔器件[1]、半导体磁敏电阻和磁敏二极管、三极管等传统的磁性传感器面临严峻的挑战。GMRS具有灵敏度高、体积小、探测范围宽、抗恶劣环境等优点,它已在自动化技术、卫星定位、导航、汽车工业、家用电器、医疗等领域获得广泛应用。但GMRS对环境温度变化敏感,对于高精度的测量,必须进行温度补偿[2]。
目前,常用的补偿方法主要有硬件补偿和软件补偿两大类。硬件电路补偿方法存在通用性差、调试困难、精度低等缺点,软件补偿能克服上述缺点,因此得到越来越多的重视[3]。
本文分析了NVE公司AAH002-02巨磁阻传感器的工作原理,并针对其温度特性进行了相应的试验,采用微粒群优化(particl swarm optimal,PSO)算法和二次最小二乘法对巨磁阻传感器进行了温度补偿,取得了较好的效果。
1 巨磁阻传感器测量原理
AAH002-02巨磁阻元件利用磁场变化引起阻值的变化来实现磁场的测量[4]。AAH002-02具有灵敏度高、体积小和功耗低等特点,采用惠斯通电桥模拟输出,适用于低磁场测量。巨磁阻调理电路采用仪表放大器INA118,它具有精度高、功耗低、共模抑制比高和工作频带宽等优点,适合对各种微小信号进行放大。巨磁阻传感器电路原理图如图1所示。

图1 巨磁阻传感器电路图Fig.1 Circuitry of GMRS
图1中,可调电位器RG实现仪表放大器放大系数调节。RG由下式决定:

式中:RG为调节电阻,kΩ;k为放大系数。巨磁阻传感器电阻变化与其受到的磁场大小成正比,即:

式中:S为传感器灵敏度;H为被测磁场。经过调理后可得传感器输出为:

式中:Vb为激励电压(本文取10 V)。
2 传感器温度特性试验
巨磁阻传感器温度特性试验采用日本爱斯佩克公司的SET-Z-041L型调温试验箱进行测试。该调温箱温度范围为-40~+150℃;温湿度波动度:高温≤0.5 K、低温≤1 K;温度均匀性≤2 K。在激励电压10 V的条件下,在-40~+80℃温度范围内传感器温度特性试验数据如表1所示。

表1 温度特性试验数据Tab.1 Test data of temperature characteristic
由表1试验数据可见,传感器零点温度特性为负温度特性,且表现为较为严重的非线性,采用常规的温度补偿方法难以实现其温度特性的良好补偿。
3 微粒群算法
3.1 算法原理
微粒群算法(PSO)是由Kennedy和Eberhart等人于1995年开发的一种演化计算技术[5],其基本思想来源于对鸟群简化社会模型的研究和行为模拟,是一种基于迭代模式的优化算法。微粒群算法的数学描述如下。
设微粒群体规模为N,其中每个微粒在D维空间中的坐标位置可表示为 Xi=(Xi1,Xi2,…,Xid,…,XiD),微粒i(i=1,2,…,N)的速度定义为每次迭代中微粒移动的距离,用 Vi=(Vi1,Vi2,…,Vid,…,ViD)来表示。微粒i在第d(d=1,2,…,D)维子空间中的飞行速度Vid根据下式进行调整:

式中:Pgd为整个微粒群的历史最优位置记录;Pid为当前微粒的历史最优位置记录;w为惯性权重;C1、C2为加速度常数;rand1、rand2为介于[0,1]之间的随机数;Vid为速度分量;Vmax为微粒的最大速度。
3.2 算法流程
基于微粒群算法流程图如图2所示。
本题是培养学生转化能力的极佳素材,虽然条件一读就懂、图形一看就明,但一做却又难以入手.不过,借助“知识溯源式目标分析法”却可巧妙地让解题思维转化路线图水落石出.
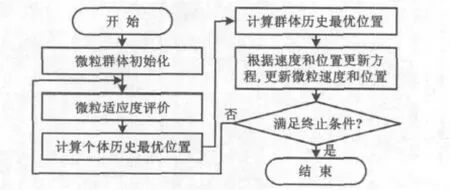
图2 微粒群算法流程图Fig.2 Flowchart of PSO algorithm
微粒群算法步骤如下。
①初始化一群微粒(群体规模为50),包括随机位置和速度;
②评价每个微粒的适应度;
③对每个微粒,将其适应值与其经历过的最好位置作比较,如果较好,则将其作为当前的最好位置Pid;
④对每个微粒,将其适应值与全局所经历过的最好位置作比较,如果较好,则重新设置Pgd;
⑤根据式(4)变化微粒的速度和位置;
⑥如未达到结束条件,则返回步骤②。
3.3 算法参数
①最大速度Vmax
Vmax决定当前位置与最好位置之间的区域分辨率(或精度)。如果Vmax太高,微粒可能会飞过最优解;如果Vmax太小,微粒不能在局部好区间之外进行足够的探索,导致陷入局部优值。对Vmax进行限制有3个目的:防止计算溢出、实现人工学习和态度转变、决定问题空间搜索的粒度。本文最大速度Vmax取5000。
②权重因子
PSO算法中有惯性权重w、加速常数C1和C2这3个权重因子。惯性权重w使微粒保持运动惯性,使其有扩展搜索空间的趋势,有能力探索新的区域。加速常数C1和C2代表将每个微粒推向Pbest和Gbest位置的统计加速项的权重,权重值低则允许微粒在被拉回之前可以在目标区域外徘徊,而权重值高时则会导致微粒突然冲向或越过目标区域。本文惯性权重w取0.8,加速常数 C1和C2取2,群体规模取50,最大迭代数Gmax取 2000。
4 温度补偿
本文采用微粒群二次拟合方法对巨磁阻传感器进行温度补偿。微粒群算法二次拟合得出传感器温度特性V(t)表达式为:
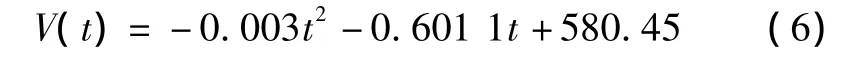
采用最小二乘法二次拟合得出的表达式为[7]:
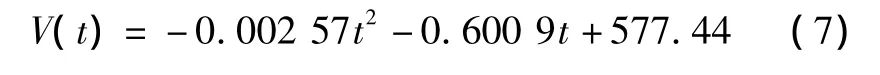
采用最小二乘法三次拟合得出的表达式为:
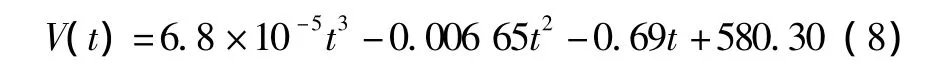
由计算得到的微粒群算法和最小二乘法温度补偿结果如表2所示。表2中,ΔV为传感器补偿前后输出偏差。

表2 温度补偿结果Tab.2 Results of temperature compensation
分析表2数据可知,巨磁阻传感器采用微粒群算法温度补偿后随温度的变化最大改变量为4.8 mV,满量程时相对误差为0.13%;而采用二次最小二乘法温度补偿后随温度的变化最大改变量为7 mV,满量程时相对误差为0.18%;采用三次最小二乘法温度补偿后随温度的变化最大改变量为5.4mV,满量程时相对误差为0.14%。由此可见,经过微粒群算法和最小二乘法温度补偿后,传感器满量程相对误差提高了一个数量级。相比于最小二乘法,采用二次拟合微粒群算法的满量程相对误差低于三次最小二乘拟合,其补偿效果更好,更适合于巨磁阻传感器温度补偿。
5 结束语
本文通过对巨磁阻传感器的特性及其工作原理的分析和研究,运用微粒群算法和最小二乘法对GMRS进行温度补偿,降低了传感器温度误差,提高了测量精度。温度补偿结果表明,微粒群算法比最小二乘法具有更好温度的补偿效果,但其也存在计算步骤复杂且优化时间长等问题。
[1]张珂,杨其华,李冰,等.基于霍尔器件的非接触式角度传感器研制[J].传感技术学报,2008,21(6):981 -984.
[2]辛守乔,邱清泉,张国民,等.线性双极巨磁阻传感器输出特性的测试研究[J].高压电技术,2009,35(10):2452 -2457.
[3]张艳锋,严家明.基于最小二乘法的压力传感器温度补偿算法[J].计算机测量与控制,2007,15(12):1870 -1871.
[4]陈晓晖.基于GMR磁传感器芯片的弱磁探伤电路[J].科技资讯,2006(20):211 -212.
[5]Tang Jun,Zhao Xiaojuan.An enhanced opposition based particle swarm optimization[C]∥2009 Global Congress on Intelligent Systems(GCIS 2009),Xiamen,2009:149 -153.
[6]江维,沈斌,胡中功.微粒群算法参数的理论分析[J].化工自动化与仪表,2009,36(4):38 -40.
[7]黄开志,黄耀,雍毅.一种基于示值误差的传感器标定方法[J].传感器与微系统,2009,28(3):104-107.
