基于二维主分量分析的人耳身份识别研究
2011-07-25唐邦杰
唐邦杰, 封 筠
(石家庄铁道大学信息科学与技术学院,河北石家庄050043)
0 引言
作为一种被逐渐关注的生物识别特征体,人耳具有稳定性,独特性和较高的用户可接受性等优点。人耳识别技术的研究与探索,将对生物特征识别技术的发展起到推动和促进作用,具有很高的理论研究与应用价值。在人耳特征提取的研究中,Victor等将在人脸识别中较流行的标准主分量分析(Principal Component Analysis,PCA)方法应用于人耳识别,得到特征耳,并将人耳识别性能与人脸识别性能进行对比[1];Burge和Burger提出了使用Voronoi图表的邻接图匹配方法[2];Hurley等模仿自然界的电磁力场过程,提出了一种基于力场转换理论方法的人耳识别[3];Michal提出了一种几何学的提取人耳轮廓质心特征点的人耳识别方法[4];穆志纯等提出了基于长轴的形状特征提取方法[5];封筠等提出了一种基于局部二值模式与核Fisher判别分析的人耳识别方案[6];梁晓霞等提出了一种基于Gabor变换和灰度梯度共生矩阵的人耳身份识别方法[7];Hui Chen等使用距离传感器直接获取人耳3D图像数据,提出基于3D人耳检测识别方法[8]。
Kirby M等人早在1990年就将主分量分析应用于人脸识别[9],Turk M和Pentland A在Kirby的基础上将主分量分析发展成特征脸(Eigenface)算法用于人脸识别[10]。传统的PCA方法虽然能够将数据特征降维,但是需要将每个图像样本按像素转化为一维向量。对尺寸为的图像,其协方差矩阵的维数为,随着图像尺寸的增大,所需要的计算量飞速增加。如果训练样本数目很少,导致计算所得的特征向量不够准确和稳定。因此,为了更稳定地提取特征并减少运算量,Yang J,Zhang D等人对传统PCA方法进行推广,提出了2-D主分量分析(2D principal component analysis,2D-PCA)[11]的方法。本文将基于二维图像矩阵的2D-PCA方法应用于人耳识别,直接对2D图像矩阵进行特征提取,避免了庞大的计算量。
1 一维主分量分析
主分量分析(又称K-L变换),是一种基于目标二阶统计特征的最佳正交变换,因为经过变换后产生的新的分量相互正交且不相关,且用部分新的分量对原样本重构以后与原样本的均方误差最小。这些都决定了它在特征提取和数据压缩方面的重要地位。可以证明,在数学上,PCA可以通过求解特征值问题来求得用于样本的投影向量。
设x是一个n维随机向量,对一组数据{xi|i=1,2,…,N},将其表达为矩阵形式X=[x1,…,xn]对X的所有列取平均得到

式中,N表示样本的总个数;μ是所有样本的均值。
令¯X=[μ,μ,…,μ]。数据X对应的协方差矩阵

设St的秩为m,而λ1,λ2,…,λm是矩阵St的特征值,特征值按从大到小排序:λ1>λ2>…>λm。ωi,i=1,2,…,m是对应特征向量。则λi与ωi满足

令λi代表第i个特征值,则第i个主元素的贡献率为

前r个主分量的累计贡献率为

贡献率表示所定义的主分量在整个数据分析中所占比重,取前r个主分量来代替全部变量,累计贡献率的大小反映了其可靠性。令W=[ω1,ω2,…,ωr],在主分量分析中,ωi为这组数据的主分量,W为这组数据的主分量矩阵。
2 二维主分量分析
二维主分量分析(Two Dimensional Principal Component Analysis,2D-PCA)方法利用2D图像矩阵直接构造协方差矩阵,进而求出协方差矩阵的主分量特征向量,然后将测试2D图像直接向最优投影方向上投影以获得图像的特征表示。2D-PCA不同于PCA,可以直接在2-D图像矩阵上进行处理,而不需要先将图像矩阵转化为一维向量,避免了庞大的求取特征值的计算。
设x表示n维列向量,图像A看作m×n的矩阵,通过如下线性变换

将图像A投影到向量x上,得到一个m维的列向量y,成为图像A的投影特征向量。向量x称为投影向量。
使用投影后训练样本总体散度作为准则函数J(x)来衡量投影向量x的优劣。

式中,Sx表示投影特征向量的协方差矩阵,tr Sx表示Sx的迹。
定义图像散度矩阵

易知Gt是一个n×n的非负定矩阵,可以用训练样本图像直接估计。设总共K幅训练样本图像,第i幅图像用m×n的矩阵Ai(i=1,2,…,K)来表示,训练样本均值图像为

估计图像协方差矩阵


通过最大化准则函数J(x)来寻找一个最优的投影方向x,使得所有训练样本投影后,达到总体散度最大化的效果。选择相互正交且极大化准则函数的一组投影向量
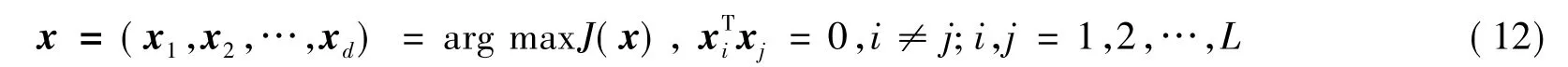
这里投影向量x1,x2,…,xL就是图像协方差矩阵的前L个最大特征值λ1,λ2,…,λL所对应的特征向量(λ1≥λ2≥…≥λL>0)。
3 人耳身份识别
3.1 USTB人耳图像库
实验数据来自北京科技大学USTB人耳图像库1、库2和库3[12]。
库1中包括59人,每人3幅右耳图像,分别是正面一幅、轻微变化角度一幅、光照变化一幅,连续3幅为同一人的人耳图像,依次排列。
库2中包括77人,每人4幅右耳图像,分别是正面1张、角度变化2张、光照变化1张,第一幅图像与第四幅图像均为人耳的正面图像,但光照条件变化较大,第二幅图像和第三幅图像与第一幅图像光照条件相同,但分别相对于第一幅图像旋转+30°和-30°,连续4幅为同一人的人耳图像,依次排列。
人生是一段不断追求和完善的旅程,无数智者不停地付出,为的是拥有一个完美的人生,但完美难求。正是因为完美难求,才有了拼搏与奋斗的心境,才能够在永不懈怠的付出中,让人生一步一步跨越障碍,走向迢遥,走向辉煌。
库3中包括79人,每人10幅正常人耳图像,分别拍摄正侧面,向右转5°,10°,15°,20°共5种角度,每种角度2幅图像。连续10幅为同一人的人耳图像,依次排列。人耳库部分图像示例由图1所示,每幅子图取3人为例,每一行为同一人的不同变化时人耳图像。
3.2 识别流程
人耳识别属于典型的模式识别问题,本识别方案主要由三部分构成,即人耳图像预处理,人耳图像特征提取,最近邻分类器(Nearest Neighbor Classifier,NNC)。系统结构如图2所示。
实验针对人耳图像先使用维纳滤波进行去噪和修复,然后通过直方图均衡化方法进行图像对比度增强,并减少不同图像之间的光照差异,最后采用双三次插值法将人耳图像归一化为62×40像素。
实验分别针对USTB人耳图像库1、库2和库3采用PCA、2D-PCA方法提取图像特征,在不同相似性测度下,研究了不同方法中特征维数或贡献率变化时,对识别性能的影响。实验采用最近邻分类器对测试样本进行分类,其基本原则是取未知样本x的最近邻,其属于哪一类就将x归为哪一类。由于不同的相似性测度具有其各自的适用范围及优缺点,实验中主要比较了如下三种相似性测度,以便找出更适用于人耳识别的测度。
(1)欧氏距离
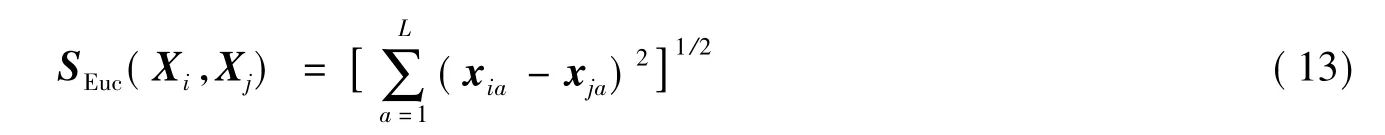
(2)明氏距离

(3)马氏距离
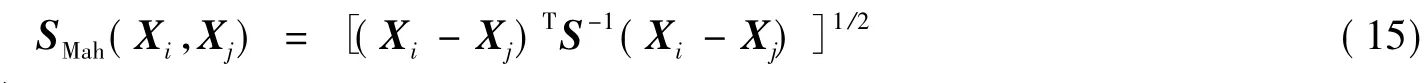
式中,S为样本的协方差矩阵。
4 实验结果与分析
实验中首先分析了采用不同特征提取方法时识别性能与特征维数的关系,交叉验证的具体方案如下:

图1 USTB人耳库部分图像示例

图2 人耳识别系统流程
(1)对库1中人耳图像采用3折交叉验证,即取每人2幅图像作为训练样本,其余1幅为测试样本,求得3种不同组合的平均识别率。
(2)对库2中人耳图像采用4折交叉验证,即取每人3幅图像作为训练样本,其余1幅为测试样本,求得4种不同组合的平均识别率。
(3)对库3中人耳图像采用10折交叉验证,即取每人9幅图像作为训练样本,其余1幅为测试样本,求得10种不同组合的平均识别率。
4.1 基于一维主分量分析的人耳识别实验结果
图3显示了在三种相似性测度下,不同人耳图像库中PCA方法的识别率随贡献率变化的关系曲线。在贡献率取90%~100%时取得了最好的识别效果。
4.2 基于二维主分量分析的人耳识别实验结果
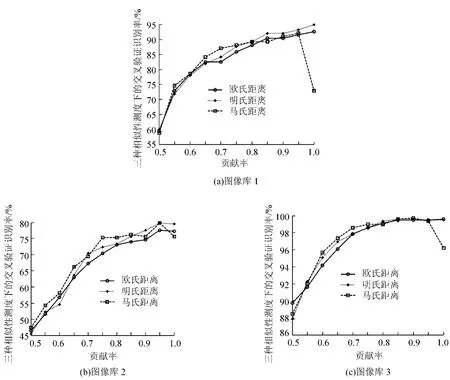
图3 采用PCA方法时识别率随贡献率变化的关系曲线
图4分别显示了分别在欧氏距离与明氏距离测度下,不同人耳图像库中2D-PCA方法的识别率随特征维数变化的关系曲线。在各个相似性测度下,识别率走向大体相同,且对不同的图像库在特征维数取4维或5维时取得了最好的识别性能。
4.3 欧氏距离测度下的人耳识别性能对比
通过上面实验可获得针对不同方法达到最高识别率时的特征维数。下面重点选取欧氏距离测度,研究分析了PCA与2D-PCA两种特征提取方法在不同折数的交叉验证中的性能比较。具体交叉验证方案如下:
(1)对库1中人耳图像采用3折交叉验证(取每人2幅图像作为训练样本,其余1幅为测试样本,求得3种不同组合的平均识别率)。
(2)对库2中人耳图像分别采用4折交叉验证(取每人3幅图像作为训练样本,其余1幅为测试样本,求得4种不同组合的平均识别率)和2折交叉验证(取每人2幅图像作为训练样本,其余2幅为测试样本,求得6种不同组合的平均识别率)。
(3)对库3中人耳图像分别采用2折交叉验证(取每人5幅图像作为训练样本,其余5幅为测试样本,求得252种不同组合的平均识别率)、5折交叉验证(取每人8幅图像作为训练样本,其余2幅为测试样本,求得45种不同组合的平均识别率)和10折交叉验证(取每人9幅图像作为训练样本,其余1幅为测试样本,求得10种不同组合的平均识别率)。实验数据如表1所示。
4.4 实验结果分析
(1)图3与图4结果比较分析。由图3与图4可知,两种特征提取方法获得最高识别率时的具体数据为:
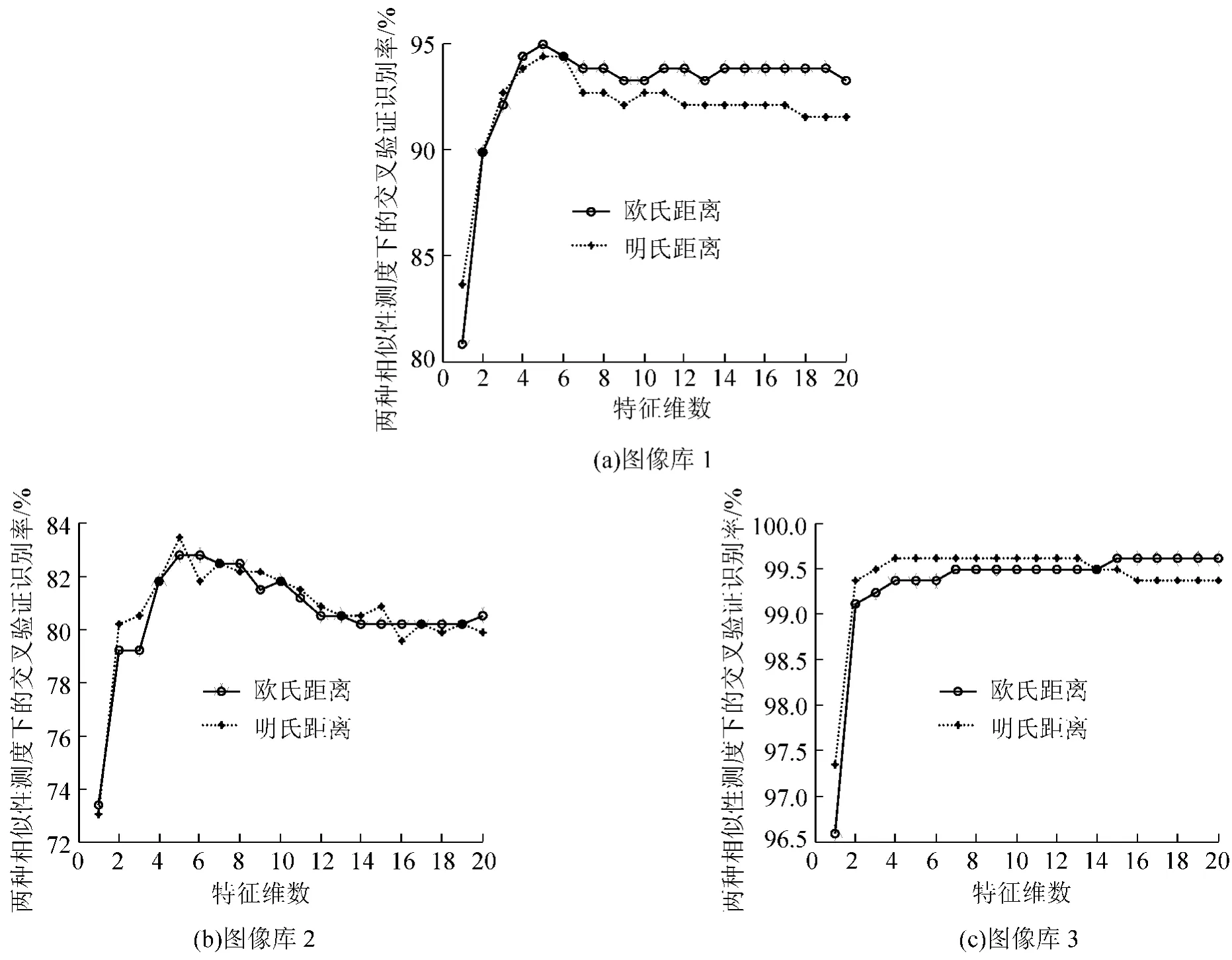
图4 采用2D-PCA方法时识别率随特征维数变化的关系曲线

表1 欧氏距离测度下的人耳识别数据
库1中,PCA方法在明氏距离测度下,贡献率取100%时,识别率为94.92%;2D-PCA方法在欧氏距离测度下,特征维数取5维时,识别率为94.92%。
库2中,PCA方法在明氏距离与马氏距离测度下,贡献率取95%时,识别率为79.87%;2D-PCA方法在明氏距离测度下,特征维数取5维时,识别率为83.44%。
库3中,PCA方法在马氏距离测度下,贡献率取90%时,识别率为99.62%;2D-PCA方法在明氏距离测度下,特征维数取4维时,识别率为99.62%。
通过对比图3与图4可知,无论在何种相似性测度下,2D-PCA方法的识别率均不低于PCA方法的识别率。除此之外,在PCA方法的起始贡献率为50%的情况下,三个库中2D-PCA的最低识别率均高出PCA的最低识别率约9%~28%。
综合三个人耳图像库的识别率曲线走向,PCA方法中,识别率随着贡献率的增加呈现升高的趋势。但随着贡献率的变化,识别率波动较明显,最低识别率与最高识别率之间的差异较大。所有相似性测度下,在贡献率取90%~100%时取得了最好的识别效果。2D-PCA方法中,库1和库2的所有相似性测度下以及库3的明氏距离测度下,识别率在特征维数选取4维或5维时,取得了最好的识别效果。随着特征维数的继续增加,识别率逐渐降低。库3在欧氏距离测度下,特征维数取15维时,识别率最高。2D-PCA方法在所有特征维数下识别率始终保持在较高水平上,且波动相对较小。由此可见,基于2D图像的方法相较于一维图像的方法更具有稳定性和鲁棒性。
(2)表1数据结果分析。由表1不难发现,随着交叉验证折数的增大,每个图像库的整体识别率都有增加的趋势。同时,库3的识别效果显著高于库1和库2,库2的识别效果相对较差。库1中,两种方法最低识别率为92.66%,最高为94.92%;库2中,两种方法最低识别率为68.61%,最高为82.79%;库3中,两种方法的识别率介于97.88%到99.62%之间。在每个库的不同交叉验证中,2D-PCA的平均识别率均不低于PCA,在库1和库2上识别率差异体现较明显,在库3的五折和十折交叉验证中,2D-PCA和PCA的识别率均达到了99.48%以上。这验证了这两种特征提取方法在人耳识别研究中的有效性。
训练时间上,由于2D-PCA克服了将二维图像矩阵转换成一维图像向量后造成高维运算的缺点,所以单张图片PCA的训练时间约是2D-PCA的1.55到2.34倍。
(3)综合图3、图4和表1中的数据,2D-PCA方法的训练时间更低,识别率更高,且在特征维数较少时,2D-PCA方法仍然能够获得较好识别效果,总体波动相对较小。因此,无论从时间复杂度,还是从识别效果上看,都可以得出基于图像矩阵的2D-PCA方法优于基于一维图像向量的PCA方法的结论。
5 结论
将基于二维图像的2D-PCA方法用于人耳识别,与传统的一维线性子空间PCA方法在不同相似性测度、不同特征维数下进行对比仿真交叉验证实验,采用最近邻分类器对特征进行分类。综合时间复杂度和识别效果来看,针对三个不同人耳图像库的实验结果验证了基于图像矩阵的2D-PCA方法优于基于一维图像向量的PCA方法,是一种执行效率更高,鲁棒性更强的有效人耳识别方法。本文工作进一步表明2D-PCA方法不仅可成功应用于人脸识别等领域,而且在人耳图像特征提取中同样具有深入的研究价值。
[1]Victor B,Bowyer K W,Sarkar S.An evaluation of face and ear biometrics[C]//Proceedings of International,Conference on Pattern Recognition.Quebec:IEEE Press,2003:429-432.
[2]Burge M,Burger W.Ear biometrics in computer vision[C]//Proceedings of the 15th International Conference of Pattern Recognition.Barcelona:IEEE Press,2000:822-826.
[3]Hurley D J,Nixon M S,Carter J N.Force field energy functionals for ear biometrics[J].Computer Vision and Image Understanding,2005,98(3):491-512.
[4]Michal,Choras.Ear biometrics based on geometrical feature extraction[J].Electronic Letters on Computer Vision and Image A-nalysis,2005,12(5):84-95.
[5]Mu Zhichun,Yuan Li,Xu Zhengguang.Shape and structural feature based ear recognition[C]//Proceedings of the 5th Chinese Conference on Biometric Recognition,SINOBIOMETRICS.Guangzhou:Springer Press,2004:633-670.
[6]Feng Jun,Mu Zhichun,Duan Shufeng,et al.Ear recognition based on local binary pattern and kernel Fisher discriminant analysis[J].Journal of Information and Computational Science,2008,5(2):887-894.
[7]梁晓霞,封筠.基于Gabor变换和灰度梯度共生矩阵的人耳识别研究[J].石家庄铁道大学学报:自然科学版,2011,24(1):78-83.
[8]Hui Chen,Bhanu B.Contour matching for 3D ear recognition[C]//Seventh IEEE Workshops on Application on Computer Vision.Breckenridge,CO:IEEE Press,2005:123-128.
[9]Kirby M,SIrovich L.Application of the Karhunen-Loeve procedure for the characterization of human faces[J].IEEETrans.PAMI,1990,12(1):120-108.
[10]Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.
[11]Yang J,Zhang D,Frangi A F,et al.Two-dimensional PCA:A new approach to appearance-based face representation and recognition[J].IEEE Trans.PAMI,2004,26(1):131-137.
[12]穆志纯.北京科技大学人耳识别实验室——开放式人耳图像库[EB/OL].(2009-01-18)[2011-11-1].http://www.ustb.edu.cn/resb/subject/subject.htm.
