局域均值分解法在轴承故障诊断中的应用
2011-07-25于雯陈晓平王禄
于雯,陈晓平,王禄
(江苏大学 电气与信息工程学院,江苏 镇江 212013)
在工程中测取的滚动轴承故障信号一般是非平稳、非线性的,目前对此类信号进行特征提取常用的方法有经验模式分解方法和小波分解方法[1]。经验模式分解方法存在过包络、欠包络和端点效应现象,以及在利用Hilbert变换形成解析信号后计算瞬时频率时会产生无法解释的负频率等问题;小波分解方法中的小波基选择对分析结果影响较大,在整个分析过程中都无法更换,因此小波变换对信号的处理缺乏自适应性。
2005年文献[2]提出了一种新的自适应时频分析方法——局部均值分解(Local mean decomposition, LMD)方法。通过LMD可将复杂的多分量信号直接分解为若干个乘积函数(production function, PF)的线性组合,其中每个PF由1个包络信号和1个等幅调频信号相乘得到,包络信号即该PF的瞬时幅值,包含信号调幅信息。等幅调频信号展开相位的导数即PF的IF,包含信号调频信息。LMD不需要通过Hilbert变换求解IF,避免了Hilbert变换加窗效应所带来的解调误差。由于不受Bedrosian定理和Nuttall定理的限制,因此不会出现负频率现象[3]。
1 局域均值分解法原理
LMD分解的结果是得到一系列的PF分量,其具体分解步骤如下:
mi=(ni+ni+1)/2,
(1)
ai=|ni-ni+1|/2。
(2)
(2)对mi和ai进行滑动平均,得到平滑的局域均值曲线m11(t)和局域包络曲线a11(t)。
(3)将m11(t)从原始信号x(t)中分离出来,并除以a11(t)得到调频信号
s11(t)=[x(t)-m11(t)]/a11(t)。
(3)
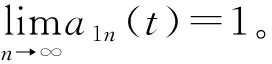
(5)将上述迭代过程中产生的所有局域包络函数相乘便可以得到第1个PF的包络信号,即

文章介绍轴系安装过程和轴系校中方法,通过测量分析轴系相邻法兰上的开口(曲折)值和偏移值对轴系安装和校中质量进行评估。实船应用证明:轴系安装和校中满足规范和设计要求。通过现场观察和分析总结,对直线校中法的具体工艺提出一些改进措施,以期进一步提高轴系安装与校中的质量。
(4)
由等幅调频信号s1n(t)求得瞬时频率
(5)
将a1(t)和s1n(t)相乘便可得到原始信号的第1个PF分量
P1(t)=a1(t)s1n(t)。
(6)
(6)将P1从x(t)中分离出来,得到一个新的信号u1(t),对u1(t)重复以上步骤,循环k次,直到uk(t)为常数或单调函数为止。将x(t)分解为k个PF分量和1个单调函数uk之和,即
(7)
式中:Pm为第m个PF分量,m=1,2,…,k;uk(t)为残余项;Pm(t)为包络信号和纯调频信号的乘积。这说明LMD分解后的原信号的信息保持良好,没有造成信息丢失。
2 仿真信号分析
构造一个仿真信号
x(t)=x1(t)+x2(t)=[1+0.5cos(14πt)]·cos(200πt+2sin(10πt)+1.5sin(30πt);
t[0,1],(8)
该信号时域波形如图1所示。
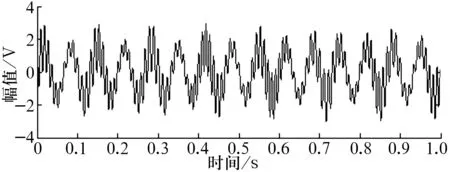
图1 构造信号的原始波形
对构造信号进行LMD分解,根据Simth的附录[2],滑动平均的跨度取最长相邻极值点距离的1/3。设原来序列为D(i),i=1,2,…,n,则滑动平均的公式为
(9)
式中:2N+1即为滑动跨度,滑动跨度必须为奇数,如果是偶数则减去1。在边界附近,减小跨度,以不超过序列的端点为限。如果在滑动平均之后,尚有相邻点的值相等,则再次做滑动平均,直到任何相邻点不相等。将信号的采样时间设为100 ms,采样后信号波形如图2所示,第1次平滑前后的波形如图3、图4所示。

图2 采样时间为100 ms时的原始信号波形

图3 第1次平滑前后的局域包络函数

图4 第1次平滑前后的局域均值函数
接着通过LMD分解得出信号的3个PF分量和1个残余量。波形如图5所示。由LMD信号的分解结果可知,PF1分量为调幅调频信号,对应着(8)式中的x1(t),PF2为正弦波的波形,对应着(8)式中的x2(t)。最先得到的PF1频率最高,PF2至PF3的频率逐渐降低,PF3及残余项的幅值都很小,对PF1分量的瞬时幅值和瞬时频率分别作快速Fourier变换(FFT),可以分别得到信号的调幅特征和调频特征[3]。PF1的瞬时幅值就是其包络信号,瞬时频率是采用直接法[4]求得的,即f(t)=φ(t),而φ(t)=arccos (s(t)),其中s(t)为纯调频信号,取值范围为-1≤s(t)≤1,由于上述求瞬时频率的方法简单直接,因此称之为直接法。直接法的优点是计算得到的瞬时频率都是正值,不会出现难以解释物理意义的负频率。

图5 构造信号的PF分解结果
如图6所示,图6a为PF1的瞬时幅值,图6b为其经过FFT变换后的频谱图,调制频率为7.3 Hz,与原信号基本一致。图6c为PF1的瞬时频率,图6d为其经过FFT变换后的频谱图,调制频率为4.88 Hz,与原信号基本一致。可见LMD分解是成功的。

图6 PF1的瞬时幅值和瞬时频率
3 LMD在轴承故障检测中的应用
试验在文献[5]的试验数据下进行。试验台由功率为1.47 kW的电动机、扭矩传感器/译码器、测力计和电气控制装置组成。轴承型号为6205-2RS,采样频率fs=12 kHz,点蚀故障点通过电火花机在轴承内、外圈沟道中央位置上加工微小凹坑来模拟,取2 048个点进行分析。轴承基本参数为:钢球直径Dw=7.938 mm,钢球数8个,球组节圆直径Dpw=40 mm,轴承接触角α=0°。用检测振动的压电式加速度传感器收集轴承运转时的振动数据。为得到轴承在不同方向上的振动信号,在轴承座上放置了2个传感器,位置如图7所示。测得主轴转速为1 750 r/min,轴转动频率fr=29.16 kHz;计算得外圈故障特征频率fe=104.57 Hz,内圈故障特征频率fi=157.94 Hz。

图7 传感器测试图
3.1 外圈故障分析
首先用小波包分解法对采集到的外圈故障信号进行消噪处理[6],图8a为外圈信号时域图, 图8b为消噪后的外圈信号时域图。

图8 外圈信号时域图及消噪后的时域图
然后利用LMD对消噪后的滚动轴承外圈故障信号进行分解,得到PF1,PF2,PF3分量及1个残余量。由于PF1分量具有比较明显的冲击特征,对PF1的瞬时幅值做FFT得到如图9所示的频谱图,从图上可以看出x轴坐标值为105.5 Hz附近出现了比较明显的谱线,与理论值(104.57 Hz)非常接近,而且在理论故障特征频率的2倍频处也出现了明显的谱线,由此可以说明滚动轴承外圈出现了故障,LMD分解方法是有效的。

图9 PF1分量瞬时幅值的频谱图
3.2 内圈故障分析
同理,对采集到的滚动轴承内圈故障信号用小波包分解法进行消噪处理,图10a为内圈信号时域图,图10b为消噪后的内圈信号时域图。

图10 内圈信号时域图及消噪后的时域图
然后利用LMD对消噪后的滚动轴承内圈故障信号进行分解,得到PF1,PF2,PF3分量及1个残余量。由于PF2分量具有比较明显的冲击特征,对PF2的瞬时幅值做FFT得到如图11所示的频谱图,从中可以看出在x轴坐标值为158.2 Hz附近出现了比较明显的谱线,与理论值(157.94 Hz)非常接近,而且在理论故障特征频率的2倍频处也出现了明显的谱线。除此之外,在图中x轴坐标值为58.59 Hz处也有比较明显的谱线,这与轴转动频率29.16 Hz的2倍频的理论值比较接近,由此可以说明滚动轴承内圈出现了故障。LMD分解方法是有效的。
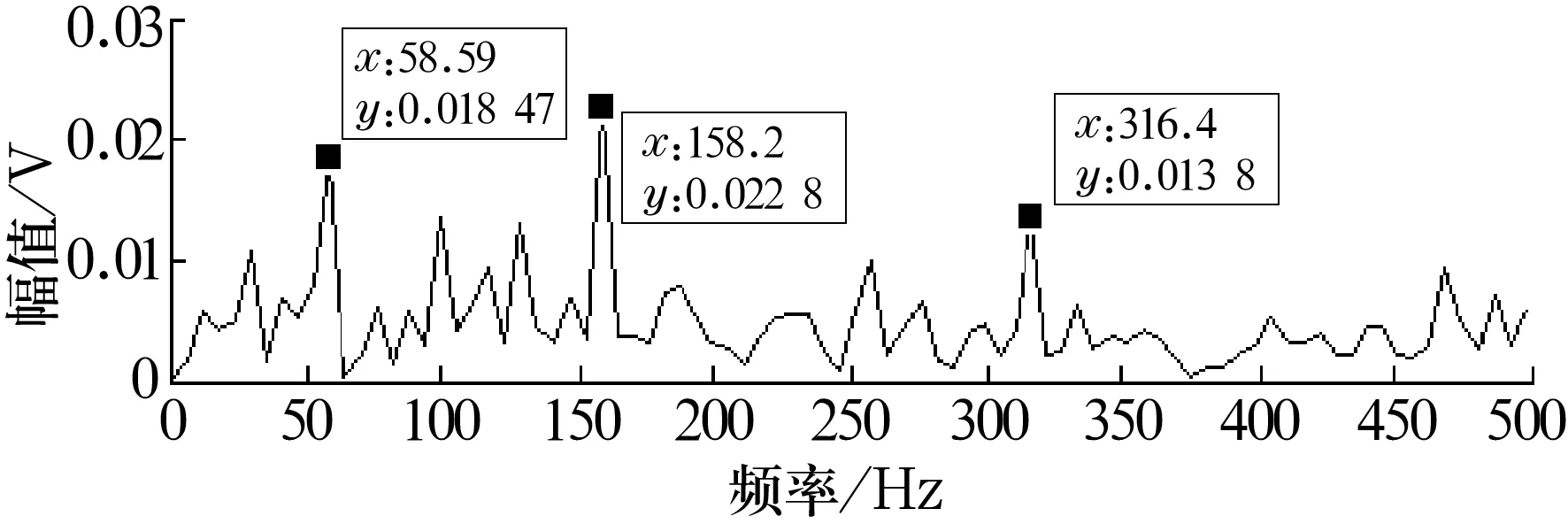
图11 PF2分量瞬时幅值的频谱图
4 结束语
通过构造一个仿真信号,用LMD方法将其分解为1个调频调幅信号和1个正弦信号,并成功地将分解出的调频调幅信号的瞬时频率和瞬时幅值分开分析,求出了调频调幅信号的调频特征和调幅特征,验证了LMD方法的有效性。并将LMD这种新方法引入到石油钻井平台滚动轴承的故障诊断中去,成功地分析出了故障特征。
但是LMD方法作为一种新的自适应时频分析方法,仍有许多理论问题,比如平滑次数、迭代终止条件、以及局域均值求解速度过慢等问题需要深入研究[7]。
