基于迭代形态梯度解调算子的轴承故障检测

陈彦龙，张培林，王怀光，李兵

(军械工程学院，石家庄 050003)

滚动轴承是旋转机械中最常见的零部件之一，其运行状态往往直接影响到设备的性能。当其发生故障时，往往在振动中包含某些突变信号，呈现出一定的非平稳性[1]，这是一种突发性强又很危险、早期症状较难识别的故障，此类故障的诊断一直是研究的热点[2-3]。故障诊断的关键是获取有效的故障特征信息，但通过传感器提取的轴承振动加速度信号具有非平稳特征，反映状态信息的能量也很微弱，给故障诊断带来了困难。

数学形态滤波基于信号的几何特征,利用预先定义的结构元素对信号进行匹配,以达到提取信号、保持细节和抑制噪声的目的。数学形态学已被广泛应用于边缘检测、图像分割、形状识别、图像恢复与重建等图像处理问题。同时它又具有非常有效的非线性滤波技术,对信号处理的效果只取决于待处理信号的局部形状特征,比传统的线性滤波更有效,因此已经应用在心电信号的处理中[4]。数学形态学在振动信号处理领域的研究还刚刚起步, 文献[5]提出采用单一结构元素的传统形态滤波器对信号进行降噪。文献[6]利用梯度解调算子对轴承进行故障冲击频率提取，可有效地对轴承故障状态进行准确的判断。

然而，梯度解调算子分析存在结构元素选择的问题，文献[6]即根据相关原则，采用扁平结构元素。若结构元素选择不当，将受到低频分量干扰导致解调效果不佳，此时梯度解调算子分析会将低频信号作为调制频率解出。

因此，提出了不需严格选择结构元素，从受到低频信号和噪声干扰信号中提取冲击特征的形态梯度迭代算法，通过仿真信号和实测轴承故障信号对提出的方法进行分析，并与形态梯度算子处理结果进行对比研究。结果表明，迭代形态梯度解调算法具有计算速度快，不受低频分量干扰，结果准确稳定的特点，为判断轴承故障状态提供了一种新方法。

1 数学形态学概述

数学形态学是以集合论、积分集合和拓朴学为基础发展起来的有别于时空域分析和频域分析的数学方法。其根据处理对象的形状特征，用特定的结构元素进行形态变换来达到信号处理的目的[7-8]。具有完整的理论、方法和算法体系，非常适合信号的几何形态分析和描述。

数学形态学的基本运算包括腐蚀和膨胀2种算子[9]。它们可以在保持信号基本特征的前提下，去除信号中尺度上小于结构元的细节，从而得到结构简化的信号数据。假设输入序列f(n)为定义在F={0，1，2，…，N-1}上的离散函数，定义序列结构元素g(m)为G={0，1，2，…，M-1}上的离散函数，且N≫M。

f(n)关于g(m)的腐蚀定义为

(1)

f(n)关于g(m)的膨胀定义为

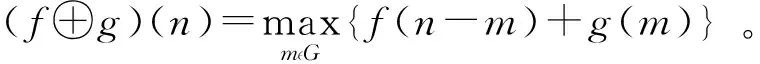
(2)

膨胀变换是一种扩张变换,它使目标肢体扩张,孔洞收缩；而腐蚀为收缩过程,使目标肢体收缩,孔洞扩张。等价于离散函数在滑动滤波窗(相当于结构元素)内的最小值和最大值滤波[10]。

膨胀和腐蚀通过不同的组合,就可形成丰富多彩的算法和信号处理系统。形态梯度为信号f(n)分别经过结构元素g(m)膨胀和腐蚀后的差分，其表达式为

GRAD(f)=f⊕g(n)-fΘg(n)。

(3)

在一维信号处理中，形态梯度算子用来检测加于稳态信号上的暂态信息，可以有效地检测出脉冲的位置，较好地保留脉冲的形状，是凸显脉冲信息的有力工具。但选择不同的结构元素，将引起结果的较大差异，观察发现，无论如何改变结构元素，对进行过形态梯度运算的信号再次进行形态梯度变化，将使处理后的信号在时域的统计特征量发生变化，并最终表现出稳定的变化规律。

基于形态梯度的上述特性，提出基于迭代的形态梯度解调算子，用于提取隐含在振动信号中的反映轴承故障信息的脉冲特征，将第n次进行形态梯度运算前后的信号时域统计特征量的变化作为是否进行第n+1次形态梯度运算的依据，实现对轴承故障的诊断。

2 仿真分析

设仿真信号为x(t)，进行试验分析，采样频率为2 048 Hz，采样时间为1 s。

x(t)=x0(t)+y+xn(t)，

(4)

式中：x0(t)为周期性脉冲衰减信号，每周期衰减函数为10e-6 000tcos (2 000πt)，频率为32 Hz；y为频率分别为30 Hz与50 Hz的正弦信号之和，幅值为10；xn(t)为Gauss白噪声。

图1为仿真信号的时域波形。由于噪声信号和低频信号的干扰，从时域图中不易观察出脉冲信号的周期特征。

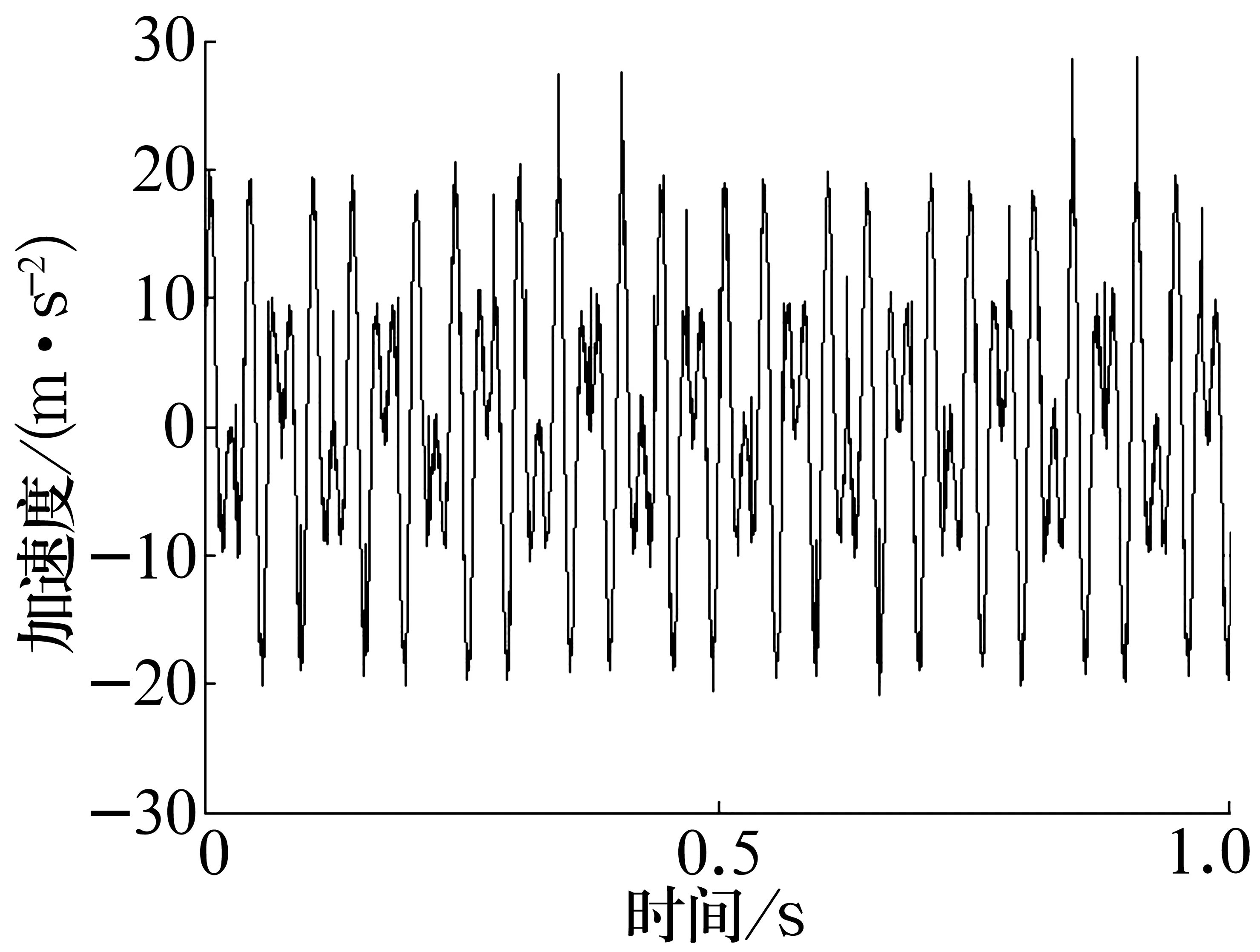
图1 仿真脉冲信号

任意选择结构元素 ，取[0 1 0；1 1 1；0 1 0]，图 2为形态学梯度算子滤波后的时域信号及其频谱。由于低频信号的干扰，形态梯度算子提取的信号中存在着明显的低频分量差值(20 Hz)，对信号分析造成干扰，无法准确判断故障原因，甚至引起误诊断。

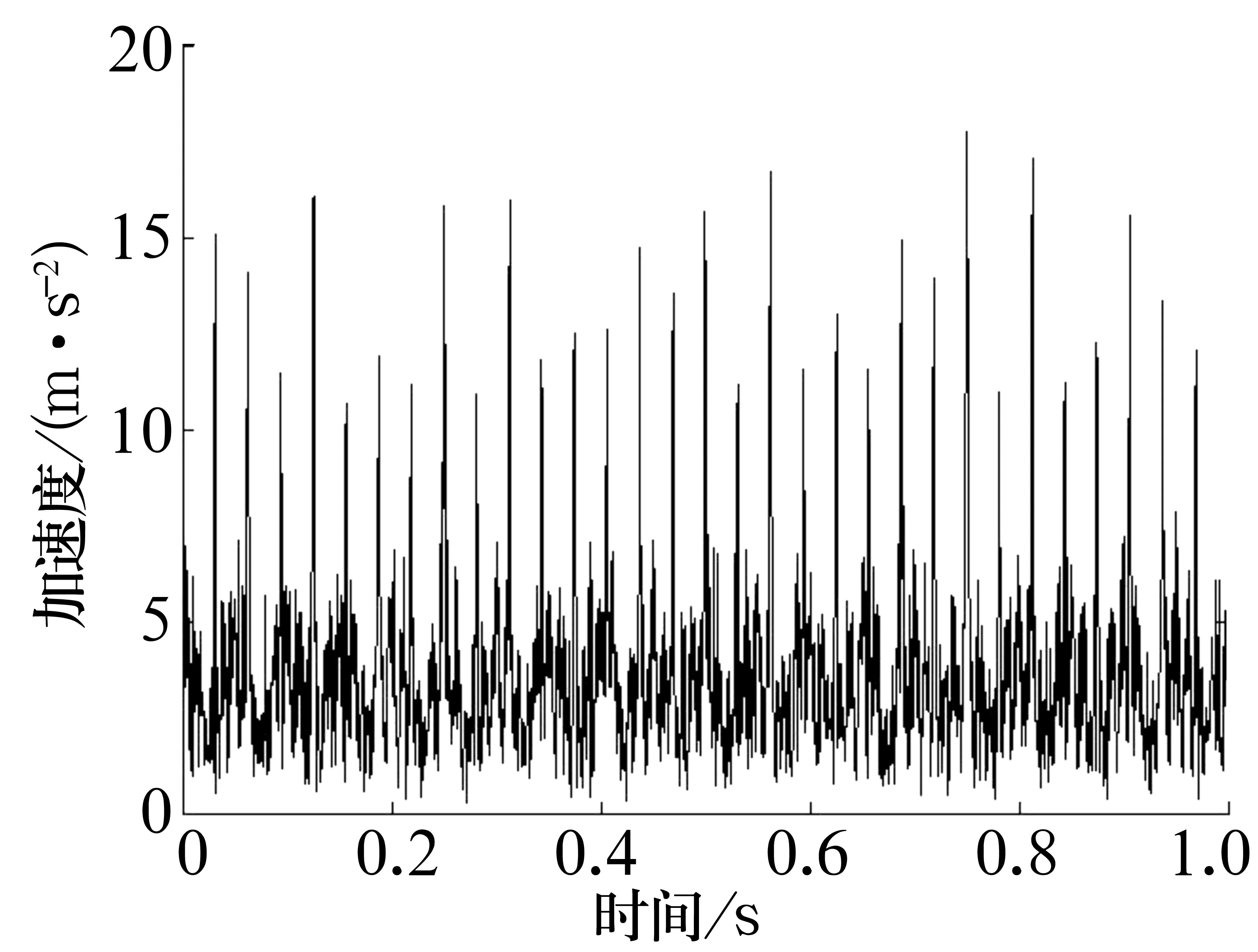
(a) 形态梯度算子解调信号

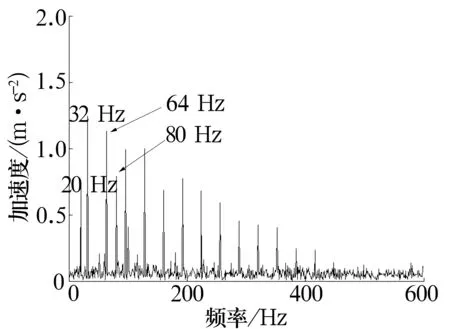
(b) 形态梯度算子解调信号频谱图2 形态梯度算子分析

图3为迭代形态梯度算子滤波后的时域信号及其频谱。从图2和图3可以看出，形态梯度算子和迭代梯度算子均能够提取出信号的脉冲信息。但迭代形态学梯度算法不受低频分量的干扰，可有效提取出脉冲信号，从图3b中几乎找不到低频分量频率，只有脉冲信号的特征频率，结果准确可靠。

(a) 迭代形态梯度算子解调信号

(b) 迭代形态梯度算子解调信号频谱图3 迭代形态梯度算子分析

令任意选择的结构元素[0 1 0；1 1 1；0 1 0]发生变化，用于仿真信号的重复分析。计算表明，分析结果具有一致性，算法准确稳定。

3 轴承故障信号分析

试验对象为安装在齿轮箱上的轴承，轴承型号SKF6205-2RS，转速为1 772 r/min，承受径向载荷，采样频率为12 kHz，采样点数2 000。在测试轴承内圈电蚀加工单点故障，故障直径为0.18 mm。加速度传感器安装在电动机外壳上驱动端，由1台16通道的DAT记录仪收集振动信号。

根据轴承故障频率公式，当故障位于内圈时，故障频率为160 Hz。

图4为轴承故障的加速度振动信号。任意选择结构元素[0 1 0；1 1 1；0 1 0]进行分析比较。

图4 轴承故障信号

图 5为采用形态梯度算子对信号进行的分析结果，形态梯度算子能够提取出轴承故障信息(162 Hz)，但由于低频干扰(60 Hz和102 Hz)对判断带来严重影响，无法正确判断轴承故障。

图5 形态梯度算子分析频谱

而从图6中可以看出，迭代梯度算子所提取的信号冲击特征频率及其倍频十分明显(162 Hz和324 Hz)，可以有效地对轴承故障状态进行准确判断。可见，在随意选择的结构因子下，形态梯度算子受到低频信号的干扰，判断故障的能力有所减弱，而基于迭代的形态梯度算子却能有效地避免这种情况，准确提取出故障信号。

图6 迭代形态梯度算子分析频谱

对试验数据进行多次采样，并令任意选择的结构元素[0 1 0；1 1 1；0 1 0]发生变化，用于试验数据的分析。计算发现，分析结果具有一致性，结果准确稳定。

4 结束语

形态滤波是一种非线性滤波方法,可利用预先定义的结构元素对信号进行匹配,达到突出特征的目的。采用迭代形态梯度算子进行迭代，对信号处理，既抑制了噪声,又充分突出了故障信号的冲击特征。与形态梯度算子相比，结构元素的选择上具有随意性，能够在干扰环境下有效提取出脉冲信号，且不受低频干扰频率的影响；与传统的故障诊断方法比较，该方法计算简单、快速并易于实现。