基于Matlab的Hertz接触参数和主曲率差函数关系的拟合

刘胜超，王东峰，喻炜

(1.洛阳轴研科技股份有限公司 精密轴承制造部，河南 洛阳 471039；2.北京市三一重机有限公司，北京 102206)

符号说明

a—— 接触椭圆的长半轴

b—— 接触椭圆的短半轴

Dpw—— 球组节圆直径，mm

Dw—— 球径，mm

fi—— 内沟曲率系数

fe—— 外沟曲率系数

F(ρ)——主曲率差函数

Fa—— 轴向载荷，N

k—— 接触椭圆的椭圆率

K(e)——第一类椭圆积分

L(e)——第二类椭圆积分

Z—— 球数

ρ1Ⅰ——球在轴向平面的主曲率

ρ1Ⅱ——球在径向平面的主曲率

ρ2Ⅰ——套圈在轴向平面的主曲率

ρ2Ⅱ——套圈在径向平面的主曲率

α——初始接触角，(°)

φ——椭圆积分变量

γ——无量纲参数，γ=(Dw/Dpw)cosα

Hertz接触参数求解过程中，K(e)，L(e)和k是由循环迭代的方法求得的，迭代次数非常多，每次迭代都需要求解K(e)和L(e)，计算量大。这里利用Matlab曲线拟合工具箱，对K(e)，L(e)，k分别与F(ρ)进行拟合，得到它们和主曲率差函数F(ρ)的表达式，用拟合的结果求解给定型号轴承的其他Hertz接触参数，并与Hertz接触理论值以及最小二乘法线性回归法(回归法)得到的简化式[1]求得的结果进行对比。

1 Hertz接触参数

下面主要介绍与椭圆积分以及椭圆率计算相关的一些Hertz参数，其他参数不再赘述，可见文献[2-3]。

1.1 接触点的主曲率

在接触点，球与沟道表面的主曲率描述了球和沟道表面在接触点的几何特征，其影响到接触应力与变形及轴承动态性能[4]。球和沟道表面的主曲率计算方法见表1。

表1 球轴承接触点主曲率计算公式

主曲率差及主曲率和分别为

(1)

∑ρ=ρ1Ⅰ+ρ1Ⅱ+ρ2Ⅰ+ρ2Ⅱ。

(2)

1.2 椭圆积分

第一类完全椭圆积分为

(3)

第二类完全椭圆积分为

(4)

椭圆率为

k=b/a。

(5)

F(ρ)可以由K(e)，L(e)和k表示为[5]

(6)

2 拟合法及回归法

Matlab中提供的曲线拟合工具箱(Curve Fit Toolbox)可以对工作空间中的2组参数的数据点进行拟合，根据不同的拟合规则得到2个参数的表达式。这里利用Matlab曲线拟合工具箱，对K(e)，L(e)和k分别与主曲率差函数F(ρ)进行拟合，得到它们和主曲率差函数F(ρ)的表达式。

2.1 L(e)与F(ρ)的拟合

L(e)和F(ρ)的拟合曲线如图1所示。L(e)和F(ρ)的数据能用四次多项式很好地拟合出来，即

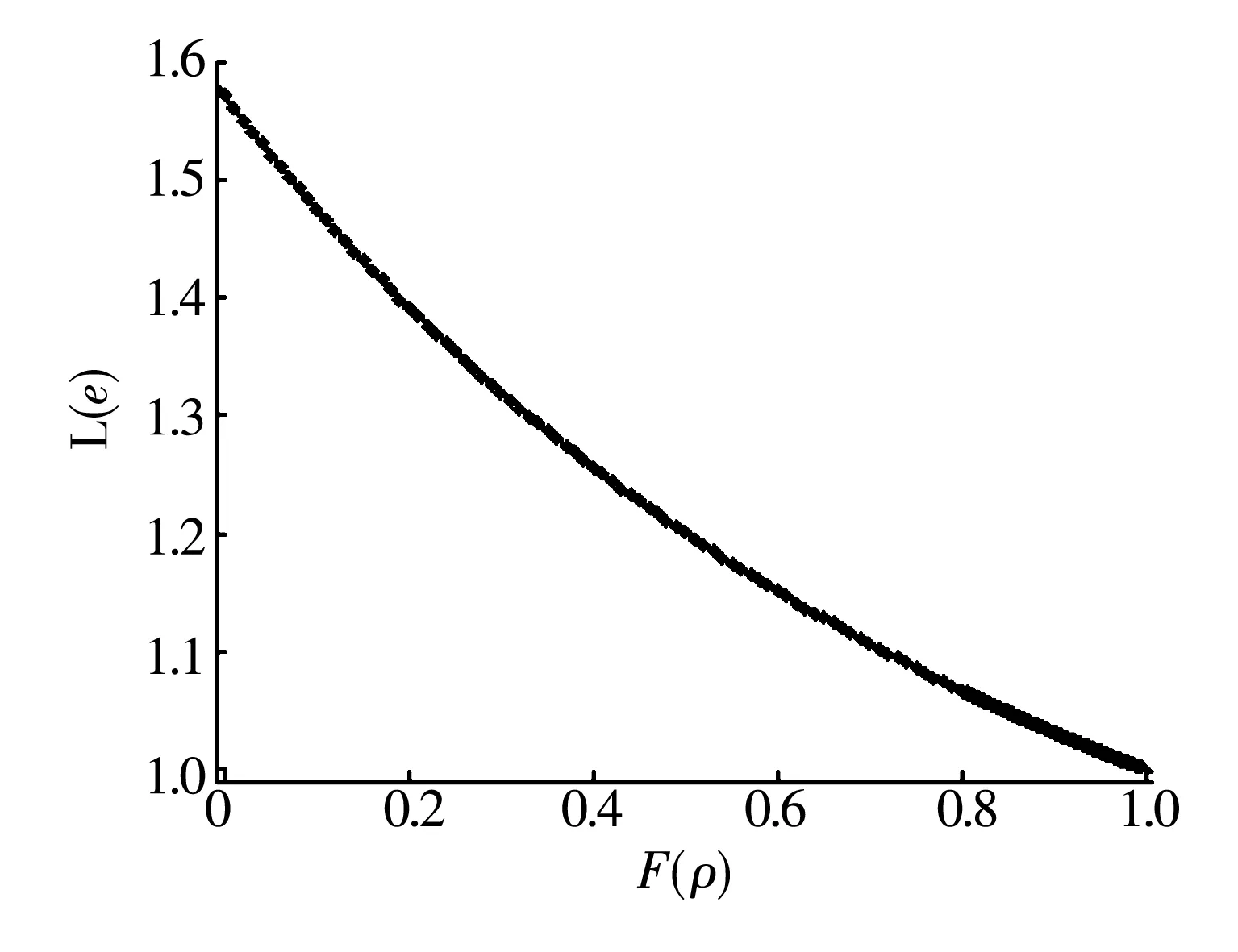
图1 L(e)和F(ρ)的拟合曲线

L(e)=0.131 8F4(ρ)-0.449 4F3(ρ)+0.783 4F2(ρ)-1.036F(ρ)+1.57，

(7)

L(e)随F(ρ)的增加而减小。

2.2 K(e)，k与F(ρ)的拟合

由于K(e)和k用多项式进行拟合时的误差较大，采用三次样条插值拟合法分别对它们与F(ρ)进行拟合，拟合的曲线如图2、图3所示。K(e)随F(ρ)的增大而增大，且在F(ρ)趋近于1时趋于∞；k随F(ρ)的增大而减小，二者几乎呈线性关系。

图2 K(e)和F(ρ)的拟合曲线

图3 k和F(ρ)的拟合曲线

由于K(e)，k与F(ρ)拟合的结果无法用简单的解析式表示出来， 因此将拟合结果保存至Matlab主工作区中KeFitted和kFitted两个mat文件，求解时，在主程序中调用这2个函数来计算K(e)和k。

2.3 回归法

由文献[1]知，由回归法求得的k，L(e)和K(e)的简化关系式为

(8)

(9)

(10)

3 实例分析结果

表2 球轴承参数

表3和表4分别给出了由拟合法和回归法得到的7208C/P4和B7019C/P4轴承的接触参数值，并比较了其与Hertz接触理论值的相对误差。结果显示，拟合法与Hertz接触理论值之间的误差更小，最大不超过0.6%；而回归法的最大误差将近1.8%。所以，拟合法不仅可行，而且更为准确。

表3 7208C/P4不同方法求得的接触参数值及相对误差

表4 B7019C/P4不同方法求得的接触参数值及相对误差

4 结束语

借助Matlab拟合出了椭圆积分、椭圆率与主曲率差函数的关系，用该拟合方法求解Hertz接触参数避免了大量的循环迭代过程，节省了计算时间，同时由该方法计算得到的参数值比回归法得到的参数值更为精确。