风电轴承多工况试验载荷谱的编制

陈观慈, 贾平, 毛范海, 孙守林

(大连理工大学 机械工程学院,大连 116024)

通过试验采集或模型仿真得到的机械零件工作载荷通常为时间历程载荷，由于采样时间较短，载荷的数据量大、变化频率快，将工作载荷直接用于零件疲劳寿命预测、设计和试验会带来无法克服的困难，如进行零件疲劳寿命试验时的液压加载一般无法达到数据采样频率的加载速度，因此，需要将零件的工作载荷重新编谱，既保留原始工作载荷特性，又方便零件的设计和试验。

文献[1]研究了全尺寸加速疲劳试验的时间历程载荷生成方法，将原始载荷统计分类为3种循环，将幅值较小的载荷循环忽略，载荷次循环与载荷主循环进行一定的合并，主循环出现的次序保持不变，从而重新生成时间历程载荷谱，获得了较好的效果。文献[2]采用神经网络方法仿真了随机载荷历程，其中考虑了雨流载荷循环的次序影响，模型中包含了载荷循环的概率密度函数。文献[3]研究了30年来标准化载荷谱和时间历程的产生和应用，研究认为载荷编谱准则的选用应视具体应用而定。文献[4]采用雨流计数方法对多轴载荷进行了统计分析，进而研究和提供了一种从原始载荷提取导致零件疲劳破坏的多轴载荷片段的方法。文献[5]从多参数载荷谱的角度对发动机气动载荷与机动载荷的匹配进行了研究，针对不同构件给出了不同的多参数载荷谱的处理办法。并以某发动机外场飞行参数数据为基础，对其进行了2种载荷的匹配分析。文献[6-7]针对航空领域的载荷谱编制和应用进行了富有成效的研究，具有高置信度中值随机疲劳载荷谱已应用于飞机设计中。文献[8]在机械领域抗疲劳设计方面也有显著的成绩。

许多学者在不同领域研究和实现了载荷谱的编制，但关于风电轴承载荷的编谱研究相对较少。风电载荷具有复杂的随机特性，而且风机使用过程中经常出现正常启停、发电、故障启停等工况条件，这些工况发生次序不定，导致风电轴承承受的载荷随机性强、工况类型较多，一年中交替发生数十种不同类型工况。上述风电轴承载荷特点给风电轴承的设计和应用带来诸多不便，特别是风电轴承的试验加载，基于此目的，开展多工况风电轴承载荷谱的编谱研究，为风电轴承的结构设计以及疲劳寿命试验奠定基础。

1 原始载荷的统计分析

原始载荷通过雨流计数统计得到载荷不同大小的幅值及均值的循环作用次数[4]，根据其作用次数可以计算幅值和均值的出现概率，将载荷幅值xa和均值xm视为二元随机变量，用二维概率分布来描述载荷幅值和均值的联合分布，即

(1)

式中：f(xa,xm)为变量(xa,xm)的联合概率密度函数。

为求得载荷幅值和均值的二维概率密度函数，首先对幅值和均值的2个边缘分布进行估计和检验，如风电载荷幅值近似符合Weibull分布，见 (2) 式；均值近似符合正态分布，见 (3) 式。然后考虑两者之间的相关性，根据其相关系数的大小确定一种合适的分布函数。

(2)

式中：f(xa)为幅值xa的概率密度函数；β为形状参数；ε为位置参数；α为尺度参数。

(3)

式中：f(xm)为幅值xm的概率密度函数;σ为形状参数；μ为位置参数。

2 试验载荷谱的编谱原理

2.1 多工况载荷幅值的复合概率密度

风电轴承承受数十种不同的载荷工况，编制轴承试验载荷谱时，需对所有出现的载荷工况予以统计，才能真实反映轴承的受载情况。求出所有单一工况载荷幅值的概率密度函数后，根据各单一工况在轴承工作时间内的作用次数比率获得其加权系数，通过加权系数合成多工况载荷均值的复合概率密度函数。各单一工况的权系数的计算式为

(4)

式中：ki为加权系数；Ni为载荷循环次数；N为载荷总循环次数；pi为工作时间占轴承总工作时间的比率；T为轴承总工作时间；ni为采样时间长度内载荷的总循环次数；ti为载荷采样时间；下标i为工况数,i=1,2,…,m。

第i个工况载荷幅值xa的概率密度函数为fi(xa)，则多工况载荷幅值的复合概率密度函数为

(5)

(6)

式中：εi,βi，αi分别为第i个工况下载荷幅值Weibull分布的位置参数、形状参数和尺度参数。

2.2 多工况载荷均值的总波动中心

二维载荷谱描述载荷幅值、均值与频次的关系，一维载荷谱仅表达载荷幅值与频次的关系。理论上将随机载荷的幅值和均值视为二元随机变量更接近实际，但应用难度加大。而一般认为，随机载荷的幅值变化对零件的疲劳寿命影响占优，载荷均值影响次之，因此目前常用“波动中心法”将疲劳载荷简化为一维随机变量进行统计处理。波动中心是所有载荷均值的总平均值，以波动中心作为载荷循环的静力成分，幅值作为动力成分，将幅值叠加到波动中心之上，从而编制载荷谱。单一工况载荷均值的波动中心为

(7)

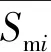
(8)

2.3 多工况载荷的编谱

已知多工况载荷幅值的复合概率密度函数，进一步对函数求积分可以获得多工况载荷幅值的概率分布函数。编制多工况风电载荷的试验载荷谱以此为基础，首先确定载荷幅值的最大值，以最大幅值为起点，将幅值划分为若干不同等级，通过概率分布函数确定不同等级幅值对应的发生次数，将载荷幅值与载荷均值的总波动中心叠加编制多工况风电载荷的试验载荷谱。按照目前国内外载荷谱制定时的共识，将发生概率为10-6的载荷幅值确定为最大幅值xamax，则

(9)

确定载荷幅值的最大值xamax后，可以设计试验载荷谱的幅值等级，即

xak=Kkxamax，

(10)

式中：xak为第k级载荷幅值；Kk为第k级幅值与最大幅值的比例系数。下标k为载荷分级，k=1,2,…,l。第1级至第k级载荷幅值的累积次数Nk为

(11)

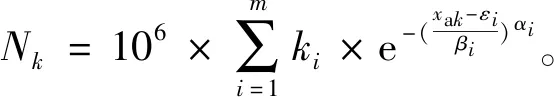
(12)

第k级载荷幅值的发生次数nk为

nk=Nk-Nk-1；k=2, 3,…,l。

(13)

3 应用示例

以某型1.5 MW风机主轴轴承为例，该轴承内径460 mm，外径655 mm，宽度184 mm。根据风场的气象条件，通过正常发电标准湍流风模型仿真，给出了35种工况条件的风机轮毂中心载荷和一年中的作用时间，35种工况载荷的相关仿真参数见表1，根据每种工况载荷一年中的作用时间比率扩展为20年内(风机设计寿命)每种工况的工作时间。每种工况载荷采样时间为10 min，通过力传递及平衡关系可以获得对应35种工况主轴轴承的当量动载荷。图1给出了第1种工况载荷的原始时间历程载荷，由图可知载荷具有较强的随机特性。

表1 35种工况载荷相关参数

图1 单一工况轴承的时间历程载荷

采用雨流计数法[4]对上述单一工况载荷进行统计分析，可以获得载荷幅值、均值和对应的循环作用次数，幅值和均值的三维直方图如图2所示，其中幅值和均值在各自的变化范围内划分为30等分。由图可以看出，在相同均值下，有若干不同等级的幅值，其总的作用次数与对应均值的作用次数相等。分别对载荷幅值和均值进行叠加，可分别得出30个等级载荷幅值和均值的循环次数，如图3和图4所示。观察载荷均值和幅值的分布，载荷幅值近似符合Weibull分布，载荷均值近似符合正态分布。

图2 单一工况轴承载荷的雨流统计

图3 单一工况轴承载荷的幅值统计

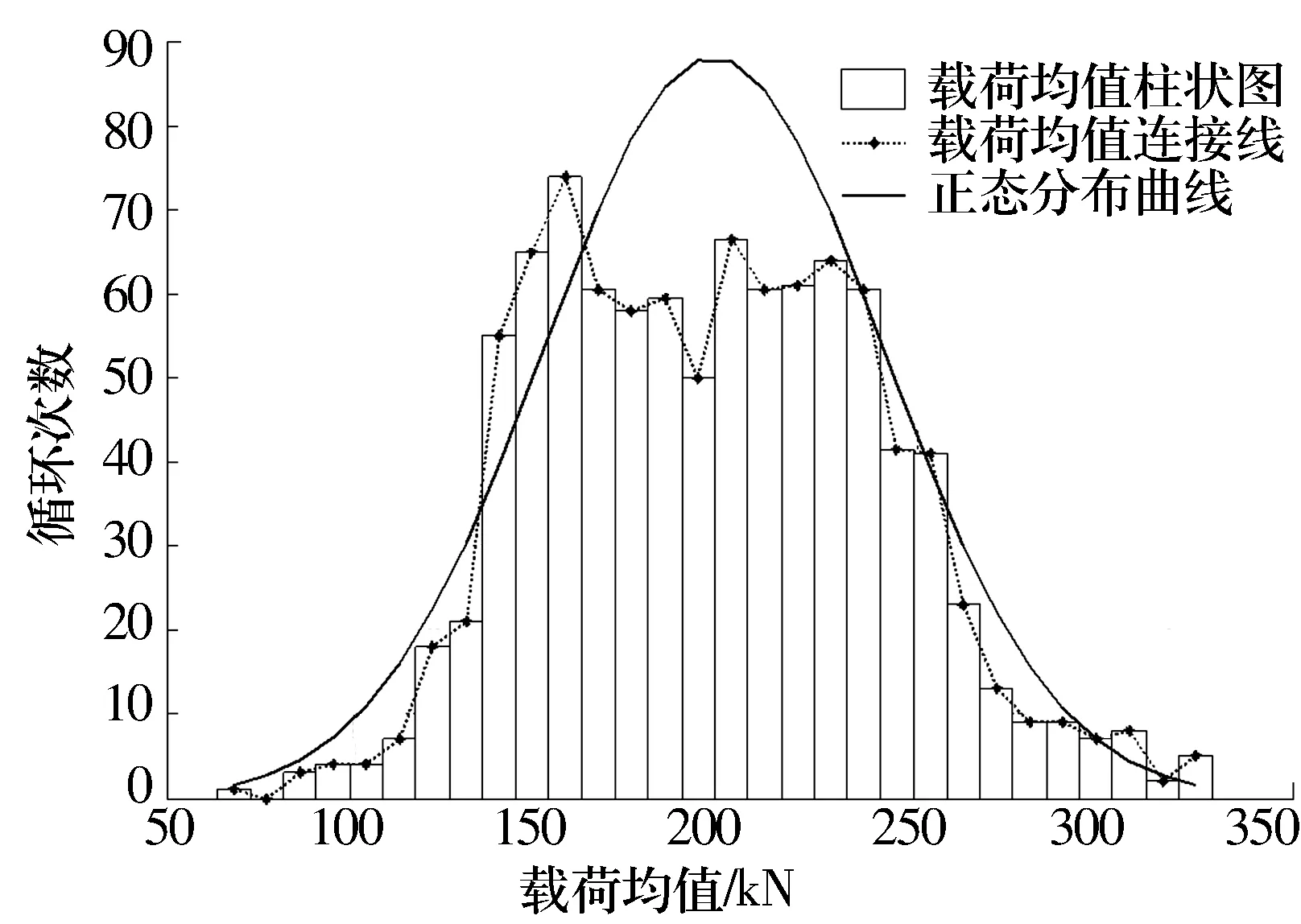
图4 单一工况轴承载荷的均值统计

表2 35种工况载荷幅值的Weibull分布参数

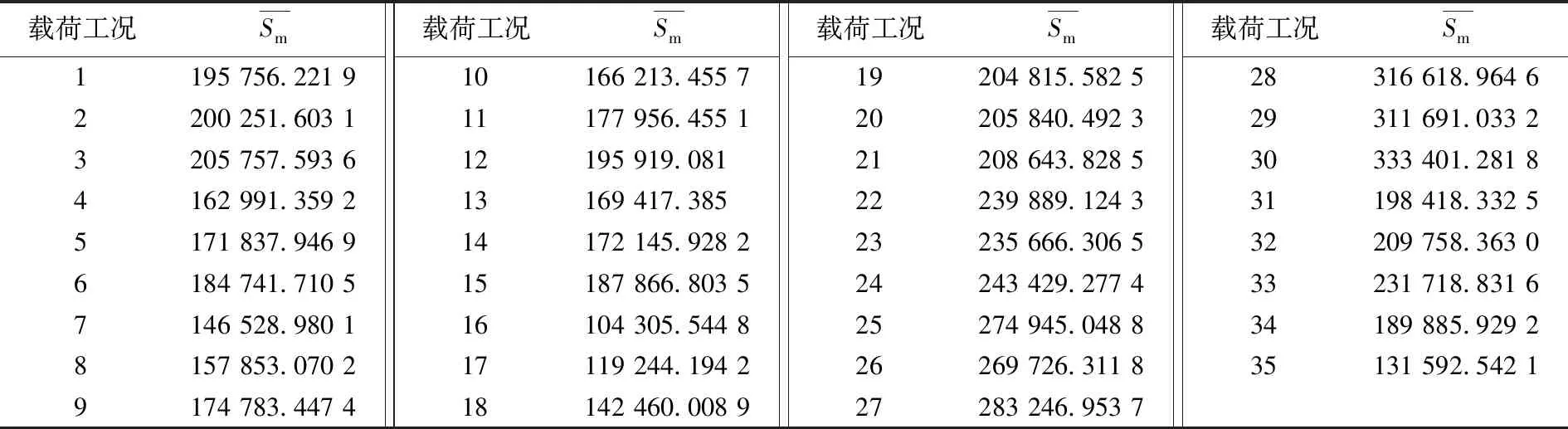
表3 35种工况载荷均值的波动中心

图5 多工况载荷幅值的Weibull分布

表4 35种工况载荷作用时间及加权系数

根据复合概率分布函数确定发生概率为10-6的幅值最大值，由于直接计算多工况载荷幅值的最大值较困难，因此采用Newton迭代法计算幅值最大值，将表2中的εi，βi，αi代入 (9) 式可得xamax=952277.7N，采用不等距法将载荷谱分为8级，比例系数Kk的选取见表5，由 (10) 式获得各级载荷幅值的值xak，由 (12)和(13) 式可以确定xa1至xak的累积作用次数Nk和xak的实际作用次数nk，详细数据见表5。

表5 多工况载荷的一维8级载荷谱

图6 多工况载荷对数累积次数及8级载荷谱

图7 载荷谱加载方式

4 结束语

针对风电轴承载荷随机性强、工况类型多的特点，研究了多工况风电轴承试验载荷谱的编谱

方法，该方法的核心是从原始载荷谱的雨流计数统计入手，寻求多工况载荷均值与幅值的复合概率分布特性，获取原始载荷的母体特性，将载荷幅值扩展分级为不同大小的具体数值，通过复合概率分布得到相应的作用次数。同时确定载荷均值的总波动中心，以载荷均值为静力成分，幅值作为动力成分，编制多工况风电轴承的试验载荷谱。最后以某型1.5 MW风机主轴轴承为例，在已知35种工况载荷及作用时间的前提下，采用前述编谱方法，编制了主轴轴承的8级试验载荷谱，该载荷谱具有35种工况载荷的母体特性，极大地方便了轴承的设计计算和试验加载。下一步将通过风电轴承疲劳寿命试验加以验证。