VM I合作企业利益协调策略研究

全春光，刘志学，程晓娟，王克喜

(1.华中科技大学 管理学院，湖北武汉430074;2.湖南科技大学 管理学院，湖南湘潭411201)

作为供应链成员间的合作方式之一，供给商管理库存(vendormanaged inventory，VMI)使供应链的库存管理、运输管理，以及订货管理更趋于合理，从而降低了供应链总成本。自20世纪80年代宝洁和沃尔玛成功实施VMI以来，其日益受到企业界和理论界的重视，国内外许多学者对此进行了研究，如 VMI对供应链性能的影响［1］以及VMI的补货决策［2-4］等。应指出的是，VMI加大了供应商的配送和库存管理等成本，并可能使供应商获得的利润减少。如果不对VMI系统的利益或成本重新分配，势必影响VMI的实施，于是一些学者开始关注VMI的利益协调或成本分担问题［5-9］。尽管需求确定情况下一对多的 VMI协调研究已取得了阶段性研究成果，但仍存在一些不足:文献［10］的成本模型中假定供应商与客户之间的补货采用批对批补货策略，这种假定虽然简化了建模过程，却给实际应用带来较大的局限;文献［11］建立利润模型时虽然假定供应商与客户之间的补货采用整数比补货策略，但其假定所有买方采用共同的补给周期，对需求确定且不允许缺货的一对多VMI而言，这种补货策略下的VMI系统获得的利润未必理想。

笔者在上述研究的基础上运用合作对策中的Shapley值法，探讨单供应商(假定为制造商)两分销商的VMI供应链库存成本节约的合理分配，在此基础上提出各成员的成本分担策略。其中，建立成本模型时假定供应商采用整数比策略，尤其在建立VMI三方合作成本模型时假定供应商对两分销商采用补货周期时间协调方式，以获得较低的系统总成本，这种补货策略可弥补现有VMI成本分担研究中成本建模方面的不足。

1 基本假设及符号说明

考虑由一个供应商，两个分销商构成的两级VMI供应链，单一产品情形，作如下假设:

(1)分销商需求与补货提前期确定，不允许缺货;

(2)供应商的生产率一定，且大于两个分销商的需求率之和;

(3)总成本只考虑库存持有成本及订货准备成本，不考虑运输成本;

(4)实施VMI前供应链为分销商主导型;

(5)成本建模时只考虑3种情况:供应商与分销商均不实施VMI、供应商只与一个分销商实施VMI、供应商与两个分销商均实施VMI;

(6)当任一分销商不合作时，两个分销商的补货时间即无法协同;

(7)为了降低库存成本，供应商尽可能采用整数比补货策略;

(8)在两个分销商均实施VMI的情况下，为了降低库存成本，供应商对两个分销商采用补货周期时间协调方式，即供应商补货周期分别为两分销商补货周期的整数倍。

模型符号说明如下:①节点i=0，1，2分别为供应商及分销商1和分销商2;②子系统i为供应商与分销商i组成的系统，i=1，2;③di为节点i的年需求量，i=0，1，2，且 d0=d1+d2;④p 为供应商的生产率(年生产量);⑤hi为节点i处单件产品的年库存持有成本，i=0，1，2;⑥Si为实施VMI前节点i每次的订单处理成本，i=1，2;⑦Sp为供应商每次的生产准备成本;⑧S0i为节点0(供应商)处理节点i每一个订单的固定成本;⑨Ti为节点 i的补货周期，i=0，1，2;⑩Tp为供应商每次生产时间;○11 Qi为节点 i的补货批量，i=0，1，2;○12 Q0i表示节点0为应对节点i的需求而需要的补货批量，i=1，2;○13 mi为节点 i补货批量的整数倍数，i=1，2;○14 TCi为节点 i的总成本，i=0，1，2;○15 TC0i表示节点0为应对节点i的需求而产生的成本，i=1，2;○16 TC 为 VMI供应链系统总成本;○17上标A，B，C，D分别为供应链的4种结盟形式。

2 供应商与分销商成本模型

2.1 供应商与分销商均不实施VM I(结盟A)

(1)分销商的补货策略及成本。在VMI实施前分销商将采用经济订货批量订货，分销商的订货批量为:

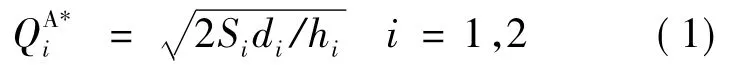
分销商的成本为:

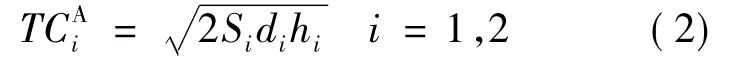
(2)供应商的补货策略及成本。根据假设(6)，该情况下一对二的供应链可以分解成两个独立的子系统。先计算子系统i(i=1，2)中供应商的补货策略及成本。

当分销商i以订货量QA*i订货，供应商的经济生产批量满足如下关系时，可使库存成本最小，即:

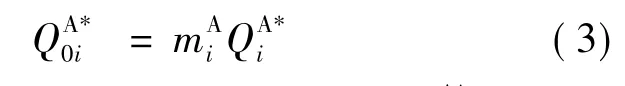
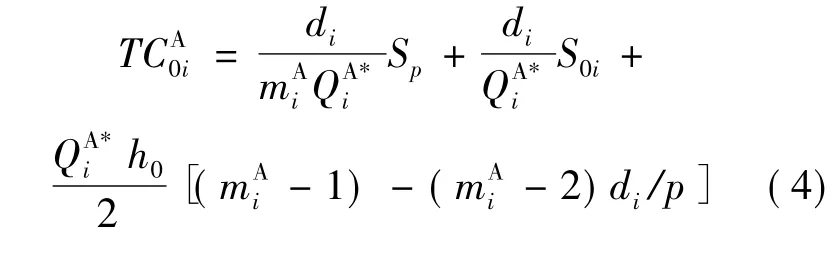
得到mA*i后，根据式(1)、式(3)和式(4)得到子系统i中供应商的最优补货策略及最小成本为:

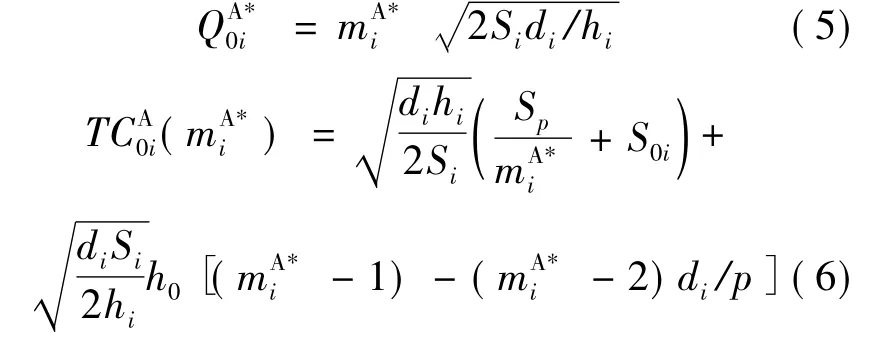
因此，供应商的总成本为两个子系统的成本之和，即:

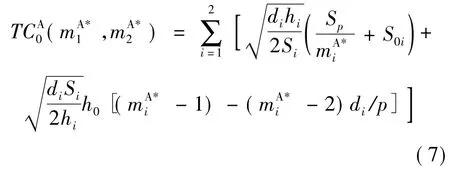
2.2 供应商只与一个分销商实施VM I(结盟B和C)

以供应商只与分销商1实施VMI(结盟形式B)为例建模，结盟形式C建模方法与此相同。

根据假设(6)，该情况下可将供应链分解成两个独立的子系统。子系统1实施VMI，子系统2则为分散独立决策情形。分别计算子系统i(i=1，2)中分销商、供应商的补货策略及成本。

2.2.1 子系统1

(1)分销商的成本。该模式下分销商不发生与库存有关的费用，因而TCB1=0;

(2)供应商的补货决策及成本。该模式下分销商的库存成本转移到供应商，供应商从子系统1总库存成本最小的角度做出补货决策。当对分销商的补货批量为QB1时，供应商自身的补货批量QB01应满足式(8)，才会使其总库存成本最小。

根据供应商的成本=处理分销商的订货成本及在分销商处的库存持有成本+生产准备成本+供应商的库存持有成本，可得供应商的成本为:

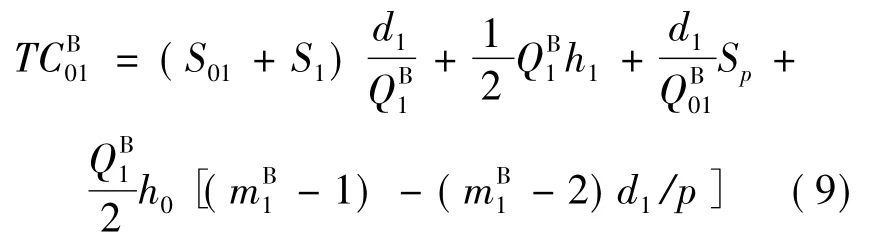
将式(8)代入式(9)并整理得:

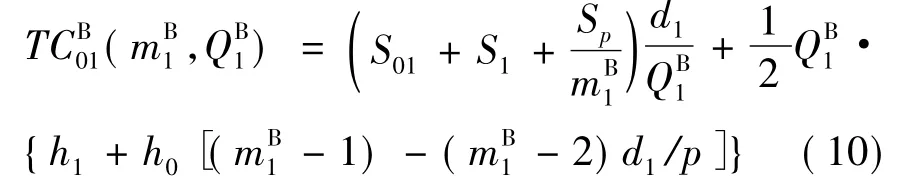
在此基础上求供应商的最优补货决策。将mB1，QB1看成连续变量，对式(10)求偏导，并令其等于零，求解得到:

如果式(11)计算出来的结果正好为整数，则它就是要求的结果;如果是小于1的数，则取1;如果不是整数，可以找出与mB1相邻的两个整数，它们是按mB1向下取整⎿mB1」和向上取整「mB1⏋。将式(12)代入式(10)，整理后有关mB1的供应商成本表达式为:

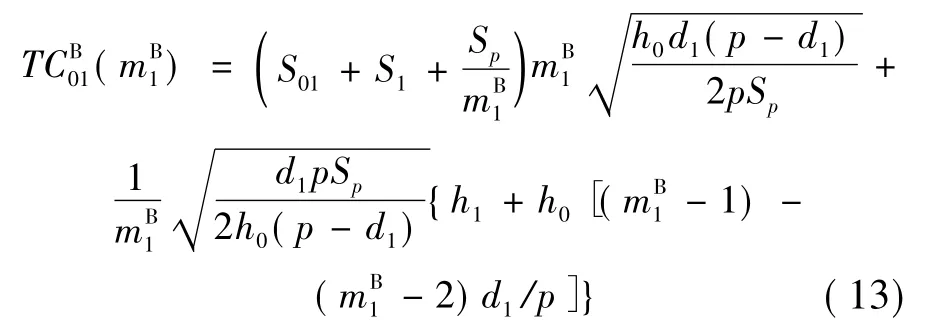
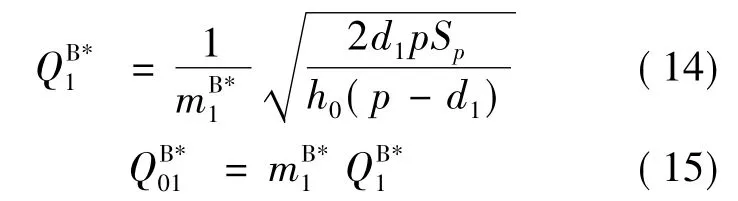
该决策下子系统1中供应商的最小成本为:

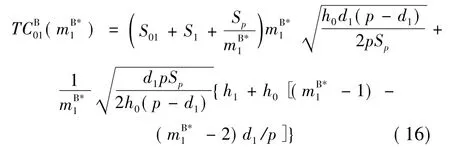
2.2.2 子系统2

参考式(1)、式(2)、式(5)及式(6)，有:

(1)分销商的补货策略及成本。分销商的订货批量为:

分销商的成本为:

(2)供应商的补货策略及成本为:

2.3 供应商与两分销商实施VM I(结盟D)

根据假设(8)，在节点0的一个补货周期TDO内，节点1正好有mD1次补货，节点2正好有次补货，因而有下列关系:

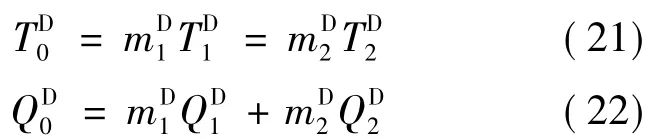
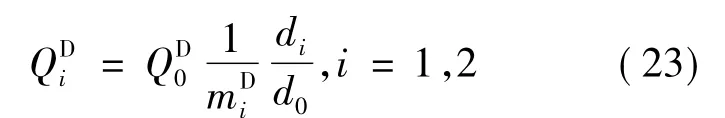
由文献［4］中的式(10)，长期运行下，VMI系统的总成本(生产购置成本为0)为:

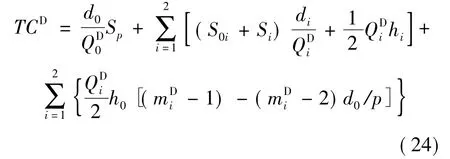
由式(23)，可将式(24)表达为:

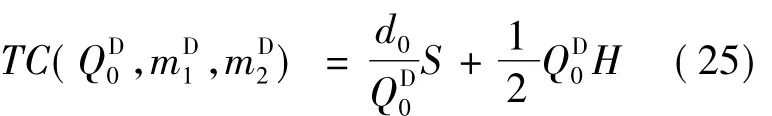
式中:

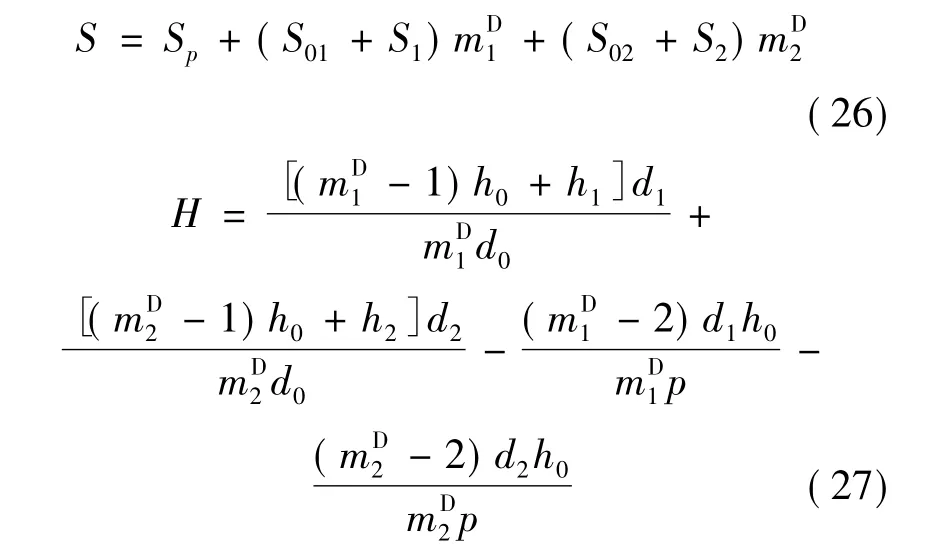
故总成本最小的VMI系统模型为:min TC(QD0，mD1，mD2)参考文献［4］关于m*1和m*2的求解，得到和后，各节点的最优补货批量为:

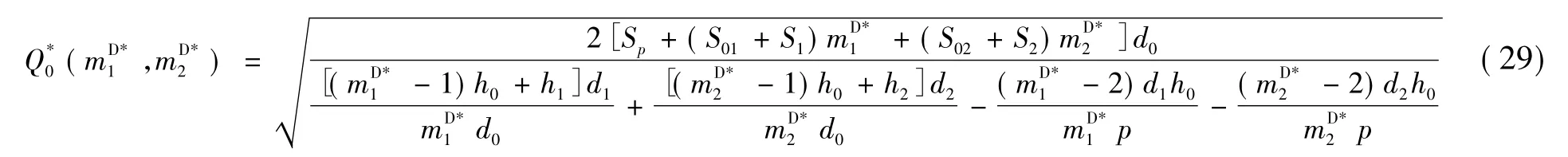
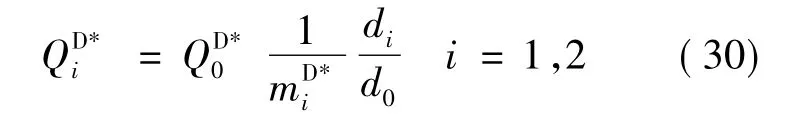
长期运行下，VMI系统的总成本为:

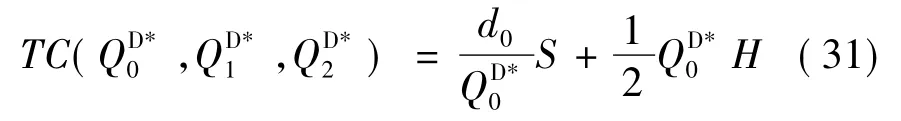
3 VM I成本分担的Shap ley值法

在Shapley值法中，Shapley值由特征函数v确定，记作

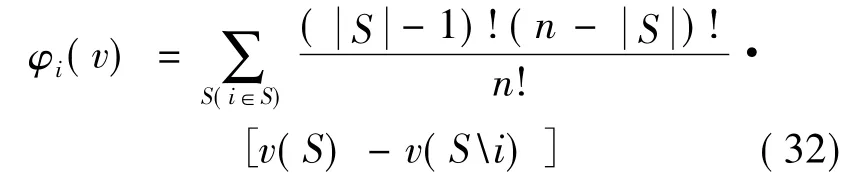
式中:S为N中若干企业联盟的子集;S为联盟中所含局中人的个数;v(S)为联盟子集产生的效益;v(Si)为子集S中除去企业i产生的效益。

单供应商两分销商的VMI供应链，可看成3人合作的联盟博弈问题，实施VMI后将发生库存成本的转移，联盟企业的成本分担问题可以转化为合作后的利益分配问题，从而可利用Shapley值法来解决。

将成本转化成效益，得到联盟S的效益ν(S)为:

4 算例分析

假定一供应商为两分销商供货，相关参数为:d1=560件/年，d2=4 500件/年，供应商生产率p=40 000件/年;库存持有成本分别为:h0=3元/(件·年)，h1=12元/(件·年)，h2=10元/(件·年);分销商订货处理成本分别为:S1=240元/次，S2=600元/次;供应商的生产准备成本Sp=5 500元/次，供应商处理分销商每一个订单的固定成本分别为S01=320元/次，S02=1 000元/次。

运用上述方法，借助Matlab软件及适当的算法，求得4种情况下系统的参数如表1所示。

由表1可知，如果两个分销商各自管理，则系统总成本为31 148元;如果供应商分别与分销商1、分销商2合作实施 VMI，则系统总费用降为30 766元、29 052元;若三者合作实施 VMI，则系统总成本为25 121元，达到最小。因此应选择三方合作实施VMI。

表1 数值计算结果

3个企业合作实施VMI时，可节约库存有关方面的成本，是一个多人合作对策问题，下面用Shapley值法来分配这个效益。

将数据代入式(33)有，v(0，1，2)=31 148-25 121=6 027。

3家企业合作实施VMI的效益为6 027元。用Shapley值作为这个效益的分配，得到供应商分配 φ0(v)=2 422，φ1(v)=1 374，φ2(v)=2 231。

最后，在供应商管理库存总成本25 121元中，各企业分担的成本:供应商为22 003-2 422=19 581元;分销商1为1 796-1 374=422元;分销商2为7 349-2 231=5 118元。

进一步将VMI实施前后各企业成本变化汇总，如表2所示。

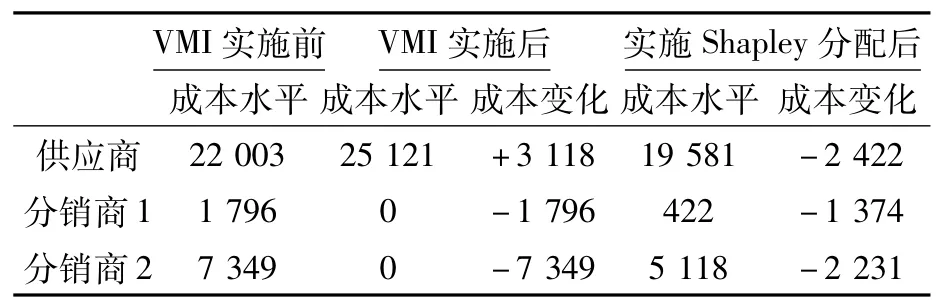
表2 VM I实施前后各企业成本情况变化汇总 元

由表2可看出，VMI实施后，虽然总成本降低了，但如不进行成本的重新分担，供应商成本将增加，两个分销商成本将减少。通过Shapley值法对成本重新分配后，三方的成本均有所下降。

5 结论

(1)建立了供应商与分销商不同合作形式下各方的库存成本模型。模型中考虑了供应商采用整数比补货策略;在两个分销商均实施VMI的情况下，模型考虑了供应商对两个分销商采用补货周期时间协调的方式。现有的关于VMI成本分担或利益协调的研究中均没有考虑该情形。

(2)在上述的库存成本模型基础上，运用Shapley值法对该VMI供应链中供应商与两个分销商因合作而产生的额外利益(库存成本的节约)进行了分配，然后在此基础上对VMI实施后库存成本的分担进行了重新分配设计。

(3)用算例验证了建模与成本分担方案。结果显示，VMI实施后，虽然总成本降低了，但如不进行成本的重新分担，供应商的成本将增加，而两个分销商的成本将减少。通过Shapley值法对成本重新分配后，三方的成本均有所下降，从而获得了一个联盟各方均满意的、稳定的分配方案。

［1］YAN D，XU K F.A supply chainmodel of vendormanaged inventory［J］.Transportation Research Part E，2002，38(2):75-95.

［2］WOO Y Y，HSU SL，WU SH.An integrated inventory model for a single vendor and multiple buyers with ordering cost reduction［J］.International Journal of Production Economics，2001，73(3):203-215.

［3］ZHANG T L，YU Y G，YU Y.An integrated vendormanaged inventory model for a two-echelon system with order cost reduction［J］.International Journal of Production Economics，2007，109(1/2):241-253.

［4］全春光，刘志学，程晓娟.整数比时间协调的VMI补货策略研究［J］.工业工程与管理，2010(4):35-40.

［5］WANG Y Z，JIANG L，SHEN Z J.Channel performance under consignment contract with revenue sharing［J］.Management Science，2004，50(1):34-47.

［6］GERCHAK Y，KHMELNITSKY E.A consignment system where suppliers cannot verify retailer’s sales reports［J］.International Journal of Production Economics，2003，83(1):37-43.

［7］曹武军.VMI环境下收入共享契约分析［J］.管理工程学报，2007，21(1):51-55.

［8］全春光.基于收益共享契约的VMI协调机制研究［J］.科学决策，2010(7):61-67.

［9］CACHON G P.Stock war:inventory competition in a two-echelon supply chain withmultiple retailers［J］.Operations Research，2001，49(5):658-674.

［10］刘建芬，胡奇英，李华.基于Shapley值法的VMI下合作企业间的费用分担策略［J］.系统工程，2005，23(9):80-84.

［11］YU Y，CHU F，CHEN H.A stackelberg game and its improvement in a VMI system with a manufacturing vendor［J］.European Journal of Operational Research，2009，192(3):929-948.