基于概率图模型的图像纹理模型*

杨 关，冯国灿，陈伟福，罗志宏

(中山大学数学与计算科学学院，广东省计算科学重点实验室,广东 广州 510275)

纹理分析已在图像分析中显示了它的重要性，比如遥感图像分析、医学图像分析、模式识别、计算机视觉和基于内容的图像修复。纹理是表现图像内容的基本视觉特征之一,可被看作是一种区域属性，包含的信息也不仅仅来源于单个像素,而是与像素邻域的灰度分布状况有关，不同尺度和分辨率的纹理，其特征是有差异的。纹理分析需要提取合适的特征用于纹理分类、分割和识别，特征提取就是将图像信息简化为一个小的特征描述集。因此，提取特征是纹理分析中重要的一步。大量的纹理特征和分类方法被提出，这些方法包括灰度共生矩阵[1]、小波、旋转不变算子、Gabor滤波器[2]、马尔科夫随机场(Markov Random Fields， MRF)模型和谱直方图等[2-4]。

概率图模型(Probabilistic Graphical Models)是关于图的多元统计模型[5-6]，是概率论和图论的结合，概率论描述各部分的依赖性，图论则直接指定各部分之间的关系，其主要前提就是用几个因子的乘积来表达一个随机变量集合的联合概率，每个因子仅仅依赖这个随机变量的一个小的子集。图模型是描述复杂高维系统的不确定性和复杂度的一个有力工具。对一个图模型，首先就是如何简洁地表现一个联合概率分布，然后再给定一些观察值推断出未知部分地状态，继而通过学习推断系统的结构和参数，最后根据推断出的结果做出决策。图模型根据基于有向图和无向图定义的概率分布集合，分为有向图模型(Directed Graphical Model)和无向图模型(Undirected Graphical Model)。图模型中的节点表示随机变量。无向图模型可以描述随机变量间的非因果联系。

高斯图模型(Gaussian Graphical Models，GGM)是一种特殊的图模型[5-7]，即模型中随机变量的联合概率分布服从高斯分布，这样就简化了图模型结构的学习过程,为描述纹理图像的空间特征和关联特征提供了一种简洁一致的建模方法。高斯图模型的模型选择是统计学研究的一个热点，但在图像纹理分析中应用较少。本文主要将高斯图模型应用于纹理分析并取得较好的实验结果。

要在一个规则图像网格上利用高斯图模型构建纹理模型，就需要找到某个点的灰度级与它的邻域点的灰度级之间的联系。这就带来两个问题，一是如何选择合适的邻域，另一个就是如何在大量的图像数据中估计参数。通过惩罚正则化进行模型选择是一个很好的方法。本文利用最小绝对选择和收缩算子(The least absolute selection and shrinkage operator，Lasso)[8]，弹性网格(Elastic Net)算法和自适应Lasso(Adaptive Lasso，aLasso)算法分别选择高斯图模型的邻域和估计参数[9-10]，建立新的纹理模型并用于纹理分析。本文中的高斯图模型是无向图模型。

1 高斯图模型

设零均值观察值X=(xs:s=(i,j)∈S)表示一个随机变量，且定义在一个有循环边界的M×N维图像网格S={(i,j):0≤i≤M-1,0≤j≤N-1}上。这里，要强调的是高斯随机变量的局部马尔科夫性和条件回归性之间的联系。

设无向图G=(S,E)，s∈S是图中的节点，设x-s={xr,r∈Ss}，考虑xs的条件分布p(xs|x-s)。利用标准的高斯性质[5]，条件分布p(xs|x-s)服从一个以x-s的线性权值和为均值且方差不依赖x-s的高斯分布。则可以分解xs为

(1)

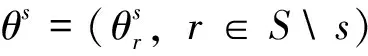
使用对于方程(1)，可将其改写为如下矩阵型

A(θ)X=e

(2)

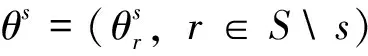
(3)

这里，X=(xs,s∈S)T是一个长度为MN的列向量，矩阵Xr是MN×(MN-1)维的矩阵，它的列由(xr,r∈Ss)T给出， 则高斯图模型的最小二乘估计就是

(4)

2 惩罚正则化方法

多元高斯图模型是根据马尔科夫性即条件独立性来定义，这种独立性反应在图上就是节点之间没有边相连。因而，变量选择也可通过检验独立性来完成， 即所对应的部分相关系数为零。从上节可看出，高斯图模型包含一个非因果的二维自回归过程，因此，惩罚性回归可被用于高斯图模型中选择邻域和估计参数。

由上节可知，最小二乘估计很不稳定。因此，惩罚性正则化技巧被提出用于改进最小二乘估计。L1惩罚项鼓励稀疏性(即将一些系数变为零)并同时给出变量选择后的参数估计。 最小收缩和选择算子(Least absolute shrinkage and selection operator,Lasso)就是将回归系数的残差平法和与L1惩罚项之和最小化[8]，因而Lasso算法可用于变量选择。Lasso估计就是能使下式最小化的参数

(5)

这里，λ是调谐参数(Tuning Parameter)。邻域选择(由λ所控制)通过L1惩罚回归的非零系数所定义。Lasso同时进行连续的减少和自动选择变量。

Zou等[9]提出一种新的正则化技巧，被叫做弹性网估计(Elastic net)，即对任意固定的非零参数λ1和λ2

λ2‖θ‖2

(6)

方程(6)是一个Lasso惩罚项和脊惩罚项(Ridge Penalty，即L2惩罚项)的凸性和[11]。同Lasso算法相类似，弹性网格估计也是同时自动选择变量和连续缩小。

被称作Adaptive Lasso(aLasso)估计[10]。“./”表示两个矩阵中位置相同的元素相除。值得强调的是方程(7)仍然是一个凸优化问题，因此，不会出现多个局部最小值，且全局最小值可被有效解出。如果有一个合理的初始估计可利用，则在合适的条件下，aLasso可正确的选择变量。aLasso算法有两个优点：①选择过程是连续的，因而是稳定的；②这个优化问题仍然是凸性的，因而更利于计算高维数据，比如图像。

3 算法的提出

3.1 基于高斯图模型的纹理特征提取

高斯图模型的模型选择对于建立纹理模型是非常重要的，模型的邻域应该包含那些最相关的像素点。不同的高斯图模型应该有不同的邻域结构。

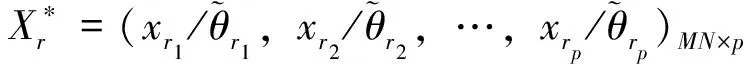
(8)

aLasso估计即可求出。以LARS算法为基础的LARS-EN算法则被用于求解弹性网格估计[9]。

每一个调谐参数λ将确定一个邻域和一组参数。λ越大，则非零系数的个数越少，若λ变小，则非零系数的个数越多，即邻域点的数目更多，当λ=0，这就是一般的LSE。利用上面所提到的LARS算法和LARS算法的变形分别求解Lasso、aLasso和弹性网格估计，得到所有λ对应的解。因此，要得到合适的邻域和参数就必须选择一个适当的调谐参数λ。本文使用贝叶斯信息准则(Bayesian Information Criterion，BIC)的一个变形选择合适的λ[13]

(9)

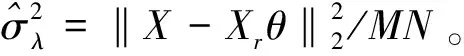
3.2 纹理合成算法

得到高斯图模型的邻域结构和参数估计后，基于高斯图模型的纹理特征参数的纹理合成算法将被讨论。为计算的方便，需要加一个平稳性的约束，平稳性是一种特殊的性质，它对于图G和高斯随机变量的逆协方差矩阵的元素是一个很强的假设[7]。对于方程(2)，图G定义在一个循环网格上，全条件概率p(xs|x-s)不依赖于点s位置的变化，这就使得A(θ)是一个块循环矩阵，块循环矩阵的特征结构也可被充分利用，因此，可利用块循环矩阵的特征值和特征向量与傅里叶变换的关系[7]来合成纹理，这样可充分利用块循环矩阵的特征结构。合成方程如下

(10)

这里，θ是块循环矩阵A(θ)的基，DFT2表示二维离散傅里叶变换。

从方程(10)中看到，要合成纹理就必须要确定高斯噪声e。e的相关矩阵是

E(eeT)=σ2A(θ)

(11)

VT[σ2A(θ)]V=Λ

(12)

这里，V是一个由σ2A(θ)的特征向量(正交的)组成的矩阵，Λ是对角矩阵，其对角线上的元素对应σ2A(θ)的特征值。因此，可以将e变换成为另一个随机变量，这个随机变量的元素是不相关的，即就是

ε1=VTe

(13)

其中，变量ε1的相关矩阵为VT[σ2A(θ)]V=Λ。此外，Λ1/2是一个对角矩阵，其元素是σ2A(θ)的特征值的平方根，则e可由下述方程所确定

e=VΛ1/2ε,

(14)

这里，ε～N(0,I)，I是一个M×N维的单位矩阵，将(14)式代入方程(10)中即可合成纹理。

3.3 纹理分类算法

(15)

这里xs是s点的灰度值，xr是点s的邻域点的灰度值。采用最大后验概率分类测试纹理图像，哪一类纹理的后验概率最大，即上式最小，则测试纹理图像就属于哪一类。

4 实验结果

为了检验所提算法的有效性，这里设计了两组实验，一个是纹理合成实验，另一个就是纹理分类实验。这两组实验都是基于高斯图模型和4阶高斯马尔科夫随机场模型[2-3]。

实验中的纹理样本均来自Brodatz 纹理库[14]。

4.1 纹理合成

这组实验使用四种Brodatz纹理，分别是D19、 D49、 D68和 D84。利用前面介绍的GGM的模型选择的方法提取纹理特征，并随机生成一个高斯随机白噪声ε～N(0,I)，然后通过方程(10)获得合成的纹理图像。这里采用高斯马尔科夫随机场纹理特征与基于GGM的纹理特征相比较[2-3]，图1显示了利用两种纹理特征合成纹理图像的结果。

图 1 纹理合成的实验结果

从图1中可以看出，使用基于高斯图模型的纹理特征合成的纹理(第三行到第五行)比基于高斯马尔科夫随机场纹理特征合成的纹理(第二行)更接近真实纹理。三种高斯图模型的模型选择方法很好的反应了纹理的方向特点，其中，基于aLasso的纹理特征最接近真实纹理。从统计角度来看，每个像素点的邻域是由与该点最相关的点构成而不一定是与该点距离最近的那些点。因此，图模型的邻域点更好地反应了像素点之间的相关性。

4.2 纹理分类

从Brodatz 纹理库中挑选25个不同的纹理图像组成一个纹理库，25个纹理图像如图2所示。

图 2 纹理图像

每幅图像的大小是640×640像素，且每幅图像可被看成是一类纹理。从每幅纹理图像中采集128×128像素的子图像81幅，则测试纹理集就由2 025(81×25=2 025)幅图像构成。所有2 025幅纹理图像样本都被放在训练集中，并计算出每一类训练样本的纹理特征。同样采集2 025幅128×128像素的子图像构成测试集，并计算出每一个测试样本的纹理特征。实验中我们分别使用高斯图模型纹理特征，小波纹理特征和4阶高斯马尔科夫随机场纹理特征进行纹理分类[2]，实验结果如表1所示，显然基于高斯图模型的纹理分类效果更好，同纹理合成实验的结果相类似，基于aLasso估计的纹理特征更接近真实纹理，因而分类准确率最高。

5 结 论

高斯图模型具有完备的数学理论，包容性很强，内涵很广，可以充分利用建模对象的先验知识，有非常广阔的应用前景，高斯图模型在统计学研究中发展很快，但在图像分析应用较少。本文对高斯图模型在图像纹理分析的应用进行了探讨，利用高斯图模型建立新的纹理模型并用于纹理合成和纹理分类。Lasso估计、弹性网格估计和aLasso估计被用于学习高斯图模型的结构，即选择邻域和估计参数。这三种变量选择方法都是凸优化问题，因而有很高的计算效率，且模型选择是一个动态的适应性过程，可根据模型的不同自动调整。纹理合成和纹理分类实验显示基于高斯图模型的纹理特征更加有效，因而，利用高斯图模型来构建纹理模型是有意义的，同时也有很大的发展前景。

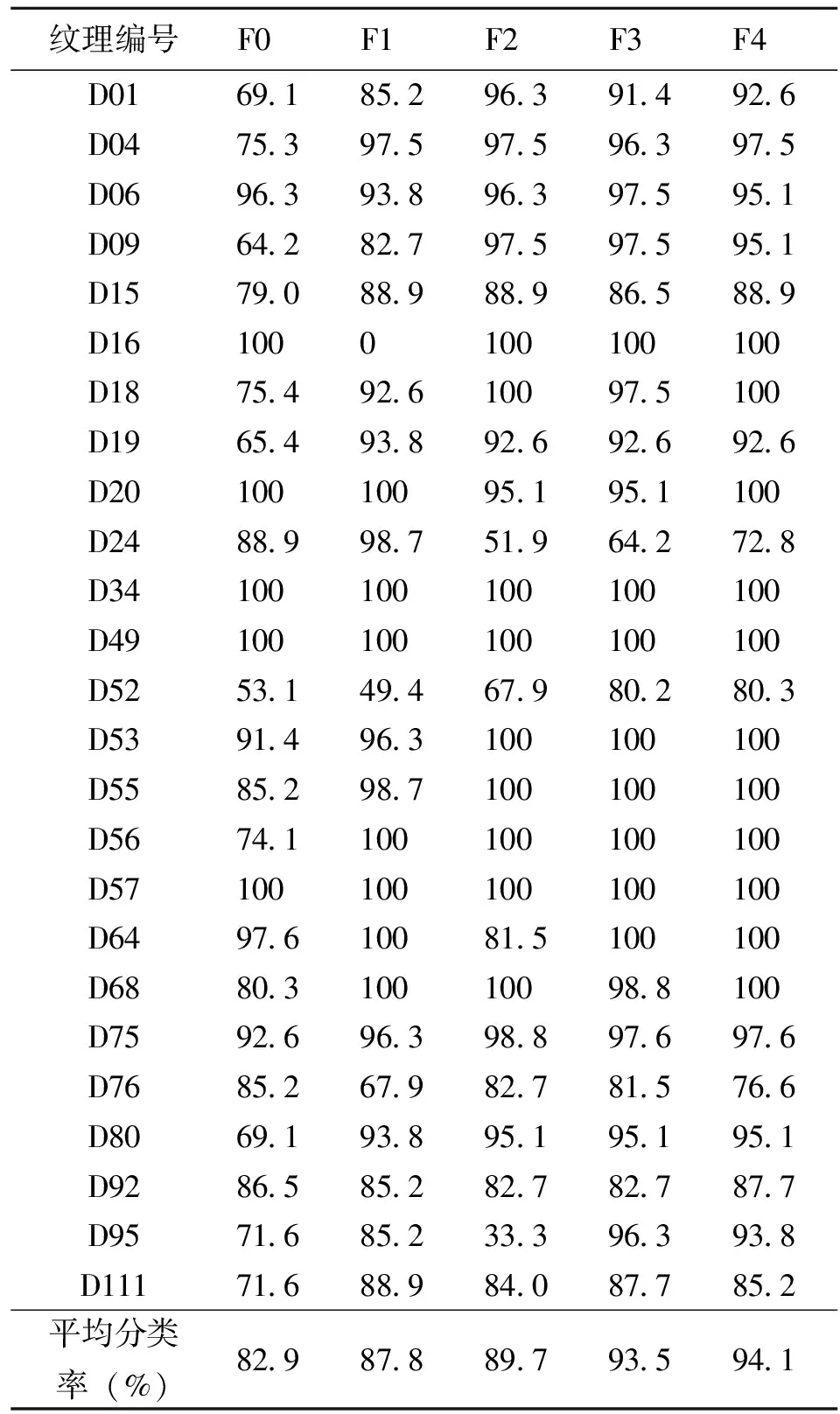
表1 不同方法的纹理分类结果比较(准确率%)1)

1)F0=基于小波的纹理特征；F1=基于4阶GMRF的最小二乘估计的纹理特征；F2=基于GGM的Lasso估计的纹理特征；F3=基于GGM的elastic net的纹理特征；F4=基于GGM的aLasso的纹理特征

参考文献：

[1]HARALICK R M, SHANMUGAN K, DINSTEIN I. Texture features for image classification [J]. IEEE Trans Syst, Man Cybern, 1973, 3(6): 610-621.

[2]PORTER R, CANAGARAJAH N. Robust rotation-invariant texture classification: wavelet, Gabor filter and GMRF based schemes [J]. IEE Proceedings in Vision, Image and Signal Processing, 1997, 144(3): 180-188.

[3]CHELLAPPA R, CHATTERJEE S. Classification of textures using Gaussian Markov random fields [J]. IEEE Trans Acoust, Speech, Signal Processing, 1985, 33(4): 959-963.

[4]LIU X, WANG D. Texture classification using spectral histograms [J]. IEEE Trans Image Processing, 2003, 12(6): 661-670.

[5]LAURITZEN S. Graphical models [M]. Oxford Statistical Science Series.Oxford:Oxford University Press, 1996.

[6]JORDAN M I. Graphical models[J]. Statistical Science,Special Issue on Bayesian Statistics, 2004, 19: 140-155.

[7]RUE H, HELD L. Gaussian Markov random fields: theory and applications [M]. Chapman & Hall/CRC, 2005.

[8]TIBSHIRANI R. Regression shrinkage and selection via the lasso [J]. J Roy Stat Soc, B, 1996, 58: 267-288.

[9]ZOU H, HASTIET. Regularization and variable selection via the elastic net [J]. J Roy Stat Soc, B, 2005, 67: 301-320.

[10]ZOU H. The adaptive Lasso and its oracle properties [J]. J American Stat Assoc, 2006, 101(476):1418-1429.

[11]HOERAL A, KENNARD R. Ridge regression [M]. In Encyclopedia of Statistical Sciences. New York: Wiley, 1988:129-136.

[12]EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression [J]. Ann Stat, 2004, 32(2): 407-451.

[13]WANG H, LI B L, LENG C. Shrinkage tuning parameter selection with a diverging number of parameters [J]. J Roy Stat Soc, B, 2009, 71(3): 671-683.

[14]WEBER A G. The USC-SIPI image database [M]. Version 5. USC-SIPI Report, Signal and Image Processing Institute, 2006.