关联大系统的静态输出反馈控制*

郭 岗，牛文生，崔西宁，朱 敏

(1. 洛阳师范学院信息技术学院，河南 洛阳 471022；2. 中国航空计算技术研究所，陕西 西安 710068；3. 西安通信学院，陕西 西安 710106)

基于T-S模型的模糊控制是研究非线性系统比较成功的方法之一，在非线性关联大系统的分散控制方面，已有不少成果面世[1-6]。但这些文献中T-S模型的模糊规则的后件部分都是一个线性模型。对于一些非线性系统，当用线性模型不能描述时，往往可以用双线性模型来描述。考虑T-S模型的有效性和双线性系统的特点，基于T-S双线性模型的模糊控制就引起了学者的关注。和常见的T-S模糊模型不同，模糊双线性控制系统模糊规则的后件部分是一个双线性模型。目前，在对双线性模糊控制的研究中，控制器大都是关于状态反馈的，关于静态输出反馈控制的结果则很少[7-10]。静态输出反馈控制直接利用系统的输出量来设计控制器，不用考虑系统状态是否可观测，而且静态输出反馈控制器结构简单，具有良好的应用价值。

本文研究了一类模糊双线性关联大系统的静态输出反馈控制问题。基于Lyapunov稳定性理论，得到了关联大系统渐近稳定的充分条件，并把这种条件转换成线性矩阵不等式(LMI)形式，相应的分散模糊控制器可以通过求解LMI得到。这种方法简化了设计程序，并由数例仿真验证了结果的有效性。

1 系统描述

一类由s个子系统组成的模糊双线性关联大系统，通过单点模糊化，乘积推理和中心平均反模糊化方法，可得系统的总体模型为

i=1,2,…,s,m=1,2,…,ri

(1)

根据并行分布补偿算法，考虑局部反馈控制器

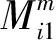
then

ρisinθim=ρicosθimFimyi(t)

(2)

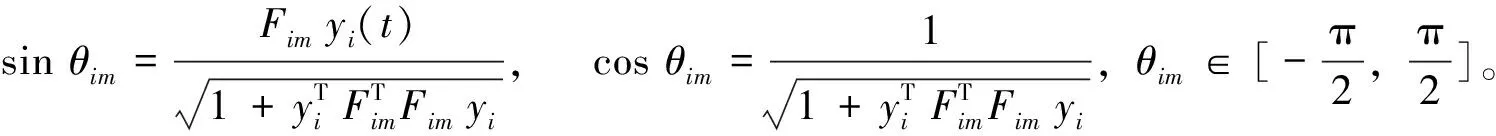
(3)

在控制律(3)的作用下，整个闭环系统的方程可表示为

(4)

这里Λi,mnl=Aim+ρisinθinNim+ρicosθinBimKinCil。

本文目标：对于由s个子系统组成的模糊关联大系统，对每一个子系统设计局部静态输出反馈控制器，使得闭环关联大系统(4)渐近稳定。

2 主要结论

定理1 对于给定的常数ρi>0,εi>0,如果存在矩阵Zi>0,和矩阵Fin,n=1,2,…,ri满足矩阵不等式(5)，则关联大系统(4)是渐近稳定的。

Φi,mnl=

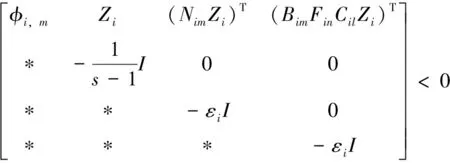
(5)

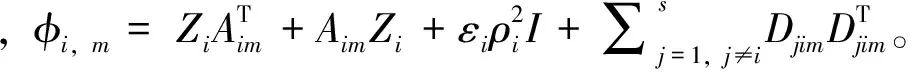
证明考虑选取如下Lyapunov函数

(6)

沿着系统(4)的轨线，对V(t)求导，可得到

(7)

考虑下式，并由文[11]中引理可知

(8)

同样考虑下式，并由文[11]中引理可得到

(9)

把(8)式、(9)式代入(7)式，可得到

(10)

这里

对定理1中的(5)式同时左、右乘diag{Pi,I,I,I}，则可得到

(11)

考虑(5)式是双线性矩阵不等式(BMI)，不能直接用Matlab中的LMI工具箱求解。为求解控制器，下面提出一个新的方法把BMI转换成LMI形式。

(12)

证明考虑

φi,mnl=

假设有Φi,mnl+φi,mnl<0，则可以得出Φi,mnl<0。考虑

Φi,mnl+φi,mnl=

由Schur补定理可知，(12)式等价于Φi,mnl+φi,mnl<0，进一步可以得Φi,mnl<0。根据定理1，则可知在静态输出反馈器下，闭环系统(4)是渐近稳定的。

3 算例分析

考虑2个子系统复合而成的不确定模糊双线性关联大系统。

Subsystem 1:

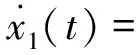
B11u1(t)+D211x2(t),

y1(t)=C11x1(t);

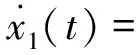
B12u1(t)+D212x2(t),

y1(t)=C12x1(t);

Subsystem 2:

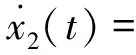
B21u2(t)+D121x1(t),

y2(t)=C21x2(t);

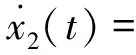
B22u2(t) +D122x1(t),

y2(t)=C22x2(t)，其中

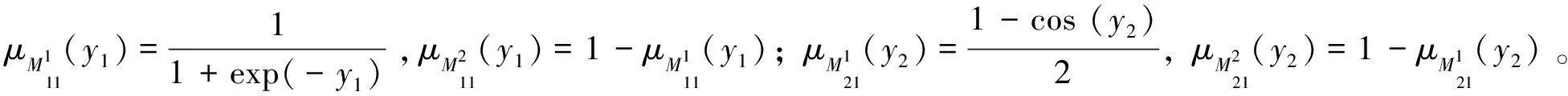
K11=[-1.067 1];K12=[-0.562 8];

K21=[-1.208 3];K22=[-1.623 9]

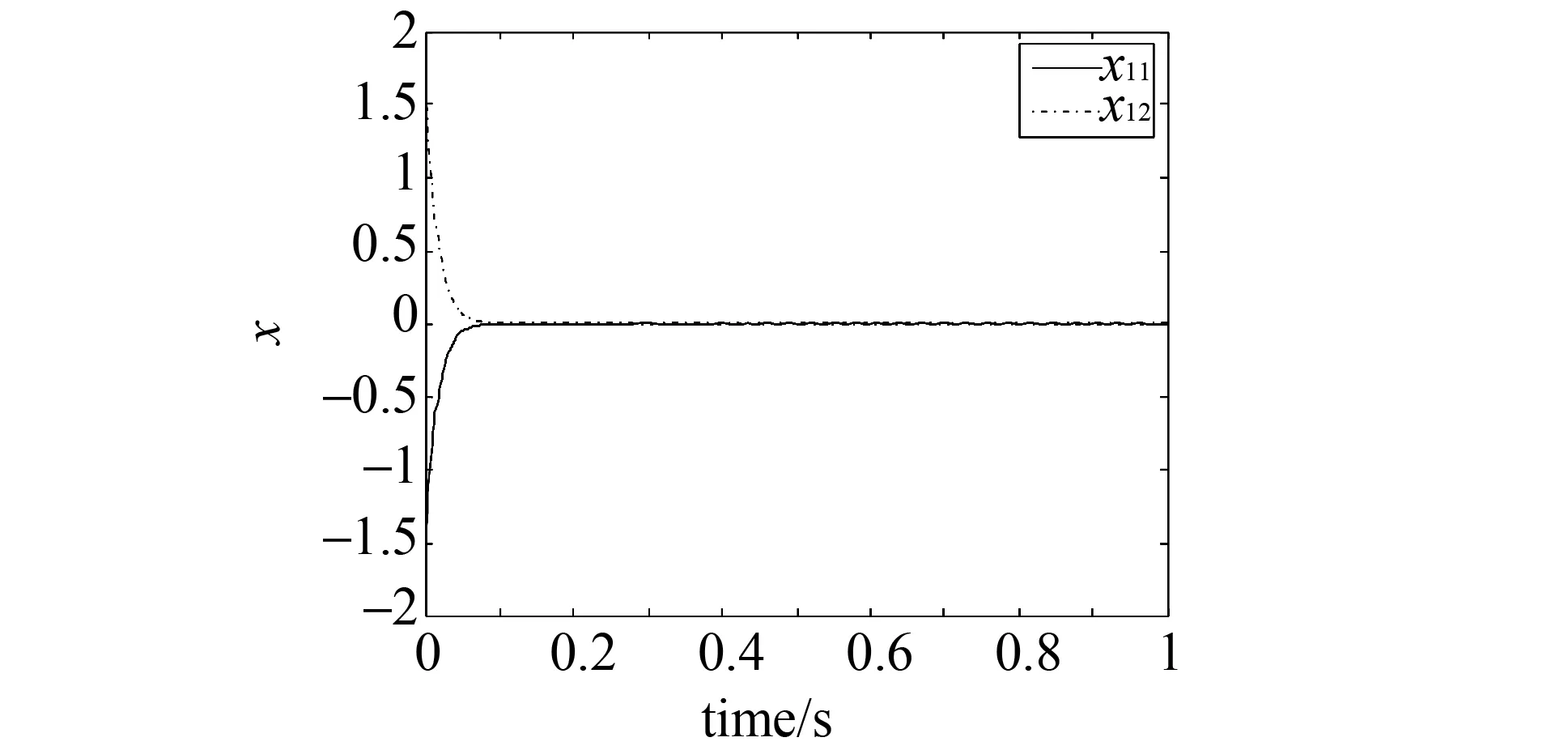
图1 子系统1的状态响应曲线

图2 子系统2的状态响应曲线

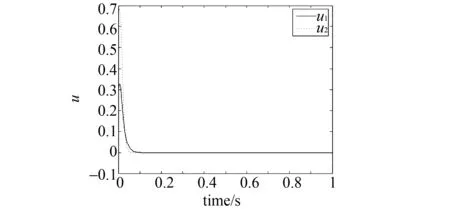
图3 控制曲线

参考文献：

[1] WANG W J, LUOCH L. Stability and stabilization of fuzzy large-scale systems[J]. IEEE Trans Fuzzy Syst, 2004, 12(3): 309-315.

[2] CHEN C W, CHIANG W L, HISAO F F. Stability analysis of T-S fuzzy models for nonlinear multiple time-delay interconnected systems[J]. Mathematics and Computers in Simulation, 2004, 66(6): 523-537.

[3] 张果，李俊民. 不确定时滞模糊系统的时滞相关鲁棒H∞控制[J]. 中山大学学报:自然科学版, 2009, 48(1): 10-15.

[4] 赵立英，刘坤，刘贺平. 具有两个时滞和的连续系统的时滞相关稳定性[J]. 中山大学学报:自然科学版, 2008, 47(1): 26-28.

[5] 郭岗，王子须，牛文生，等.基于T-S双线性模型的非线性关联大系统的分散控制[J].武汉大学学报：工学版，2010，43(4)：541-544.

[6] 郭岗，赵斌，牛文生，等.时变时滞模糊系统的稳定性分析[J].华中科技大学学报：自然科学版，2010，38(7)：130-132.

[7] LI T H S, TSAI S H. T-S fuzzy bilinear model and fuzzy controller design for a class of nonlinear systems[J]. IEEE Trans Fuzzy Syst, 2007, 15(3): 494-505.

[8] TSAI S H, LI T H S. Robust fuzzy control of a class of fuzzy bilinear systems with time-delay[J]. Chaos Solitons and Fractals, 2009, 39(5): 2028-2040.

[9] LI T H S, TSAI S H, LEE J Z, et al. Robust H∞fuzzy control for a class of uncertain discrete fuzzy bilinear systems[J]. IEEE Trans Syst, Man Cybe, 2008, 38(2) : 510-526.

[10] KAU S W, LEE H J, YANG C M, et al. Robust H∞fuzzy static output feedback control of T-S fuzzy systems with parametric uncertainties[J]. Fuzzy Sets and Syst, 2007, 158:135-146.

[11] WANG R J, LIN W W, WANG W J. Stabilizability of linear quadratic state feedback for uncertain fuzzy time-delay systems[J]. IEEE Trans Syst Man Cybe, 2004, 34(2): 1288-1292.