滚动轴承故障的全矢小波分析
2011-07-23韩捷王宏超陈宏巩晓赟王植申
韩捷,王宏超,陈宏,巩晓赟,王植申
(郑州大学 振动工程研究所,郑州 450001)
滚动轴承是旋转机械中应用最为广泛的机械零件,也是最容易损坏的元件之一。滚动轴承的检测诊断技术有很多,如振动信号分析、声发射诊断、油液分析诊断和光纤监测诊断等,其中振动信号分析诊断技术应用最为广泛[1]。
滚动轴承出现故障时的振动信号是非平稳的,经典的分析方法如Fourier变换难以达到满意的效果。小波分析可同时从时域和频域两个方面对信号进行分析[2-3],再结合包络分析方法十分适于滚动轴承的故障特征提取,然而,这种方法是基于单通道信号进行特征提取的,仍存在信息量不足、同源信息特征不一致、特征不明显等弊端。而基于双通道信息的全矢小波分析方法不仅对单通道小波分析方法具有兼容性,而且还弥补了传统旋转机械用单通道信息进行特征提取造成的信息量不完整、易导致误诊的弊端。
1 全矢谱理论基础与计算方法
来自转子同一截面x,y两个方向的振动信息属于同源信息,平面全矢谱技术就是在转子同一截面上同时布置两个相互垂直的传感器对信号进行采集和揉合分析的方法。全矢谱分析的基本指导思想是:转子的涡动现象是各谐波频率下的组合作用,其涡动轨迹是一个椭圆,椭圆是两个同频率(Ω)、运动方向(角速度为ω)相反的圆轨迹的合成[4],两圆半径分别为Xpk,Xrk,即:Z=XpkejΩt+Xrke-jΩ t。
(1)
定义旋转机械单谐波下的椭圆轨迹长半轴为该谐波下的主振矢,用RLk(图1)表示;椭圆轨迹短半轴为该谐波下的副振矢,用RSk表示。
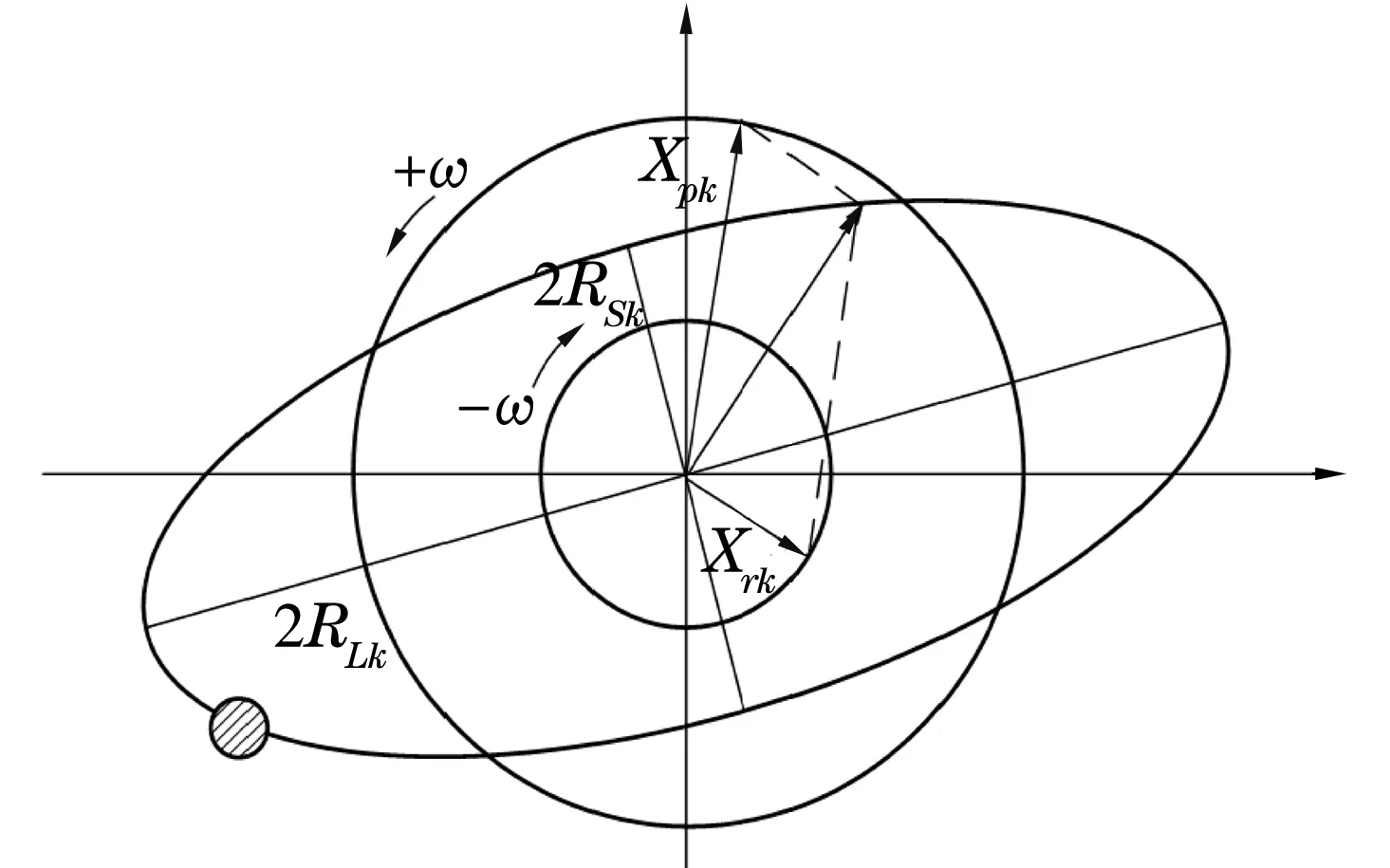
图1 两圆合成椭圆轴心轨迹图
假定{xn}和{yn}分别为x,y方向上的离散序列,其Fourier变换分别为{Xk},{Yk}(k=0,1,2,…,N-1),其中N为信号长度 ,XRk,XIk,YRk,YIk分别为Xk,Yk的实部序列和虚部序列。
用序列{xn},{yn}构成复序列{zn},即{zn}={xn}+j{yn}。
(2)
对其做Fourier变换,得到其离散Fourier变换{Zk},利用Fourier变换奇偶共轭的性质可以得到
(3)
式中:k=0,1,…,N/2-1。
由(1)~(3)式及Fourier变换的性质可得
(4)
式中:k=0,1,…,N/2-1。
这样,就实现了通过两个通道的数据序列做一次Fourier变换,从而得到全矢谱需要的各谐波轨迹的特征信息,不仅大大减小了计算量,同时也非常稳定。另外也和常规分析建立了联系,在信息源为单源时,该算法仍然成立,完全满足实时检测分析要求。
2 全矢小波分析方法[5]
根据多分辨率分析和正交小波变换理论可知[2-3],用正交小波函数
(5)
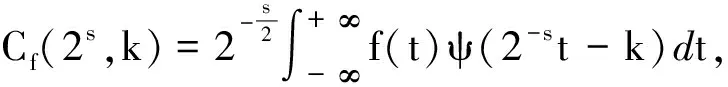
(6)
则水平方向和垂直方向的时域信号x,y作小波变换后的系数分别为
(7)
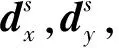
(8)

(9)
3 试验研究
采用某电气工程实验室的试验数据[6-7],试验装置由电动机、扭矩传感器/译码器、测力计和电器控制装置组成。两个加速度传感器(x,y)呈90°方向安装在接近电动机驱动端的轴承座上,转子转速为1 772 r/min,以采样频率fs=12 000 Hz来获得驱动端轴承外圈的512点个故障数据(数据单位为电压V),已知轴承外圈故障通过频率为105.8 Hz。试验轴承型号为6205-2RS。
x,y通道的时域和频域分析分别如图2、图3所示,x,y通道的4层小波分析如图4所示。

图2 x,y两通道时域图

图3 x,y两通道频域图

图4 x,y两通道小波分解示意图
分别对d1x,d1y(3 000~6 000 Hz)进行包络分析如图5所示。

图5 x,y两通道包络分解示意图
由图5可见,x通道细节部分的系数d1x重构后能较好的包络解调出轴承外圈故障通过频率105.8 Hz,而y通道细节部分的系数d1y重构后的包络效果并不理想。下面对其进行全矢小波分析,结果如图6所示。

图6 x,y两通道合成全矢小波分解示意图
从图6的全矢小波图中,可以明显的提取出32倍外圈故障通过频率3376 Hz,而图3所示的频谱图中,y通道3 376 Hz处的幅值特征并不明显。通过以上分析可知,全矢小波分析方法具有信息量完整、故障特征更明显等优点,相对于小波-包络分析方法有一定的优势。
4 结束语
试验证明,小波-包络分析方法虽然适用于滚动轴承的故障特征提取,然而这种方法基于单通道信号进行特征提取,仍存在信息量不足、同源信息特征不一致、特征不明显等弊端。而基于双通道信息的全矢小波分析方法不仅对单通道小波分析方法具有兼容性,而且弥补了传统旋转机械用单通道信息进行特征提取造成的信息量不完整、易导致误诊的弊端。
