多尺度柔性形态滤波在轴承故障诊断中的应用
2011-07-23杨杰郑海起刘晓平王彦刚
杨杰,郑海起,刘晓平,王彦刚
(石家庄军械工程学院,石家庄 050003)
滚动轴承存在局部缺陷时,其振动信号中的
脉冲信号含有丰富的缺陷信息。若能够有效地将缺陷引起的脉冲信号提取出来,便可诊断出缺陷存在的部位[1]。
形态学滤波器作为一种非线性滤波器,可以有效地提取信号的边缘轮廓以及形状特征,克服了线性滤波的不足。目前,形态滤波在旋转机械振动信号滤波方面已经有一定的应用[2],但是经典的形态学滤波在取单一结构元素的情况下存在缺陷[3],因此各种针对结构元素的改进算法相继出现,如基于权重的形态学运算[4]、多尺度结构元[5]和结构元的自适应优化算法[6]等。
文献[7]提出了柔性形态学(Soft Mathematical Morphology)的概念,研究表明柔性形态学对加性噪声和信号的微小变化不敏感,能同时去除信号中的正负噪声,并保留细节。文献[8]比较了柔性形态滤波(Soft Morphological Filter,SMF)和小波包的滤波效果,表明SMF在诊断外圈故障和滚动体故障时的优越性。
在此提出了一种多尺度柔性形态滤波(Multi-scale Soft Morphological Filter,MSMF)方法,并将其应用于轴承故障诊断。
1 数学形态滤波
1.1 基本形态运算
数学形态学的基本运算包括腐蚀、膨胀、开运算和闭运算。设一维信号f(n)为定义在F=(0,1,…,N-1)上的离散函数,结构元素g(n)为定义在G=(0,1,…,M-1)上的离散函数,且N≥M,则g(n)对f(n)的腐蚀和膨胀运算分别定义为
(fΘg)(n)=min[f(n+m)-g(m)],
(1)
(f⊕g)(n)=max[f(n-m)+g(m)],
(2)
式中:m∈(0,1,…,M-1)。
g(n)对f(n)的开运算和闭运算分别定义为
(f∘g)(n)=(fΘg⊕g)(n),
(3)
(f·g)(n)=(f⊕gΘg)(n)。
(4)
通常开、闭运算用于构成各种形态滤波器,而它们本身就是最基本的形态滤波器,且以不同的方式平滑信号。开运算可抑制信号中的正噪声;相反,闭运算可抑制信号中的负噪声。
1.2 柔性形态滤波
在柔性数学形态学中,结构元素被分割成硬核和柔性边缘两部分,经典形态算子中的最大最小运算在柔性形态算子中被排序统计所代替,且最主要的思想是引入了定义一种重复集。
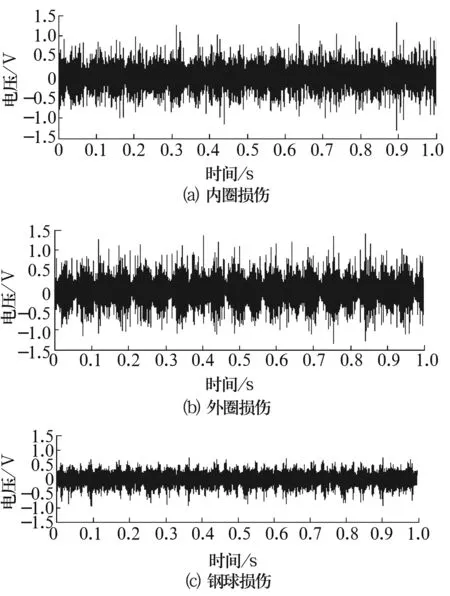
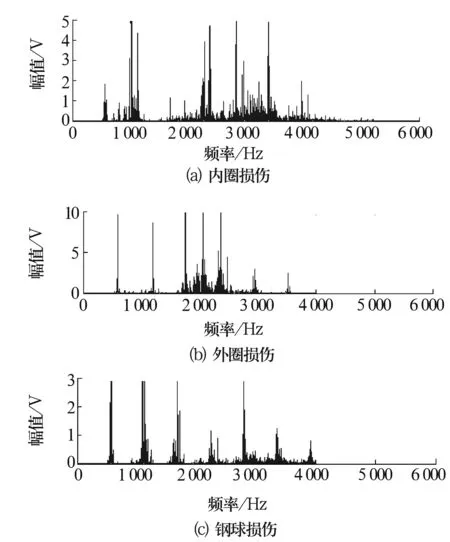
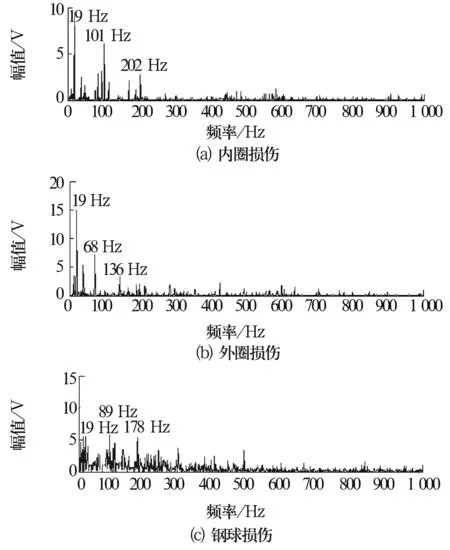
柔性形态学的结构系统由[B,A,k]3个参数组成,有限集A和B为定义在Z上的凸集,k满足于1 {k<>f(a)}={f(a),f(a),…,f(a)}, 式中:k为正整数,且1≤k≤min{|B|/2,|BA|},a∈B。 [B,A,k]对f的腐蚀和膨胀分别定义为 fΘ[B,A,k](x)=min(k){k<>f(a):a∈Ax}∪ {f(b):b∈(BA)x}, (5) f⊕[B,A,k](x)=max(k){k<>f(a):a∈Ax}∪ {f(b):b∈(BA)x}, (6) 其中,min(k)表示取第k小的值,同理max(k)表示取第k大的值。当k=1时,柔性形态变换与经典形态变换相同;当|A|=0时,柔性形态变换与顺序形态变换相同。 设A,B的映像集分别为AS,BS,则结构元素[B,A,k]对f进行形态开和形态闭运算定义如下 f∘[B,A,k]=(fΘ[B,A,k])⊕[BS,AS,k], (7) f·[B,A,k]=(f⊕[B,A,k])Θ[BS,AS,k]。 (8) 由以上定义可知,在柔性形态学运算中,落入到硬核区域中的信号数据权重较大,而落入到软核区域中的信号数据权重较小。因此,和标准形态学运算比较,柔性形态学运算具有更好的保持细节和抗噪声功能[9]。 多尺度运算是一个由粗到细的多层次描述和处理方法,如同人的感知过程,先通过对大范围特征进行粗分析,再通过捕捉细节使分析越来越精细,最后获得对感知对象的准确认识。在具体实施过程中,其采用不同尺寸的结构元素对信号进行变换。 假设给定了形态运算T和信号X,则基于T的多尺度形态学运算可定义为一族形态学变换{Tλ|λ>0},其中Tλ定义为 Tλ(X)=λT(X/λ),λ>0, (9) 式中:λ>0为刻度,即可推导出多尺度膨胀、腐蚀、开和闭运算分别为 (fΘg)λ(n)=fΘλg1/λ(n), (10) (f⊕g)λ=f⊕λg1/λ(n), (11) (f∘g)λ=f∘λg1/λ(n), (12) (f·g)λ=f·λg1/λ(n), (13) 式中:g1/λ(n)=g(n/λ)。若结构函数取凸函数,随着刻度的增大,多刻度运算会滤去信号更大的变化,使信号越来越简单。 将柔性形态学中的硬核A进行多尺度化,即实现了多尺度柔性形态运算,其膨胀和腐蚀分别定义为 {fΘ[B,A,k]}λ(x)=min(k){k<>λf(a/λ):a∈Ax}∪{f(b):b∈(BA)x}, (14) f⊕[B,A,k](x)=max(k){k<>λf(a/λ):a∈Ax}∪{f(b):b∈(BA)x}。 (15) 由此可推导出开运算和闭运算的表达式,这里不再赘述。MSMF对SMF中的核结构元素多尺度化使得形态运算更加灵活,从而达到进一步改善形态滤波器性能的目的。 在某型单级齿轮箱上进行试验验证。在该系统中,由电动机带动输入轴,输出轴带动负载。主动齿轮齿数Z1为30,被动齿轮齿数Z2为50,输入端滚动轴承型号为6206,局部损伤故障分别在钢球、内圈和外圈表面采用电火花机加工制作,损伤直径为0.178 mm。试验时采样频率fs为12 800 Hz,采样时长为1 s,转速为1 136 r/min,计算可得内圈故障的特征频率为102.5 Hz,外圈故障的特征频率为67.9 Hz,钢球故障的特征频率为89.2 Hz。 测得轴承故障信号的时域波形如图 1所示。图 2是对原始信号直接进行Fourier变换得到的频谱图,由图 2可知,轴承故障特征频率完全被噪声所淹没,无法诊断出任何故障。 图1 轴承3种故障的原始信号 图2 原始信号的频谱图 选择结构元素B的长度为20,A的长度为7,k为2,λ为2,取MSMF开和闭运算的平均值,滤波后的时域如图3所示,频谱如图4所示。由图4可知,经过MSMF滤波后,转频及内圈、外圈和钢球的故障特征频率及其倍频清晰可见,从而能诊断出轴承的3种故障。 图3 多尺度柔性形态滤波时域图 图4 多尺度柔性形态滤波频谱图 文献[1]给出了形态滤波解调和Hilbert变换解调比较结果,表明形态滤波解调和Hilbert变换解调相比能获得更好的信噪比,在此不再赘述。下文以外圈损伤为例对多尺度柔性形态滤波和柔性形态滤波的效果进行比较,对图 1b所示轴承外圈损伤信号进行柔性形态滤波,A,B,k的取值同上,取开运算和闭运算的平均值,滤波后的时域和频域如图5所示。 图5 柔性形态滤波效果图 由图5可知,柔性形态滤波同样能达到滤除噪声的目的,但是滤波后信号的幅值明显降低,说明柔性形态滤波在滤除噪声的同时也滤除了部分的冲击脉冲,且滤波后仍有较大噪声,这为进一步的故障诊断带来不便,相比之下,多尺度柔性形态滤波在滤除噪声的同时能更好地保留原始信号中的冲击成分,因此其滤波效果优于柔性形态滤波的滤波效果。 数学形态滤波作为一种很好的非线性滤波方法在机械故障诊断领域获得了越来越广泛的应用,但是经典的形态学滤波由于取单一结构元素,故在滤波效果上存在很大不足,常常会滤除对诊断具有很大价值的脉冲信号。柔性形态学在鲁棒性和保留细节方面对经典形态学做了改进,在此基础上,提出了一种基于多尺度的柔性形态滤波算法,该算法进一步优化了柔性形态运算中的结构元素,目的是更好地提取轴承故障信号的冲击脉冲。试验表明,多尺度柔性形态滤波在获得较高信噪比的同时,比经典的柔性形态滤波能够更好地保留故障轴承原始信号中的冲击成分。 除了形态算子的设计影响滤波效果外,结构元素、k和λ值的选择对结果的影响也较大,针对轴承振动信号如何选取适当的结构元素及其内核的大小以及k,λ值,以获得更好的处理效果,还有待进一步研究。2 多尺度柔性形态滤波
2.1 多尺度形态学
2.2 多尺度柔性形态滤波
3 在轴承故障诊断中的应用

4 与柔性形态滤波的比较

5 结束语
